Specific heat capacity questions and equation
Specific heat capacity questions and equation
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Specific heat capacity questions and equation
Whenever two objects with different initial temperatures are put in contact with each other, the warmer one will cool down, and the cooler one will warm up, until they reach the same temperature. We now know that this has to do with the motions of molecules: what we sense as temperature is related to the average kinetic energy of the molecules of each material: the faster they’re vibrating around, the hotter the object feels. We can sidestep this molecular picture by dealing with objects as a whole, and treating the energy transfer as the flow of heat, rather than kinetic energy transfer among particles.
Specific Heat for Various Materials |
|
Material |
Specific Heat |
Water |
4186 |
Aluminum |
900 |
Steel |
448 |
Brass |
386 |
Copper |
380 |
Experiments have shown that the heat transfer Q = mcΔT, where ΔT = Tfinal-Tinitial of the object you’re considering, m is its mass, and c is referred to as the “specific heat” of the material it’s made up of. For most materials over a wide range of temperatures, c is close enough to a constant value that we will consider it to be exactly constant. Note that a positive Q means that energy flowed into the object (raising its temperature), while a negative Q means that energy left the object (leaving it at a lower temperature than at the beginning). Also note that you must be careful to associate the mass, specific heat, initial temperature, and final temperature, for the appropriate object being considered in any particular calculation, and not some other object.
Energy is always conserved, and this is a useful fact when dealing with heat as a kind of energy flow. If we have a perfectly insulating container, then no energy can flow into or out of that container. So, the net heat flow for everything in the container combined Qnet must equal zero.
In this particular lab, we will heat up a metal sample, and drop it into a cooler inner calorimeter cup partially filled with water. We will assume that the rest of the calorimeter is perfectly insulating, so that:
Qnet = 0, or Qmetal + Qwater + Qcup = 0
If the cup were not perfectly insulating, we would also have to have a term for the heat transfer to the surrounding air, stirrer, outer cup, etc.
PROCEDURE
1. Gather all the necessary materials: triple-beam balance, metal samples, calorimeter cup, two temperature sensors or thermometers, metal can, and hotplate. Note: the temperature sensor that you use in your calorimeter must not have blue plastic tubing at the end, but the one you use to measure the temperature of the heated sample may or may not, it does not matter. In either case, never remove the blue plastic tubing from any temperature sensor.
2. Fill the metal can approximately half full of water and start heating it on the hotplate. Note: you want the water to be hot, but not boiling (60-80°C is a good temperature). Also: try to keep the temperature of the water as steady as possible, by keeping the hotplate on a constant setting, and stirring the water occasionally.
3. Measure the mass of the inner aluminum cup only (remove it from the outer cup, and remove the plastic ring) using the triple-beam balance. Note the uncertainty in this mass.
4. Note which metal sample you are using. Then, measure the mass of the metal sample using the triple-beam balance. Note the uncertainty in this mass.
5. Tie a thread to the metal sample, and lower the sample into the metal can, to allow it to heat up. (Keep the end of the thread outside, so that you may pull the metal sample out easily.) Insert a temperature sensor or thermometer into the water in the can, so that you will be able to measure its temperature.
6. At the sink, fill the inner aluminum cup part-way with cool water. You will want enough to completely cover the metal sample (when the sample is lying on its side), but not much more. If you use too much water, the temperature change will be too small to get reliable data. If you use too little, the metal sample will lose significant heat to the surrounding air, and it will be difficult to bring the cup, water, and sample into thermal equilibrium.
7. Measure the mass of the inner aluminum cup (still without the plastic ring), now partially filled with water. Note the uncertainty in this mass. The mass of the water itself will be this new mass, minus the mass you found in step 4.
8. Insert the inner calorimeter cup (now containing water) into the outer calorimeter cup, with the plastic insulating ring separating them. Place the cover over the calorimeter and insert the second temperature sensor or thermometer through the stopper in the top cover. The stirrer should also be inside, going through the hole near the middle of the top cover. Gently stir the water for about a minute.
9. Once the all temperatures are stable, record the initial temperature of the cool water in the calorimeter cup. We will assume that the aluminum inner cup is also at the same temperature. Also record the initial temperature of the metal sample, which we will assume is the same as the temperature of the water in the metal can on the hotplate.
10. Carefully remove the metal sample from the metal can, and quickly remove the cover from the calorimeter. Quickly place the metal sample in the inner calorimeter cup, and confirm that it is indeed fully submerged. Quickly re-cover the calorimeter. (Remember, we want no heat to escape to the outside air.)
11. Gently stir the water until the water and metal specimen reach a final equilibrium temperature. (You can confirm this by moving the temperature sensor around, looking for “hot spots” or “cool spots.” Generally, as long as your temperature sensor is not near a “hot spot,” the equilibrium temperature will likely be your highest reading. This is because the calorimeter is not actually a perfect insulator, so the heated parts will lose heat to the room, desk, etc.) Record the final equilibrium temperature, with its uncertainty. (Note: much of this uncertainty will be due to the fact that your “final” temperature is a judgment call, made when you guess that everything has first reached equilibrium.)
12. Repeat steps 4-11 for the remaining metal samples.
Source : http://www.personal.psu.edu/sac130/courses/labs/specific_heat.doc
Web site link: http://www.personal.psu.edu/
Author : not indicated on the source document of the above text
Specific Heat
In the model we developed in Dialog 3 to explain the results of mixing two samples of water, the warmer water and the cooler water had the same mDTs. The internal energy of the warmer water decreased and the internal energy of the cooler water increased. There was heat transfer, Q = mDT, from the warm water to the cooler water. If you look at the data tables from Exploration 4, you will notice that the mDTs of the metal samples were much greater than the mDTs of the water. Since the m DTs were different for the water and metal samples, our current model will not work to explain the results of mixing water with metal. The model we developed for water must be modified to account for materials other than water.
Water Equivalency
The model that explains the mixing of different materials at different temperatures uses a concept called water equivalency. To understand this concept, we will begin by reviewing Exploration 3. In Exploration 3 the same fluids were mixed at different temperatures, as shown in the diagram below.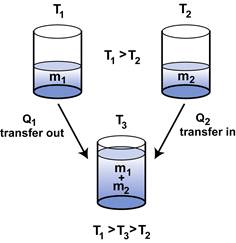
The final mixture was at a temperature, T3.
- The temperature T3 was less than T, so the mass of fluid, m1, had a reduction in its internal energy. Heat, Q1, transferred out of the fluid, m1.
- The temperature T3 was greater than T2, so the mass of fluid, m2, had an increase in its internal energy. Heat, Q2, transferred into the fluid, m2.
The Q’s can be represented by m DT. Since the system was isolated there was no energy exchanged with the environment. Therefore:
Q1 + Q2 = 0
m1 (T3 – T1) + m2 (T3 – T2) = 0
m2 (T3 – T2) = - m1 (T3 – T1) = m1 (T1 – T3)
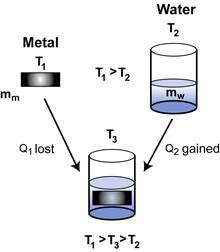In Exploration 4 a metal sample of mass mm and temperature T1 was added to water of mass mw and temperature T2. Pictorially, this can be represented as the diagram at right.
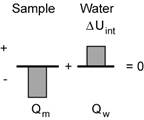
The physics representation says the metal sample lost heat and the water gained heat. But because the system was isolated, the energy gained by the water must equal the energy lost by the metal. The total internal energy content of the system must remain constant.
So far, everything is the same as the model developed in Exploration 3. However, when we compared 
(T1 – T3) to mw (T1 – T3) we found that they were not equal. Since the fundamental principle of energy conservation must apply, this means that there is something wrong with our mathematical representation: the formula mDT does not give us the right amount of heat transfer, Q, when we use a material other than water. We must modify this formula to account for different materials.
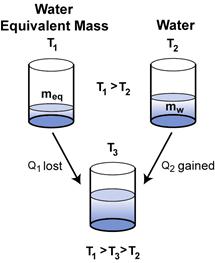The modification that we will use is based upon the concept of water equivalent mass. Pictorially, this concept can be represented as the diagram at right. This is the same as the pictorial representation for Exploration 4 except the metal sample has been replaced by the water equivalent mass. The initial temperatures of the water, T2, the water equivalent mass, T1, and the final temperature, T3, are the same as in Exploration 4. The mass of the initial water, mw, is also the same as in Exploration 4. The water equivalent mass, meq is what would cause the same change in temperature (T2 – T1) of the water, mw, that the metal sample, 
, caused.
To calculate the value of the water equivalent mass, meq , the model we used in Exploration 3, when two water samples were mixed, can be applied to our new model.
meq (T3 – T1) + mw(T3 – T2) = 0
From Exploration 4, the values of mw, T1,T2, and T3 can be substituted and meq can be calculated.
Hopefully, you now have a good understanding of the concept of water mass equivalent. In practice, water mass equivalent is usually not calculated. Instead another term, called specific heat, is used. This new quantity is called the specific heat, and is given the symbol c. Its numerical value is equal to the ratio of the water mass equivalent and the mass of the sample of the material:
.
With this new model the equation for heat transfer becomes
where ms is the mass of the sample.
Scientists commonly use two sets of units to express heat transfer, Joules and calories. The unit of specific heat, c, will depend on which one of these units is used:
- If heat is expressed in Joules, m will be measured in kilograms, and c is expressed as
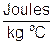. This is the amount of heat, Q (Joules) necessary to raise 1 kg of material 1o C. - If heat is expressed in calories, m will be measured in grams, and c is expressed as
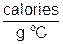. This is the amount of heat, Q (Joules) necessary to raise 1 gram of material 1o C.
The change in temperature, DT, is always measured in degrees Celsius. Because the values of specific heat for different materials are determined by a comparison to water, the specific heat of water is assigned a value of 1
.
When you use the heat transfer equation, Q = ms DT, it is important to note that heat transfer, Q, cannot be measured directly in the laboratory—only the temperature of an object can be measured. In our model, heat transfer in or out of the system is the way we explain temperature changes in our system. Heat has either flowed into or out of the object when its temperature changes.
Tables for the specific heat of common materials are shown below. Use the tables to solve the problems in this module.
Specific Heatof Common Substances |
|
||
Material |
calorie g oC |
Joule kg oC |
|
Ethylene Glycol |
0.57 |
2390 |
|
Acetone |
0.57 |
2390 |
|
Olive oil |
0.47 |
1970 |
|
Sulfuric Acid |
0.34 |
1420 |
|
Mercury |
0.033 |
138 |
|
Hydrogen |
3.4 |
14,246 |
|
Helium |
1.3 |
5450 |
|
Steam |
0.48 |
2010 |
|
Nitrogen |
0.24 |
1010 |
|
Air |
0.24 |
1010 |
|
Oxygen |
0.22 |
922 |
|
Carbon dioxide |
0.20 |
838 |
|
Argon |
0.125 |
524 |
|
Liquid Ammonia |
1.1 |
4610 |
|
Water |
1.00 |
4190 |
|
Alcohol (ethyl) |
0.58 |
2430 |
|
Specific Heatof Common Materials |
||
Material |
calorie g oC |
Joule kg oC |
Ice (at 0o C) |
0.5 |
2090 |
Wood |
0.42 |
1760 |
Earth (dry clay) |
0.22 |
922 |
Aluminum |
0.215 |
900 |
Stone (granite) |
0.19 |
796 |
Glass |
0.15-0.20 |
629-838 |
Iron (steel) |
0.107 |
448 |
Zinc |
0.093 |
390 |
Brass |
0.092 |
385 |
Copper |
0.0924 |
387 |
Silver |
0.056 |
234 |
Gold |
0.0308 |
129 |
Lead |
0.0305 |
128 |
Tin |
0.055 |
230 |
The ratio of the mass of the water equivalent mass of the metal is numerically equivalent to the specific heat. The specific heat compares the amount of water it
would take to cause the same temperature change as the given substance. For example, consider steel, which has a specific heat of 0.107 
. This value tells us that if a mass, ms, of steel causes a certain temperature change then 0.107 ms of water will cause the same effect. Conceptually, you can think of specific heat as the amount of energy transfer that will cause the temperature of 1 g (or 1 kg, if the heat is measured in Joules) of a material to change by 1 oC – look at the units of the specific heat to see that this is so.
Compare the ratios for the steel and the aluminum samples you calculated in Exploration 4 to the values of specific heat in the table.
Steel Aluminum
Your calculated value = _______ Your calculated value = _______
Value in the table = __________ Value in the table = __________
Percent difference = _________ Percent difference = _________
Most likely, the values you obtained from your experiments in Exploration 4 are not exactly the same as the values in the table. You can expect some disagreement between your values and those in the table because the Styrofoam cup you used was not a completely isolated system. Also, the thermometer introduced error not only because of the difficulty of reading it to a precision of more than 0.1 oC, but also because there was heat transfer to the thermometer that was not taken into account. You should not be concerned if your measured value for the specific heats was not exactly the same as those in the table. The procedure in Exploration 4 was not intended to result in an accurate value of c; rather, it was intended to show you the necessity of specific heat and the general procedure scientists use to find it.
Problem Solving Strategies
In previous modules, we presented a strategy to guide you in developing your problem solving skills. This strategy can work in a wide variety of situations in both science and technology because it shows various representations. You will use same strategy in this module:
- Sketch the situation. This sketch will be the real-world representation. Identify the system or object and circle the system with a dotted line, if possible.
- Draw an energy bar diagram to show the physics representation.
- List the given and unknown information about the situation, and identify the initial and final situations.
- Develop or select equations to describe the situation for the mathematical representation.
- Solve the problem and check that the result is reasonable, has correct units, and answers the original question.
Example 1
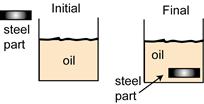
A technician drops a steel part at 700o C into an oil bath (c = 0.5
) during a quenching process. The oil bath must operate between 25o C and 30o C, but the technician needs to use the smallest amount of oil possible. If the oil is initially at 25o C, how much oil is required to quench a 175 g steel part?
Solution
Real-world representation (sketch):
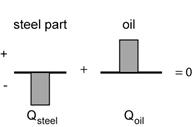
Physics representation (energy bar diagram):
Givens: Oil: c = 0.5
Steel: c = 0.107
Steel: m = 175 g
Unknown: Oil m = ?
Initial conditions |
Final conditions |
Steel part Ti = 700o C |
Steel part Tf = 30o C |
Mathematical representation: Qsteel + Qoil = 0 Q = mcΔT
Solve the problem:
Example 2
A technician needs to determine the amount of energy required to increase the temperature of a vat containing 12 kg of water. The water enters the vat from the water mains at a temperature of 15o C. The technician knows that the final temperature required is 90o C. How much energy is required, in Joules and in calories, to raise the temperature of the water from 15o C to 90o C?
Solution
This problem is a little different from the previous example. In this case the water is not an isolated system; it is getting an input of energy from the environment. But if we consider the environment to be part of the system, conservation of energy still applies. The energy lost by the environment must equal the energy gained by the water.
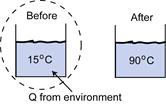
Real world representation (sketch):
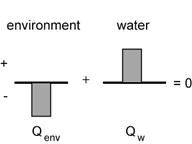
Physics representation (energy bar diagram):
Givens: Because the mass of water is given in kilograms, we will use the specific heat for water in units that include kg.
mw = 12 kg Water: c = 4190 
Unknown: Q = ?
Initial conditions |
Final conditions |
Ti = 15 oC |
Tf = 90o C |
Mathematical representation: Qenv + Qwater = 0 Q = mcΔT
Solve the problem:
The negative sign indicates that the environment lost energy. The heat gained by the water is Q = 3.77x106 J. To determine the amount of energy in calories, we use the conversion from the chart in Dialog 3:
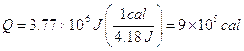
Source : http://physics.mtsac.edu/2A/Modules%20Master/6%20Heat%202005%20revised.doc
Web site link: http://physics.mtsac.edu/
Author : not indicated on the source document of the above text
Specific heat capacity questions and equation
Episode 607: Specific heat capacity
Energy must be supplied (or rejected) to increase (or decrease) the temperature of a material. Here is how to calculate how much.
Summary
Discussion: Energy and change of phase. (15 minutes)
Student experiment: Measuring specific heat capacities. (40 minutes)
Worked example: Calculation involving c. (10 minutes)
Student questions: Calculations. (30 minutes)
Discussion:
Energy and change of phase
Up until this point the link between ‘internal energy’ and temperature has been qualitative, except for gases. In order to extend the discussion to solids and liquids we need to get more quantitative in two ways. One is to discuss how much the temperature of a body changes when its internal energy in increased by a certain amount. The other is to ask what happens when a substance changes phase from a solid to a liquid or liquid to a gas.
Start by introducing the equation for specific heat capacity c (SHC) and defining the terms. The word specific is an old fashioned way of saying ‘per unit mass’. Work through a simple calculation.
Understanding this equation will help solidify ideas about temperature and energy and how they differ. A possible analogy was supplied by Richard Feynman. He suggested thinking of heat energy as being like water, and temperature as wetness. A towel can have different amounts of fluffiness, so take more or less water to make it wet. When we dry ourselves, we dry until the towel is as wet as we are (“same temperature”).
The anomalously large SHC of water should also be discussed as it is particularly important for the development and maintenance of life on Earth.
NB nomenclature: there isn’t any agreed way to name c. Some use specific thermal capacity, others favour specific heating capacity to emphasise the fact that ‘heat’ is not an entity but a short hand name for a process (heating as oppose to working). Perhaps the most common is specific heat capacity.
Another source of confusion is treating state and phase as synonyms (as in changes of state / phase). Solids, liquids and gases are three of the different phases of matter (superfluids and plasmas are two others. NB Here, by a plasma, we mean an ionised gas, not a biological fluid). Thus melting, boiling etc are changes of phase. Each phase can exist in a variety of states depending upon e.g. the temperature and pressure. Thus the Ideal Gas Equation of State
PV = nRT summarises the physically possible combinations of P, V and T for n moles of the ideal gas.
Student experiment:
Measuring specific heat capacities
Students should carry out an experiment to measure the specific heat capacity of a solid and/or a liquid very soon after meeting the expression. There are a number of points to note here:
- If specific heat capacity is constant, the temperature will rise at a uniform rate so long as the power input is constant and no energy is lost to the outside.
- There are large potential heat losses if the substance is not well insulated. These can be accounted for but in most cases students will not do so quantitatively.
- They should calculate their value and make a comparison with data book values. They should be able to think of a number of reasons why their value does not match that in the data book.
Several different methods of determining the SHC of liquids and solids are given in the links below. Choose those best suited to your pupils and available equipment.
TAP 607-1: Measuring the specific heat capacity of a metal
TAP 607-2: The specific heat capacity of water and aluminium
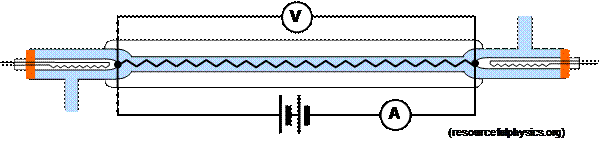
It is useful to compare electrical methods of measuring the specific heat capacity of a solid and liquid including the continuous flow calorimeter for a liquid.
TAP 607-3: Measurement of specific heat capacities
Worked example:
Calculation involving C
This example deals with the mixing of liquids at different temperatures.
1.5 l of water from a kettle at 90°C is mixed with a bucket of cold water (10 l at 10 °C) to warm it up for washing a car. Find the temperature of the mixed water, assuming no significant heat loss during the mixing. c of water = 4.2 kJ kg-1 °C -1
Answer: If there is no heat loss and no work done then the total energy of the system at the end is the same as at the start. Working with temperature differences from 10°C we have:
Initial energy = m c DT = 1.5 ´ 4200 ´ (90-10) [as 1.5 l has mass 1.5 kg] = 504 kJ
This is the amount of energy available to raise the temperature of all 11.5 l of water. Hence:
504 ´ 103 = 11.5 ´ 4200 ´ (T-10) [where T is the final temperature]
T = 20.4°C.
You can invent similar problems using a mixture of substances – a hot brick in water for example. However, be careful to consider realistic situations where not too much is lost as steam.
Student questions:
Calculations
A range of questions involving specific heat capacity.
TAP 607-4: Specific heat capacity: some questions
TAP 607-5: Thermal changes
TAP 607- 1: Measuring the specific heat capacity of a metal
The value of the specific thermal capacity of a material tells us how much energy is needed to change the temperature of one kilogram of the material by 1 degree. It is an important measurement for engineers and physicists who work with any material that changes its temperature or is designed to retain thermal energy.
In this activity you will make measurements to calculate a value for specific thermal capacity and consider some of the uncertainties in the measurements you have made.
You will need
- 1 kg blocks for thermal capacity
- 12 V immersion heater (typically 60 W)
- thermometer, 0 – 100 °C
- power supply, 0 – 12 V rated to supply 6 A
- 4 mm leads
- two digital multimeters
- stopwatch
Basic experiment
- Insert a thermometer and the immersion heater into their respective holes in the block. You may wish to drop a small amount of oil into the thermometer hole to improve the thermal contact between thermometer and block.
- Allow the thermometer to reach thermal equilibrium and then write down the temperature.
- Set up a suitable circuit that will enable you to measure the energy input to the heater.
- Turn on the current, noting the time if you are measuring energy using an ammeter and a voltmeter to record power.
- Energy = current ´ potential difference ´ time. Monitor and note the meter readings as the energy is supplied. They may change slightly as things warm up.
- Allow the block to heat up by about 10 °C, then turn off the current and note the time again.
- At this point, keep watching the thermometer. The temperature at the turn-off time is not the appropriate final temperature to record. What do you think is the appropriate final temperature?
- Use DE = m c Dq to calculate the specific thermal capacity, c, of your block. Compare your answer with a data book value.
- Was your calculated value of specific thermal capacity too high or too low? Which of the measurements you made is likely to be the one most in error? In which direction is it in error, and why might this be?
Slightly more sophisticated…
Energy losses are a problem in this experiment. The electrical energy measured going into the heater does not correspond exactly to the thermal energy actually delivered to the block itself (some of it goes to the immersion heater and to the surroundings) and so the temperature will increase less than you expect.
As a first improvement to the basic method, try cooling the block to about 5 °C below room temperature (stand it in cold water for a while) and then warm it to about 5 °C above room temperature.
Did this improve your value? How does this method help to reduce heat losses?
Outcomes
- This experiment gives you a value for the specific thermal capacity of a metal. If others in your group have used different metals, compare your values. You may also have evaluated the specific thermal capacity for water. Is this value very different?
- You have considered energy losses in this experiment and you may have worked hard to remove them. Generally, when devising your own experiments, try to be ingenious in removing or reducing unwanted effects.
Safety
Check the seals on the immersion heaters before use. Reject any that are obviously defective. In doubtful cases, any water which has entered during a precious activity can be removed by placing the heater in an oven for an hour at about 80 °C.
Practical advice
If you can provide a selection of different metals, it might be interesting to ask groups of students to use different blocks in order to compare results. The activity here assumes the use of an ammeter, voltmeter and stop-clock. Students using a joulemeter need only to take initial and final readings.
Some may still find setting up the electrical circuit demanding, and may need support.
It may be that the greatest source of error in this experiment is the lack of a smooth power supply. The meters do not read the correct average value of dc+ heavy ripple. If high current smoothing units are available they should be used. Better still would be 12 V car batteries.
Be safe
Impress on students the need to avoid running the immersion heaters outside the blocks, and not to cool them in water when hair-line cracks will draw water inside.
If 12 V car batteries are used, remember that they are often too heavy for one technician to lift.
Alternative approaches
A number of approaches may be used here depending on the abilities of the students. Certainly you should not feel constrained to use the proprietary blocks and immersion heaters if other equipment is already available. It might be possible with an able group to introduce a method of mixtures variant as a final piece of extension material but this would need careful treatment with a simpler method first.
Social and human context
The specific thermal capacity is an essential quantity to consider for any change of temperature. When materials are used for cooling purposes, for example, it is crucial to remove energy quickly and economically without the coolant changing its temperature too greatly. Water is, of course, ideal in this respect. But other materials are used too. In nuclear reactor technology, a variety of coolants are used to remove thermal energy from the reactor core, including liquid sodium. An additional property for reactor coolants is that they should not disturb the running of the reactor by absorbing neutrons. Hot water, close to boiling, when dropped on to the skin can cause great harm. It releases large quantities of energy into the tissues and, as every first-aider knows, the correct remedial treatment is to cool the affected part (i.e. to remove thermal energy from it) for a time of at least 500 s. This removes thermal energy from the underlying tissue as well. Storage heaters rely on the large mass and the high specific thermal capacity of the hot materials; the heater needs to retain the energy for a significant time for release into a room late into the day.
External reference
This activity is taken from Advancing Physics chapter 13, 220E
TAP 607- 2: The specific heat capacity of water and aluminium
This experiment is designed to measure the specific heat capacities of water and aluminium.
Before starting the experiment read through the instructions carefully.
You will need:
- 12 V immersion heater 60 W
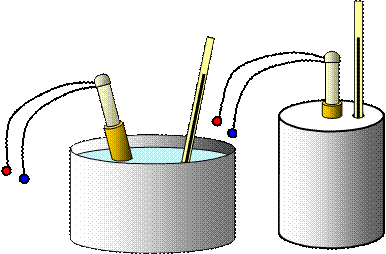aluminium saucepan- 1 kg block of aluminium
- thermometer
- 12 V power supply (6 A)
- stop clock
- balance
- 2 digital multimeters
What to do
1. Water
Put 1 kg of water in the saucepan and measure its temperature. Now hold the heater in your hand and switch on the power supply. When you feel the heater getting warm put it in the water and start the stop clock. After 10 minutes switch off the power supply, stir the water and take its temperature. Allow the heater to cool in air.
2. Aluminium
Put the thermometer in the small hole in the aluminium block. Switch on the heater and when it is warm put it in the large hole in the block and start the stop clock, having recorded the initial temperature of the block. After 10 minutes switch off the power supply and take the temperature of the block.
Safety
Check the seals on the immersion heaters before use. Reject any that are obviously defective. In doubtful cases, any water which has entered during a precious activity can be removed by placing the heater in an oven for an hour at about 80 °C.
Measurements to make
Mass of water (m) = kg
Temperature of water before heating = oC
Temperature of water after heating = oC
Rise in temperature of water (q) = oC
Voltage applied to heater (V) = V
Current through heater (I) = A
Electrical energy converted to heat energy in 10 minutes = J
Heat energy required to heat m kg by q oC = J
Specific heat capacity of water = J / (kg oC)
Make up a similar set of results for aluminium.
Questions
- Why do you think that you allowed the heater to warm up before putting it in the water?
- Why will your result for either experiment not be very accurate?
- Why should you stir the water at the end?
- Why would it not be a good idea to get the water or aluminium too hot?
Follow up topic
Devise an experiment to measure the specific heat capacity of soil.
Practical advice
After switching off the heater make sure you take the highest temperature reached by the thermometer in the aluminium block.
External reference
This activity is taken from Resourceful Physics
TAP 607- 3: Measurement of specific heat capacities
There are several simple methods for measuring the specific heat capacities of both solids and liquids, such as the method of mixtures, but we will consider here only electrical methods. Since the specific heat capacity varies with temperature, we have seen it is important to record the mean temperature at which the measurement is made.
Electrical calorimeters
Figure 1(a) and 1(b) show possible arrangements for electrical calorimeters for a solid and a liquid specimen.
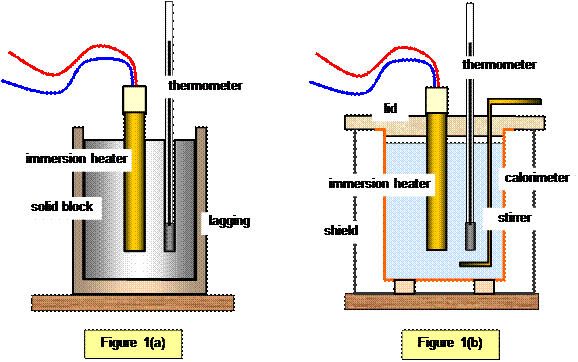
The material under investigation is heated by an electrical immersion heater and the input energy (Q) and the rise in temperature that this produces are measured. If the mass of the specimen (solid or liquid) is m and its specific heat capacity C, then:
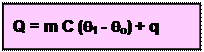
where θ0 and θ1 are the initial and final temperatures of the specimen and q is the heat loss. Using the cooling correction, the value of q may be found. This simple method can be used for liquids or solids, although in the case of a liquid, allowance has to be made for the thermal capacity of the container, and the liquid should also be stirred to allow an even distribution of the heat energy throughout its volume. This is necessary since liquids are such poor thermal conductors
The continuous-flow calorimeter
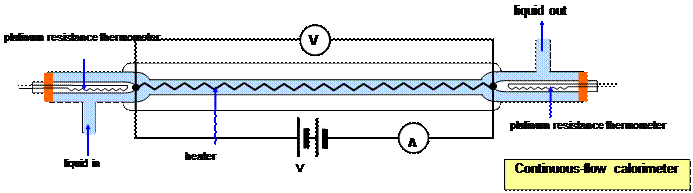
This was first developed by Callender and Barnes in 1902 for the measurement of the specific heat capacity of a liquid, and is shown in diagram below. Its main advantage is that the thermal capacity of the apparatus itself need not be known.
Liquid flows in from a constant-head apparatus at a constant rate past a thermometer (θ 0). It then flows around the heater coil and out past a second thermometer where the outlet temperature (θ1) may be measured. When steady-state conditions have been reached (a temperature difference between inlet and outlet points of 50C is reasonable) the temperatures and the flow rate of the liquid (m) are measured. A vacuum jacket round the heater coil reduces heat losses.
The electrical energy supplied to the heater coil (E = V I t) may be found readily with a joulemeter or with an ammeter and voltmeter.
Two sets of measurements are carried out.
For a first experiment we have:
Electrical energy supplied (E1) = V1 I1 t1 = m1 C (θ1 – θ0) + q
C is the specific heat capacity of the liquid and q the heat loss to the surroundings and to the apparatus.
The flow rate and rate of energy input are now altered to give a second set of results. However, if the inlet and outlet temperatures are the same as in the first experiment the heat loss will also be the same. Therefore:
Electrical energy supplied (E2) = = V2 I2 t2 = m2 C (θ1 - θO) + q
Eliminating the heat loss (q) gives
Practical advice
A smaller amount of water could be heated in a polystyrene cup than in a calorimeter; this reduces the heating time needed and provides insulation. The heater must be covered by the water. The heat absorbed by the polystyrene is also small compared to that absorbed by the calorimeter. However take care that the heater does not touch the cup or it will melt. Thermometers can also overbalance the cup. Always stir liquids before taking a temperature.
It is better to choose an immersion heater that fits all the way into the solid material rather than having part of it in the air. The top of the block should also be lagged. Take the highest temperature reached by the block after the heater has been switched off.
External reference
This activity is taken from Resourceful Physics
TAP 607- 4: Specific heat capacity: some questions
What to do
Three of these questions ask you to consider areas in which specific heat capacity is important: one domestic, one transport-based and one industrial. The remaining questions are calculations that involve the use of specific heat capacity.
The specific heat capacity of water is 4200 J kg–1 K–1; the specific heat capacity of air is about 1000 J kg–1 K–1.
Why does heat capacity matter?
1. Some cooks make toffee. Essentially, this is a process of boiling down a sugar solution to concentrate it and then allowing the liquid to cool until it sets. Small children are usually warned not to touch the cooling toffee for a very long time – much longer than the cooling for the same volume of pure water in the same vessel. Why is the cooling period so long?
2. Why is water commonly used in the cooling system of a motor car? Why is the system pressurised?
3. Find out which materials are used as coolants in nuclear reactors. What do these materials have in common?
Calculations
4. The Sun delivers about 1 kW of power to a square metre of the Earth when overhead at the equator. A parabolic mirror of radius 1m is used to focus this energy onto a container of water. Estimate the time taken by the mirror to raise 1 litre of water to 100 oC. Comment on whether your answer is likely to be an over or an underestimate.
5. Estimate how much energy is required to heat the air in your physics laboratory from a chilly 10 °C to a more comfortable 20 °C. Comment on the answer.
Practical advice
Students may find it more difficult to answer the qualitative questions than the quantitative questions. Answering qualitative questions provides essential practice in using the language (and concepts) of physics correctly.
Answers and worked solutions
1. There are a number of factors that determine the time it takes the toffee to cool sufficiently to eat:
The boiling point of the sugar solution is higher than that of water so the toffee is cooling from a higher temperature.
The sugar solution has a higher specific heat capacity than pure water. So for an equivalent temperature drop, more energy has to be lost.
[Perhaps most significant is the amount of energy that has to be lost for the liquid toffee mixture to solidify, cooling and then changing from a liquid to a solid takes a long time. This involves the idea of latent heat capacity, rather than specific heat capacity]
2. The specific heat capacity of water is large; water is cheap and liquid, it has a reasonable temperature range before boiling. It is pressurised to elevate the boiling point – but, as important, also to retain the material.
3. Coolants used include: water, heavy water (D2O), liquid sodium, pressurised carbon dioxide. They need a high specific heat capacity and, ideally, should not absorb neutrons.
Area of mirror is about 3 m2. So 3 kW is delivered. One litre has a mass of 1 kg, assume an 80 degree temperature rise.
Minimum time taken is (4200 J kg–1 °C–1 ´ 80 °C) / 3000 kg = 112 s but this does not allow for losses to the surroundings from the container which the Sun has to make up. This is an estimate of the energy needed to raise the temperature to 100 °C, it does not boil the water. Assuming no energy losses, it takes a further 800 s (minimum) to vaporise the liquid. An equally valid estimate – this time experimental – is to time your household kettle having read its electrical energy input from the base plate and then scale up or down its time to boiling accordingly.
5. Assume the laboratory is 3 m ´ 10 m ´ 10 m, this leads to a volume of 300 m2. Assume further that the heating is just a question of warming up the air. The density of air is approximately 1 kg m–3 so energy = 300 kg ´ 1000 J kg–1°C–1 ´ 10°C, i.e. 3 MJ.
A reasonable heater might deliver this in 1000 s (about 20 minutes). Most people would guess that the heating time would be much longer. This estimate ignores heating the contents of the room, etc. Our perception of temperature is affected both by the humidity of the air and by the cooling effect of any draughts. It would take much longer in reality.
External reference
This activity is taken from Advancing Physics chapter 13, 110S
Use these data to answer the questions below, showing how thermal changes apply to a wide range of phenomena:
Material |
Specific heat capacity / |
Aluminium |
900 |
Copper |
385 |
Expanded polystyrene |
1300 |
Iron and steel |
450 |
Ice |
2100 |
Air |
1000 |
Water |
4200 |
A set of varied questions
For each of the following, find the internal energy difference for a 10 K change in temperature:
1. 5.0 kg of water.
2. The bit of a soldering iron, made from 3.5 g of copper.
3. An expanded polystyrene cup of mass 5.0 g.
4. A steel brake disc of mass 1.5 kg.
5. If you eat a fruit pastry fresh from a hot oven, the pastry may be harmless while the fruit filling scalds your tongue.
Use your ideas about specific heat capacity to explain why.
6. You can put your hand in an oven at 200 °C and even touch a baking cake, without serious harm. But you must avoid touching anything in the oven made from metal.
Why is it not so harmful unless you touch metal?
7. In Fiji, some people will walk barefoot over a bed of white-hot pumice coals as part of a religious ritual. It is meant to demonstrate supernatural powers over pain and heat. Their feet are generally not hurt.
Pumice has a low specific heat capacity, low density and is a poor conductor of heat. Explain how each of these properties helps to make a bed of white-hot pumice coals safe to walk (quickly) over.
8. In the middle of the nineteenth century, James Joule performed a great series of experiments, which was part of the work leading to the law of conservation of energy. One of them was on his honeymoon, when he measured the temperature difference between water at the top and bottom of a waterfall.
If the waterfall was 100 m high, what maximum temperature difference could Joule expect?
Two holes are made in a 1.0 kg block of aluminium. A 48 W electric immersion heater is placed in one hole, and a thermometer in the other. Both objects make good thermal contact with the block. The heater is switched on for exactly 3 minutes and the temperature rises from 20 °C to 29 °C.
9. Calculate the specific heat capacity of aluminium.
10. Is this likely to overestimate or underestimate the true value?
In some supermarkets the freezer compartments are upright, with front-opening doors, while in other supermarkets there are chest-type freezers, with access from the top and no lids. Some people consider the upright design wasteful, because the cold air escapes when the door is opened. The temperature inside such freezers might be – 20 °C, and the specific heat capacity of air (at constant pressure) is about 1000 J kg–1 K–1.
11. Consider a freezer of volume 1.5 m3 and discuss whether you agree or disagree.
A power station needs to get rid of energy at a rate of 800 MW and does so by warming up a river that flows past it.
12. If the river flow rate is 1100 m3 s–1, how much warmer is the river downstream of the power station?
Practical advice
Students may find it more difficult to answer the qualitative questions than the quantitative questions. Answering qualitative questions provides essential practice in using the language (and concepts) of physics correctly.
Answers and worked solutions
1.
2.
3.
4.
5. The fruit, largely sugar and water, has a high heat capacity and therefore has more energy.
6. Both air and cake have low specific heat capacities and are poor conductors, so little energy is transferred; metals have higher specific thermal capacities but are good conductors, so the energy can be rapidly conducted to your hand.
7. Low specific heat capacity and density mean little energy is stored in the pumice; because it is a poor conductor, there is little energy transfer from below the surface.
8.
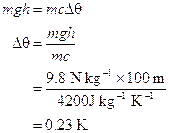
9.
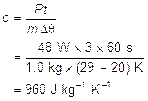
10. Overestimate. Because of thermal transfer to the surroundings, less energy goes into the aluminium than this calculation assumes.
11. Assume the freezer volume is half air (the other half is the contents of the freezer) and that all the air escapes when the door is opened. If the room temperature is 20 °C, the temperature difference is 40 K:
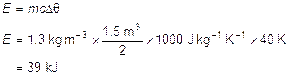
If the door were opened frequently, the power demand would be significant. But perhaps this is a contribution to the air-conditioning of the supermarket?
12.
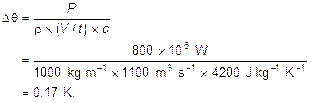
External reference
This activity is taken from Advancing Physics chapter 13, 140D
Source : http://tap.iop.org/energy/thermal/607/file_47502.doc
Web site link: http://tap.iop.org
Author : not indicated on the source document of the above text
Heat Capacity and Specific Heat
Consider a chunk of matter, which might be solid or might be a “parcel” of water or gas. Either way, we’ll call it an “object”.
The heat capacity of the object is a measure of how much heat the object must gain or lose to change its temperature by a given amount. In the MKS system, heat capacity would be expressed in units of Joules per degree Centigrade (°C)—that is, the heat capacity of the object would be the amount of heat (in Joules) that the object would have to gain or lose for its temperature to change by 1°C. Another common unit of heat capacity is the calorie per °C, where one calorie is defined as the amount of heat required to raise the temperature of 1 gram of pure water (at 3.98°C, 14.5°C, or 19.5°C, depending on who’s doing the defining) by 1°C at standard sea level pressure.
What determines an object’s heat capacity? One obvious answer is the amount of matter in the object (expressed in terms of its mass). The more “stuff” there is in the object—that is, the greater its mass—the more heat it would have to gain or lose for its temperature to change by 1°C. For example, it would take a lot more heat to warm the Pacific Ocean by 1°C than it would take to warm a glass of seawater by 1°C!
The other answer is that the heat capacity depends on the type of material of which the object is composed—not all materials require the same amount of heat gain or loss to change temperature by 1°C. That is, to change temperature by 1°C , objects made of some materials require a greater gain or loss of heat than do objects made of other materials, even when the objects have the same mass. For example, liquid water turns out to be one of the hardest substances to warm up or cool off in nature—it requires a greater gain or loss of heat to change its temperature by 1°C than the same mass of most natural substances on earth.
Heat capacity might depend on other things, too, such as the temperature of the object or the atmospheric pressure. For a gas, heat capacity would depend on whether pressure were being held constant during the heat gain or loss, or whether the volume were held constant, or neither.
A relation between the heat gained or lost (DQ) by an object and the change in temperature it undergoes can be written:
where 
is the object’s heat capacity (which depends on the various things described above).
The specific heat of a material is related to heat capacity, except that specific heat doesn’t depend on an object’s mass, though it still depends on the type of material. Specific heat is therefore a property of the material.
Specific heat is defined as the amount of heat that a unit mass of a material must gain or lose to change its temperature by a given amount. In MKS units it would be expressed in terms of Joules per kilogram per °C. A common alternative unit is calories per gram per °C. By definition of the calorie, the specific heat of pure water is 1 cal/gm/°C (at 3.98°C, 14.5°C, or 19.5°C, depending on who’s doing the defining) at standard sea level pressure.
The specific heat of a material is related to the heat capacity of an object made of that material as follows:
where 
is the specific heat and m is the mass of the object. Substituting into the earlier relation above, we derive a relation between the heat gained or lost by an object, the object’s mass, its specific heat, and its change in temperature:
We will take advantage of this relation to estimate the specific heat of sand, which we will take to be broadly representative of the specific heat of “land” on earth.
Measuring the Specific Heat of Sand
Given that the specific heat of water is 1 calorie/gm/°C (which we will take to be representative of sea water and hence “ocean”), we can measure the specific heat of sand (which we will take as representative of “land”) using the experimental procedure described below.
Materials Needed
-- thermos or other insulated container --beaker
-- thermometer -- weighing scale
-- water -- hot plate
-- sand
Procedure
(1) Record the temperature of the room in degrees centigrade. (This should also be the initial temperature of the sand, Ts(t0), assuming that the sand has been sitting around in the room sufficiently long.)
(2) Place the thermos on the scale and record its mass in grams.
(3) Add water to the beaker (no more than half full), place the beaker on the hot plate, and heat the water to a temperature lower than the maximum temperature measurable by the thermometer.
(4) Pour heated water into the thermos (no more than half full) and record its mass. Subtract the result of (2) from the result of (4) to determine the mass of water in the thermos, mw.
(5) Record the temperature of the water, Tw(t0), when the temperature has largely stabilized (or is changing only very slowly).
(6) Add sand to the water in the thermos (less than one quarter of the total volume of the thermos). Record the mass of the partly filled thermos and subtract the mass measured in (4) to determine the mass of sand, ms, added to the thermos.
(7) Cover the top and swish the sand around in the water briefly. Repeatedly record the temperature of the water/sand mixture and swish it around, until the temperature has largely stabilized. We’ll call this the “final” temperature, T(tf). It should be the temperature of both the sand and the water.
The Calculation
The calculation of the specific heat of the sand hinges on several assumptions, some better than others:
- When the approximately room-temperature sand is added to the heated water, the sand will warm and the water will cool by conduction, and the amount of heat lost by the water will equal the heat gained by the sand. No significant amount of heat is lost by the heated water to the thermos, the thermometer, or the air (by conduction or evaporation).
- The sand and water end up at the same temperature.
- The sand consists of material that all has the same specific heat.
The relations between temperature change and heat lost by the water and gained by the sand can be written separately as:
(1) 
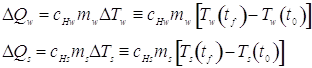
where 
and 
are the specific heats of water and sand, respectively. By assumption, the heat gained by the sand equals the heat lost by the water:
(2) 
Substituting Eqs.(1) into Eq.(2) to eliminate the heat gain/loss terms gives:
(3) 
The assumption that the sand and water end up at the same temperature can be written as:
(4) 
Substituting Eq.(4) into Eq.(3) gives:
(5) 
We have measured or otherwise know everything in Eq.(5) except 
, so we can solve for it:
(6) 
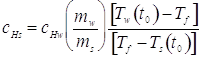
So, based on your measurements, how does the specific heat of “land” compare to the specific heat of “ocean”?
(The actual specific heat of quartz sand is 0.19 cal/gm/°C, though for sandy clay, which is more like soil, it’s 0.33 cal/gm/°C.)
Source : http://funnel.sfsu.edu/courses/gm310/F05/handouts/SpecificHeat.doc
Web site link: http://funnel.sfsu.edu/
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Specific heat capacity questions and equation
Specific heat capacity questions and equation
Specific heat capacity questions and equation
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does specific heat capacity mean ? Which is the meaning of specific heat capacity ?
Specific heat capacity questions and equation physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us