Buoyancy formula definition factor notes
Buoyancy formula definition factor notes
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Buoyancy
AP Physics - Buoyancy
Why do your basic massively heavy humungous ships float? An aircraft carrier weighs almost a hundred thousand tons. So why don’t it sink like a stone?
Aristotle thought it was due to the shape of a body. If the body had sharp edges, it would sink. If the body was smooth and rounded – like the hull of a ship – it would float. (So why do you have all those round rocks on the bottom of a river?)
Like most of the teachings of Aristotle, this is pure nonsense. The guy who actually figured out why things float was another Greek genius, Archimedes (ca. 287 – 212 B.C.). He discovered how buoyancy works. Buoyancy is an upward force that a fluid exerts on an object that is immersed in it. It causes things to float or else results in an apparent loss of weight of a body when it sinks in the fluid. This is called the buoyant force.
The important physics law dealing with buoyancy is called Archimedes' Principle.
Archimedes’ Principle º An object is buoyed up by a force equal to the weight of the fluid it displaces.
This rule is true both for gases and liquids, since they are both fluids.
Archimedes' lost principle º When a body is immersed in water, the phone rings.
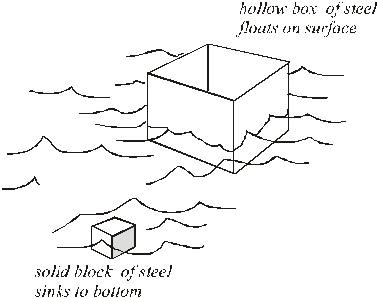Floating and Sinking: You have 2 tons of steel. Steel is 9 times denser than water, so the 2 tons of steel will only displace about 2/9 or 0.22 tons of water. The buoyant force is not nearly enough to float the block, so it will sink.
We now take the same 2 tons of steel and make a box from it. This hollow box has a much greater volume than did the cube. When you set the box in the water, is displaces a larger volume of water than the cube did, it is the displaced volume of fluid which creates the buoyant force. As the box sinks deeper into the water, it displaces more and more water, which causes the buoyant force to increase. When the buoyant force is equal to the weight of the box, it stops sinking and floats. The weight of the box is equal to the buoyant force so the net force on the system is zero.
So if the box is big enough, it will float.
As cargo ships are loaded with freight, they sink deeper into the water. As they sink deeper, they displace more water. This increases the buoyant force. The boat’s weight and the buoyant force or at equilibrium. The upward buoyant force is equal to the weight of the ship. As long as the total weight of the ship does not exceed the weight of the water displaced, the ship will float.
 |
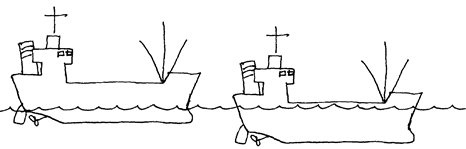Empty Ship Loaded Ship
Buoyancy In Air: Air is a fluid and Archimedes' principle applies to it just as it does to liquids.
An object surrounded by air is buoyed up by a force equal to the weight of the air displaced.
Balloons and blimps float in air just as boats float on water. A cubic meter of air has a mass of around 1.2 kg, so its weight is around 12 N. Thus any object that has a volume of one cubic meter and a weight less than 12 N would float, i.e., rise. If it weighs more than 12 N, it would sink, i.e., fall.
When you built a hot air balloon in chemistry, you took advantage of Archimedes' principle, even though you were thinking in terms of volumes and numbers of moles and all that ever so exciting chemistry stuff.
|
Imagine the blimp taking pictures of the superbowl as a large fish swimming in water. They both maintain their 'altitude' by controlling their density and taking advantage of Archimedes' principle.
Cause of the Buoyant Force: You toss a rock into the water and it sinks. The forces exerted by the pressure of the water act perpendicularly to the outer surfaces of the rock (Pascal’s principle).
Let’s look at the forces.
The horizontal forces pushing in on the sides cancel each other out.
This does not happen with the vertical forces. As the depth increases, the pressure increases. This means that the forces pushing up, on the bottom of the rock, are greater than the forces pushing down on the top of the rock. This is because the bottom of the rock is at a greater depth than the top of the rock, so the pressure is greater. Recall that 
, so the greater the depth the greater the pressure.
The difference in the forces on the top and bottom are responsible for the buoyant force.
Finding the Buoyant Force: A cube with area A on all its sides is immersed in a fluid.
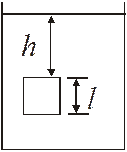We can find the force pushing down on the top. We can also find the force pushing up on the bottom surface of the cube:
so 
We also know that 
We can plug that into the force equation we just developed:
Force on top: 
Force on Bottom: 
gis the acceleration of gravity. l is the length of each side of the cube. his the depth of the top of the cube.
The force on the bottom is greater than the force on top, the difference is the buoyant force. We can find this difference:
The area of the cube A multiplied by length of the cube’s side l is the volume of the cube, so:
But the difference in the force on the top and bottom, DF, is the buoyant force. Let's call it FB.
Buoyant force equation
FBuoy is the buoyant force, r is the density of the fluid, g is the acceleration of gravity, and V is the volume of fluid that is displaced.
This is the exact same equation we worked out to find the weight of an object using density and volume. All we’re really doing is finding the weight of the fluid that was displaced.
Apparent Weight: If the object’s weight is less than the buoyant force, the object will float. If the object’s weight is greater than the buoyant force, the object will sink, but it will weigh less. We call this the apparent weight, FA. The apparent weight is simply the difference between its actual weight and the buoyant force.
Practice Problems:
- A cube of steel that measures 5.0 cm on each side is immersed in water. The density of steel is 9.0 x 103 kg/m3. The density of water is 1.0 x 103 kg/m3. What is the (a) buoyant force acting on the cube and what is (b) its apparent weight?
(a) Find the buoyant force.
The volume of the cube is: 
(b) Find the apparent weight.
The weight of the cube is: 
Now we can plug and chug:
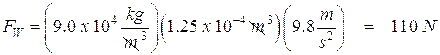
To find the apparent weight we use this equation:
- A cork has a volume of 4.25 cm3. The density of cork is 207 kg/m3. [a] What volume of the cork is beneath the surface when the cork floats in water? [b] What downward force is needed to completely submerge the cork?
[a]. The floating cork will displace a volume of water equal to its own weight. We can use the density of the cork to find its weight. With the weight, we can then calculate the volume of water displaced.
First let’s convert the volume of the cork to cubic meters:
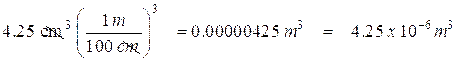
Now we find the weight of the cork:
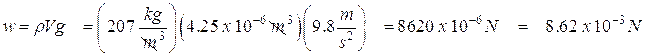
Now we can find the volume of water this represents. We set the buoyant force equal to this value:
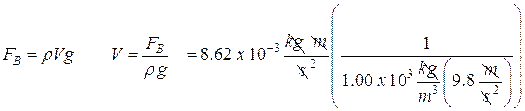
Or
(b) To find the force needed to sink the cork, we have to analyze the forces. First we will draw a FBD:
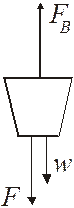
The forces are: FB the upward buoyant force, w the downward weight of the cork, and F is the force we must push down with to make it sink.
The sum of the forces must be zero:
We’ve already calculated the weight of the cork, w.
All we have to do is calculate the buoyant force, this is different than when the cork was floating because the entire cork is under water. So we use the cork’s entire volume to find FB.
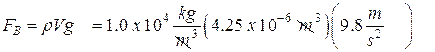
Now we can find the force
A large 9.0 m radius spherical balloon is filled with helium. The mass of the balloon bag and the little basket thingee that hangs underneath is 168 kg. How much additional weight can the balloon carry (assume it is at sea level)?
The fluid that is displaced is air, so we can easily find the buoyant force.
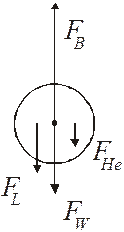
Let’s look at a FBD:
The sum of the forces must equal zero, this is the point where the upward force (the buoyant force) is equal to the total downward force – the weight of the bag, basket, and helium:
The forces are: FB (buoyant force), w (weight of bag and basket), FHe (weight of helium), and the lift (lifting force) FL ( weight that is to be lifted).
Volume of balloon: 
We already know w (weight of bag and basket). We can now calculate the buoyant force.
We’ll have to look up the density of the air and use that to find the buoyant force.
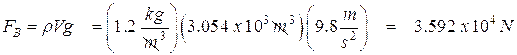
Next we have to find the weight of the helium. We have to look up its density as well.
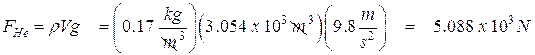
Now we can find the additional weight the balloon can lift.
The Famous Archimedes Story: Archimedes is quite a famous fellow. He is credited with many inventions. There is a wonderful story told about him that involves the idea of buoyancy and how he discovered his principal. Archimedes lived in Syracuse, a Greek city state in the third century BC. He was a natural philosopher and worked as a sort of technology troubleshooter for the king, King Hiero. It is said that Archimedes built some sort of lens that enabled him to set an invading fleet of ships on fire from the walls of the city. He also is supposed to have built some sort of lever device that could reach out over the walls of the city, grasp, pick up ships, shake them, and then drop them back into the water so they sank. Quite a deal. He also invented the Archimedes screw, a hollow tube that had a long screw inside it. One end could be placed in water, the screw would be rotated, and water could be pumped up the tube. The screw is still in use in the middle east.
So here goes the story. One day King Hiero asked Archimedes to determine if his new gold crown contained the actual quantity of gold given the crown maker. The king suspected that it might have been adulterated with some other less dear metal (like brass or silver). However, just in case the goldsmith had not cheated the king, the crown could not be harmed in any way (so no core samples).
Archimedes worried over the problem. He had to come up with a form of what today we call "nondestructive" testing. The king was not noted for being a patient man, so Archimedes was under a lot of pressure. Bad things could happen to people who failed to deliver for his majesty. Finally, unable to solve the problem, Archimedes decided to take a break and refresh himself with a nice bath. Well, the bathtub ended up being his salvation for it was in the tub that the solution finally came to him. As he dunked his body, he observed that the water level rose when he got in the tub. He also seemed to weigh less. The solution was at hand! He realized he could measure the volume of the crown by immersing it in water and could then determine if it was gold by finding its density. He, supposedly, was so excited that he leapt naked from the tub and ran through the streets of Syracuse shouting, "Eureka! Eureka! !" (I have found it).
The state motto of California is “Eureka”.
Source : http://teachers2.wcs.edu/high/bhs/mikek/AP%20Physics%20Course%20Notes/Fluids/2%20-%20buoyancy%20info.doc
Web site link: http://teachers2.wcs.edu
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Buoyancy formula definition factor notes
Buoyancy formula definition factor notes
Buoyancy definition
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does buoyancy mean ? Which is the meaning of buoyancy notes?
Buoyancy physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us