Circular motion
Circular motion
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Circular motion
We know that angles can be measured in degrees. They can also be measured in something called Radians*, where
Angle (in radians) =
Angular Velocity
Angular Velocity is the rate of change of angle with respect to time.
Angular Velocity is measured in radians per second, (rad/s).
The symbol for angular velocity is w (pronounced “omega”).
If an object is moving in a circle at constant speed, it is accelerating.
This is because while its speed is not changing, its velocity is. Why? Because velocity is defined as speed in a given direction, so if direction is changing, even though speed is not, then the velocity is changing, therefore the object is accelerating.
Relationship between Linear Speed (v) and Angular Velocity (w)
To derive v = r w
Remember we defined q (in radians) as s/r: 
Divide both sides by t: 
But w = q/t and v = s/t: 
Cross-multiply to get: 
Now try exercise 12.1, page 137 and 12.2, questions 1 – 5 page139.
Centripetal Force
The force - acting in towards the centre - required to keep an object moving in a circle is called Centripetal Force.
Centripetal Acceleration
If a body is moving in a circle the acceleration it has towards the centre is called Centripetal Acceleration.
Formulae for Centripetal Acceleration and Centripetal Force
a = rw2
but because v = rw we also have
F = mrw2
And because F = ma we get and also
Circular Satellite Orbits
Relationship between Periodic Time and Radius for a Satellite in Orbit*
Derivation of formula:
We compare two formulae which we have for Force:
- The first is the Universal Gravitational Force formula:
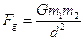
- The second is the Centripetal Force formula:
- Equate both forces (because both equations apply to satellite motion),
- Cancel one ‘m’ from both sides
- Replace the d2 in the first formula with r2 and cancel one ‘r’ both sides
- You now have
v2 Equation (1)
{You must be familiar with using this equation as it gets asked a lot}
- Now v = velocity = Distance/Time.
- Distance in this case is the circumference of a circle (2pR for circular satellite orbits)
- Þ
Þ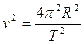 
Equation (2)
- Equating Equations (1) and (2) we get
Why so many f@#%ing formulae?*
Geostationary Satellites
These satellites are stationery over one position of the globe, and their orbit is called a Geostationary orbit.
We know that if we want a satellite to remain over a specific spot on the Earth’s surface it must have the same periodic time as the Earth (24 hours). The formula above allows us to calculate the height which the satellite must be at (approx 36,000 km above the equator.).
Leaving Cert Physics Syllabus: all higher level
Content |
Depth of Treatment |
Activities |
STS |
|
|
|
|
Circular Motion |
Centripetal force required to maintain uniform motion in a circle. |
Demonstration of circular motion.
Appropriate calculations. |
|
|
|
|
|
Gravity |
Circular satellite orbits – derivation of the relationship between the period, the mass of the central body and the radius of the orbit. |
Appropriate calculations. |
Satellites and communications |
Extra Credit
*Angles can also be measured in something called Radians
So why do we use radians? Well we’re used to dividing a circle up into 3600, but that’s completely arbitrary; it could be 1000, 2000 or just about anything else you want it to be.
It seems to go all the way back to the Mesopotamians over 6,000 years ago, who liked to work with the number 60, partly probably because it could be divided up so many different ways, i.e. 1, 2, 3, 4, 5, 6, 9, 12, 24 and 30. This got picked up by the Babylonians and passed on to the Egyptians. And from there to us. The circle has 6 × 60, or 360 parts. It’s popularity may also be related to fact that it is close to the number of days in the year.
Radians however are not arbitrary. If q is defined as arc length divided by radius, and we apply this to the number of radians in a full circle, we get arc length (which in this case is circumference of a circle - 2pr) divided by the radius r.
This gives us 2p radians. i.e. 360 (degrees) = 2p (radians).
You may have noticed on your calculator that the grad is another unit. Apparently some engineers use this unit. There are 400 grads in a circle. It has some advantages, but the sooner our school calculators lose this unit the better.
*Relationship between Periodic Time and Radius for a Satellite in Orbit
Congratulations
You have just arrived at an equation which bookmarks a seminal moment in the history of science.
Previous to this (16th century) a scientist called Johannes Kepler discovered empirically (i.e. by analyzing the motion of planets) that the square of the motion of these satellites is proportional to the cube of their radius.
Actually, if we’re going into detail here, he actually stole the necessary data from a colleague Tycho Brahe (some things never change).
The fact that Newton was able to demonstrate this relationship mathematically, by combining a well known equation for circular motion on Earth
with his own universal law of gravitation 
, had two very important consequences.
1. It proved Newton's Law of Gravitation was valid, which was very important in securing Newton's reputation as a giant of science.
2. Even more importantly, it demonstrated that 'the heavens' followed the same rules of science as those which operated here on Earth.
This meant that they were a legitimate area of study, and so Astronomy (which in turn led to Cosmology) was born.
* Why so many f@#%ing formulae?
Don’t know; I’m just glad it’s you and not me who has to know them.
For what it’s worth, none actually need to be learned off by heart;
w = q/t comes directly from the definition of angular velocity and q = s/r comes directly from the definition of a radian.
v = rw is obtained by dividing the previous equation by t on both sides (and this derivation needs to be known anyway).
The two formulae for acceleration are in the log tables; page 40 and the two formulae for force are obtained by simply multiplying the relevant acceleration by m.
The amount of formulae that need to be learned in Physics can be rather intimidating, so any help you can get to alleviate your suffering should be availed of. This chapter contains more formulae than most others, and possibly as a result of this students often try to avoid questions on circular motion when they can.
I suggest you get a sheet of A4 paper and put all these equations on it, showing how they are interconnected.
Taking a ‘big picture’ approach like this should help to reduce the intimidation factor.
Exam Questions
G = 6.7 × 10-11 N m2 kg-2, Radius of Earth = 6.4 × 106 m,
Mass of Earth = 6 × 1024 kg. Mass of the sun = 2 × 1030 kg. Mass of Saturn = 5.7 × 1026 kg.
Mean distance of Saturn from the Sun = 7.8 × 1011 m.
- [2006][ 2005]
Define angular velocity.
- [2006]
Derive the relationship between the velocity of a particle travelling in uniform circular motion and its angular velocity.
- [2002]
A particle travels at a constant speed of 10 m s-1 in a circle of radius 2 m. What is its angular velocity?
- [2006]
- A student swings a ball in a circle of radius 70 cm in the vertical plane as shown. The angular velocity of the ball is 10 rad s–1. What is the velocity of the ball?
- How long does the ball take to complete one revolution?
- [2005]
Define centripetal force.
- [2004]
Give an expression for centripetal force.
- [2004]
- Centripetal force is required to keep the earth moving around the sun.
What provides this centripetal force?
- In what direction does this centripetal force act?
- [2009]
A skateboarder of mass 70 kg maintains a speed of 10.5 m s–1 until he enters a circular ramp of radius 10 m.
What is the initial centripetal force acting on him?
- [2004]
The earth has a speed of 3.0 × 104 m s–1 as it orbits the sun.
The distance between the earth and the sun is 1.5 × 1011 m. Calculate the mass of the sun.
- [2009]
The moon orbits the earth. What is the relationship between the period of the moon and the radius of its orbit?
- [2008][2005]
Derive the relationship between the period of the ISS, the radius of its orbit and the mass of the earth.
- [2005]
- A satellite is in a circular orbit around the planet Saturn.
The period of the satellite is 380 hours. Calculate the radius of the satellite’s orbit around Saturn.
- [2008]
The international space station (ISS) moves in a circular orbit around the equator at a height of 400 km.
- Calculate the period of an orbit of the ISS.
- After an orbit, the ISS will be above a different point on the earth’s surface. Explain why.
- How many times does an astronaut on the ISS see the sun rise in a 24 hour period?
Exam Solutions
- Angular velocity is the rate of change of angle with respect to time.
- θ = s /r
Þ θ /t = s/rt
Þ ω = v /r
Þ v = ω r
- v = rw Þ w = v/r = 10/2 Þ w = 5 rad s-1
- v = ω r = (10)(0.70) = 7.0 m s-1
- T= 2πr/v = 2π(0.70)/v = 0.63 s
- The force - acting in towards the centre - required to keep an object moving in a circle is called Centripetal Force.
- Gravitational pull of the sun.
- Towards the centre.
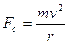= 70 (10.5)2/10 = 771.75 N
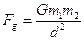and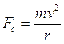 
Equating gives 
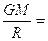v2 Þ Ms = v2R/G
Þ Ms = (3.0 × 104)2 (1.5 × 1011)/6.7 × 10–11 = 2.0 × 1030 kg.
Note
Strictly speaking the distance (or radius) is from centre to centre. In this case the question doesn’t specify whether the quoted distance is from surface to surface or from centre to centre, but it doesn’t really matter because the diameters of both spheres are insignificant relative to the overall distance. For an artificial satellite in orbit around a planet however the diameter of the planet would have to be taken into account.
- The period squared is proportional to the radius cubed.
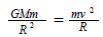See notes Circular Motion chapter for a more detailed derivation.
Þ
Þ
- T = 380 × 60 × 60 = 1.37 × 106 s
r3 = T2GM/4π2 Þ r3 = (1.37 × 106)2(6.7 × 10–11)( 5.7 × 1026)/ 4π2 Þ r = 1.2 × 109 m
- R = (400 × 103 + 6.4 x 106 ) = 6.8 × 106 m
Þ ÞT2 = 3.1347 × 107 ÞT = 5.6 × 103 s
- The ISS has a different period to that of the earth’s rotation (it is not in geostationary orbit).
- (24 ÷ 1.56 + 1) = 16 (sunrises).
Source : http://www.thephysicsteacher.ie/LC%20Physics/Student%20Notes/12.%20Circular%20Motion.doc
Web site link: http://www.thephysicsteacher.ie
Author : not indicated on the source document of the above text
Circular motion
Circular motion
Circular motion
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Circular motion mean ? Which is the meaning of Circular motion?
Circular motion physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us