Conservation of momentum
Conservation of momentum
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Conservation of momentum
AP Physics – Conservation of Momentum
We’ve studied the law of conservation of energy and found it to be a very powerful thing in the world of physics. Another very powerful conservation law has to do with momentum. This is the law of conservation of momentum.
Momentum is Conserved in an isolated system.
“Isolated system” means that there are no external forces acting on the thing.
The type of interaction that involves changes to momentum that we will deal with are called collisions. (Although not all of them are what we think of as a collision, as we shall see.)
The law of conservation of momentum means that for a collision in an isolated system, momentum must be conserved. This means that the total momentum of the system before the collision must be equal to the total momentum after the collision.
![]()
Here ![]() is the momentum before the event and
is the momentum before the event and ![]() is the momentum after the event.
is the momentum after the event.
Collisions can be very complicated. They can get so complicated that they can’t really be solved as a matter of fact. To simplify things, we will deal with collisions involving two bodies. We will also deal with one-dimensional collisions (like between balls rolling along a track), or else two dimensional collisions that occur at right angles.
This helps out a great deal. Imagine trying to deal with a violent collision between two cars. Before the collision you have two bodies in motion that have momentum. After the collision you’ve got thousands of them – all the bits and pieces of the cars flying off in every imaginable direction.
Collisions can be classified according to the energy interaction that takes place:
Elastic collision º kinetic energy is conserved
Inelastic collision º kinetic energy is not conserved
Perfectly inelastic collision º objects stick together and have the same velocity.
Application of Conservation of Momentum: On the AP Test, you will only be given the equation for momentum, p = mv. From this you will have to derive the formula for a two-body collision. Here’s how to do it.
We begin with a two-body collision where each object has some velocity prior to the collision. Both objects have momentum equal to the mass times the velocity.
The total momentum before the collision is:
![]()
After the collision the velocities will have changed. The total momentum will be:
![]()
We know that the momentum before must equal the momentum after:
![]() so
so ![]()
So here is an equation which will work for any two-body collision:
![]()
Perfectly Inelastic Collisions: These are collisions where the two objects stick together after they collide.
The key thing to remember here is that after the collision both objects stick together and have the same velocity.
- We see a 15 000 kg railroad car moving along the track at 2.5 m/s. It collides and couples with a stationary 12 500 kg car. What is the new velocity of the two cars?
![]()
![]()
The velocity of each is the same (they’ve joined together into a “single body”) so we can simplify the equation for the final momentum:
![]() Now we set the two equations equal to each other:
Now we set the two equations equal to each other:
![]()
And we get our equation. Now we solve for the final velocity:
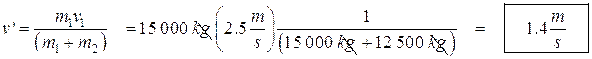
- 2 mud balls collide in a perfectly elastic collision. One has a mass of 4.0 kg, the second has a mass of 3.5 kg. The first one has an initial velocity of 3.4 m/s, the second has an initial velocity of – 4.8 m/s. What is their velocity after the collision?
![]()
![]()
![]()
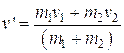
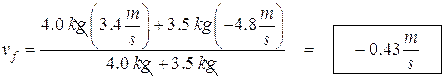
The negative sign means that they are going in the opposite direction from what our first mud ball was doing. We chose its direction as the positive direction.
Bouncing Collisions: When two objects collide and bounce off each other, there are two possible energy interactions. Kinetic energy can be conserved or not conserved. If it is conserved, then we have a perfectly elastic collision. The other possibility is that some of the kinetic energy is transformed into other forms of energy. This is mostly what happens in the real world.
The type of problem you will be tasked with solving will have two objects bouncing off each other. You will know three of the four velocities and solve for the fourth. You may be asked whether kinetic energy is conserved and, if it isn’t, how much kinetic energy is lost.
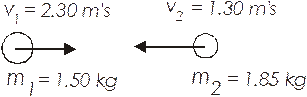
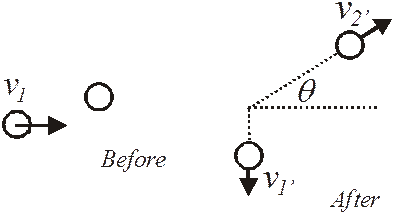
Two balls hit head on as shown, what is the final velocity of the second ball if the firstone’s final velocity is –1.50 m/s?
The general conservation of momentum equation is:
![]()
All we have to do is solve for v2’. 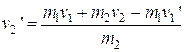
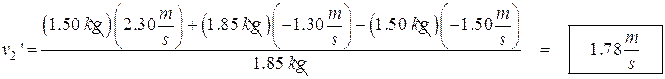
- Two balls roll towards each other and collide as shown. The second’s ball velocity after the collision is 3.15 m/s. (a) What is the velocity of the first ball after the collision? (b) How much kinetic energy is lost during the collision?
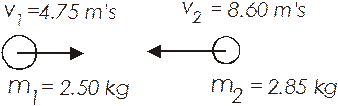
(a) ![]()
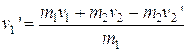
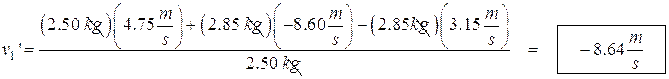
(b) Difference in kinetic energy before and after collision:
Kinetic energy before the collision: ![]()
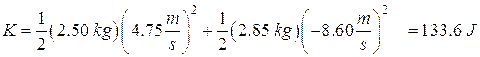
Kinetic energy after the collision ![]()
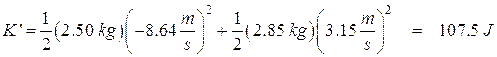
![]()
What happened to this energy? Where did it go? Well, it was converted into some other form of energy, most likely heat.
Explosions: The final type of collision is the explosion. Not like you get with a bomb. That would be one very hard problem. No, we want us a nice, simple two body explosion. An example you ask? Okay, you stand on a skateboard and throw a bowling ball away from you. This would be a simple two-body explosion.
The idea of an explosion is that you have two bodies that are at rest – this means that they have no momentum, don’t it? Anyway, the explosion takes place and the bodies end up moving away from each other. Because momentum is conserved, their final momentum, when added together, must still equals zero; the momentum they started out with.
- A 23 kg girl is standing on a low friction 2.0 kg cart. She is at rest. She then throws a heavy 8.9 kg rock, giving it a speed of 7.5 m/s. What is the final speed of the girl/cart system?
![]() becomes:
becomes: ![]()
Solve for the speed of the girl: 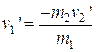
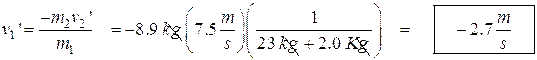
The negative sign means that the girl is going in the opposite direction from the rock.
AP Test Question: Two identical objects A and B of mass M move on a one-dimensional, horizontal air track. Object B initially moves to the right with speed vo. Object A initially moves to the right with speed 3vo, so that it collides with object B. Friction is negligible. Express your answers to the following in terms of M and vo.
a. Determine the total momentum of the system of the two objects.
![]()
- A student predicts that the collision will be totally inelastic (the objects stick together on collision). Assuming this is true, determine the following for the two objects immediately after the collision.
i. The speed ii. The direction of motion (left or right)
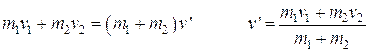
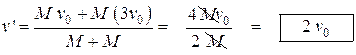
Moves right (positive direction).
When the experiment is performed, the student is surprised to observe that the objects separate after the collision and that object B subsequently moves to the right with a speed 2.5 vo .
- Determine the following for object A immediately after the collision.
i. The speed ii. The direction of motion (left or right)
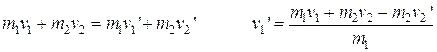
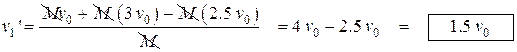
Object A move to the right
d. Determine the kinetic energy dissipated in the actual experiment.
![]()
![]()
![]()
![]()
![]()
Glancing collisions: This type of collision takes place in two dimensions. Collisions on a pool table are good examples of this type of collision. Momentum still has to be conserved – it’s the law for crying out loud! But the problems can become fairly complex. One technique to keep track of what’s going on is to break things into x and y components:
![]()
![]()

We will deal with greatly simplified collisions. Basically with right angles and one of the bodies at rest at the beginning.
- An 8.00 kg mass moving east at 15.0 m/s strikes a 10.0 kg mass that is at rest. The 8.00 kg mass ends up going south at 4.00 m/s. (a) What is the velocity of the second ball?
(a) We analyze the momentum in the x and y directions.
The x direction:
![]()
This is because the second body has no initial velocity so it has no initial momentum in either the x or y direction. After the collision, the first body has momentum only in the y direction, so the x direction momentum after the collision involves only the second body.
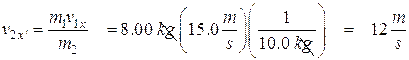
Now let’s look at the y direction:
![]()
The first body’s initial motion is only in the x direction, therefore it has no initial momentum in the y direction. The second body is at rest at the beginning so the total initial y direction momentum is zero.
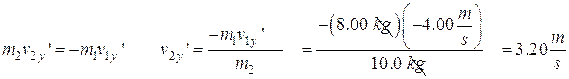
Now we can solve for the velocity of the second body using the Pythagorean theorem.
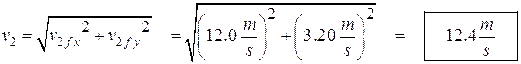
Now we find the angle q:
Trigonometry is just the thing to find the old angle:
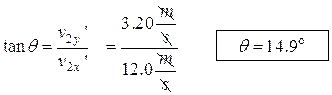

A 2.0 kg block is sliding on a smooth table top. It has a totally inelastic collision with a 3.0 kg block that is at rest. Both blocks, now moving, hit the spring and compress it. Once the blocks come to rest, the spring restores itself and launches the blocks. They slide off the right side of the table. The spring constant is 775 N/m. Find: (a) the velocity of the two blocks after the collision. (b) The distance the spring is compressed. (c) The velocity of the blocks after they leave the spring. (d) The distance the blocks travel before they hit the deck after the leave the tabletop. (e) The kinetic energy of the blocks just before they hit the deck.
(a) ![]()
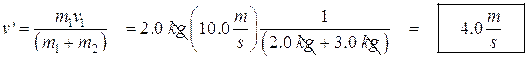
(b) 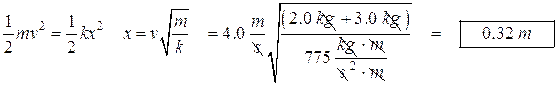
- If energy is conserved in the spring, they should have the same speed when they leave as they had going into the spring. So they should be moving at 4.0 m/s to the right.
(d) Find the time to fall:
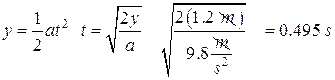
![]()
(e) The kinetic energy of the blocks at the bottom (just before they hit) must equal the potential energy at the top of table plus the kinetic energy the blocks had before they began to fall.
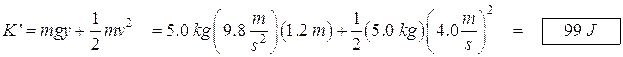
Examples of Conservation of Momentum:
When you fire a rifle, you experience the consequences of the conservation of momentum. The bullet is fired out of the thing at a very high velocity. Because momentum must be conserved, the rifle must end up going in the opposite direction. We call this backwards motion the “recoil”.
Rockets, which we discussed using Newton’s third law, can also be explained using the conservation of momentum. The rocket is an explosion type event. It contains a large amount of fuel. The fuel is ignited and blasts out of the rocket nozzle at a high velocity. The rocket must accelerate in the opposite direction so that momentum can be conserved.
Source : http://teachers2.wcs.edu/high/bhs/mikek/AP%20Physics%20Course%20Notes/Momentum/2%20-%20Conservation%20of%20Momentum.doc
Web site link: http://teachers2.wcs.edu
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Conservation of momentum
Conservation of momentum
Conservation of momentum
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Conservation of momentum mean ? Which is the meaning of Conservation of momentum?
Conservation of momentum physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us