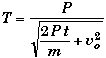Physics definition of work in physics
Physics definition of work in physics
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Physics definition of work in physics
Definition of Work in Physics
- When a force acts to move an object, we say that Work was done on the object by the Force.
Work done by a Constant Force:

![]()
= Force vector applied to the object/system. |
|
Fs |
= Component of Force along the direction of movement. |
|
= Displacement vector. |
s |
= Distance the system is displaced. |
f |
= Angle between the displacement and the force. |
|
= Scalar or Dot product of the force vector and the distance vector |
- Work is usually defined in terms of the dot product because it is only the component of the force along the direction of motionof the object - F cos(q) - which does any work and the dot product nicely expresses product in a compact form. One corollary is that the perpendicular component of the force can never do any work on object.
- Work is the measure of a quantity that is capable of accomplishing Macroscopic Motion of a System due to the action of a Force over a Distance.
- Force is the agent of change, and Work is a measure of the change.
- The Force does the Work, not the agent that created the Force. Do not confuse the work you do to create a force with the work done by the force you create; they are not the same. The force you exert holding a 100 pound barbell above your head does no work on the barbell while the barbell is at rest, but you do work (on a molecular level) to create that force.
- Work is related to the distance a force moves an object and not the time it takes to move the object.
- A Force does no work unless the system is free to move "along the direction" of the Force applied. When a Force and the object's displacement are perpendicular, the work done by the force is zero.
Work Done By a Variable Force
If the force is not constant along the path of the object we need to calculate the over very tiny intervals and then add them up. This is exactly what the integration over differential small intervals of link can accomplish.
![]()
= Force vector function that is applied to the body. |
|
Fs(s) |
=Component of force function along the direction of movement. |
F(s) |
= Function of the Magnitue of the force vector along the displacement curve. |
|
= Dot or Scalar product of the force vector and the differential displacement vector |
d |
= Differential displacement vector. |
ds |
= Differential displaced. |
f |
= Angle between displacement and the force. |
so |
= Initial location of the body |
sf |
= Final location of the body |
When the force is constant this definition of Work becomes identical to that above for the work done by a constant force.
In order to calculate the work done by a variable force, one needs to know how the force changes over the path of the object's motion.
Example: Work done by Spring
The force that a spring exerts on an object attached to its end not constant as the spring is stretched and is given by F(s) = -k s (see Hook's Law). To calculate the work done by the spring when it is stretched from xo to xf we integrate F(s) over ds.
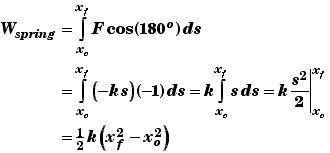
The angle between F and ds is 180o since the force is in the opposite direction of the motion of the end of the spring when the spring is being stretched.
Two Examples of Work |
Force |
External Work Needed |
Work done by the Force |
Gravity |
Fgrav = –mg |
Wext = mg(h2 - h1) |
Wgrav = –mg(h2 - h1) |
Spring |
Fspring = –kx |
Wext = 1/2 k (x22 - x12) |
Wspring = –1/2 k (x22 - x12 |
Work, Force, and Energy
![]()
* Work is the measure of a quantity that is capable of accomplishing Macroscopic Motion of a System due to the action of a Force over a Distance.
* Force is the agent of change, and Work is a measure of the change.
* The Force does the Work, not the agent that created the Force. Do not confuse the work you do to create a force with the work done by the force you create; they are not the same. The force you exert holding a 100 pound barbell above your head does no work on the barbell while the barbell is at rest, but you do work (on a molecular level) to create that force.
* Work is related to the distance a force moves an object and not the time it takes to move the object.
* A Force does no work unless the system is free to move "along the direction" of the Force applied. When a Force and the object's displacement are perpendicular, the work done by the force is zero.
* The Energy transferred into a system by the action of a Force is the Work done on the System.
* If system A does work then energy flows out of the system A. If another system does work on system A then energy flows into the system A from the other system.
* There is no such thing as pure energy. Energy is a property of a system which depends upon the system's mass and speed, and sometimes on its position.
* Mass and Energy have much in common. Einstein's famous equation E = mc2 shows that mass is itself a form of "stored" energy.
* Energy is a scalar quantity. Like mass, it has no direction associated with its magnitude.
Energy Flow when doing Work
System A Does Work on System B
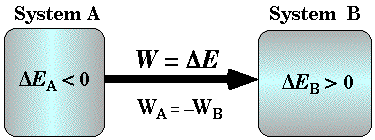
When a SYSTEM does WORK it loses energy: DESYS < 0
When WORK is done ON a SYSTEM it gains energy: DESYS > 0
- Whenever work is done, energy flows from one system to another. What one system loses the other system gains - the conservation of energy.
- Work is a transfer of energy when one system exerts a force on another system. It is not a property of a system like a system's mass, volume, or temperature.
Work-Energy Theorem:
- The energy associated with the work done by the net force does not disappear after the net force is removed (or becomes zero), it is transformed into the Kinetic Energy of the body. We call this the Work-Energy Theorem.
![]()
- If the body's speed increases, then the work done on the body is positive and we say its Kinetic Energy has increased. Whereas if the body's speed decreases then it kinetic energy decreases and the change in kinetic energy DKE is negative. In this case the body does positive work on the system slowing it down or alternately the work done on the body is negative.
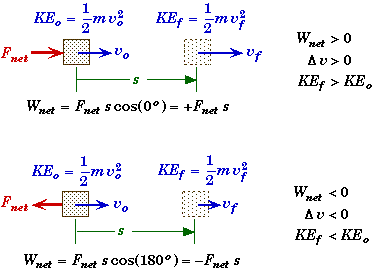
- If the object is not rigid and any of the forces acting on it deforms the object, then the Work-Energy Theorem will no longer be valid. Some of the energy transferred to the object has gone into deforming the object and is no longer available to increase or decrease the object's Kinetic Energy.
Derivation of Work-Energy Theorem using a Constant Net Force
Frame of Reference:
Direction of the Net Force.

Start with Newton 2nd Law for one-dimensional motion:
![]()
Next use the Equations for Constant Acceleration that does not involve time:
![]()
Calculate the Net Work using the above relationships:
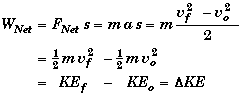
Many problems you encounter related to Work and Energy will have constant forces. While you are trying to learn how to use the concepts of Work and Energy, avoid using Newton's Second Law to solve these problems or else you will have missed the opportunity to learn how to use Work and Energy to solve them. It is reasonable to use the Second Law approach as a way to double-check your Work-Energy solutions.
Derivation of Work-Energy Theorem using a Variable Net Force
Frame of Reference:
Direction of the Net Force.

To reduce the complexity of the derivation, we will assume that the direction of the Net Force is constant while the work is being done. The Work-Energy Theorem is still valid if the net force changes direction as well as magnitude while the work is being done, provided the body is rigid.
The key step is to convert the calculus definition for acceleration into an expression that is a derivative of x.
![]()
Plug this and the Second Law into the definition for Work, and integrate.

Here we have used the relation ![]() with x = v to do the integration. Also observe that we have assumed that the body's mass does not change while the force is being applied so that we can remove it from under the integral.
with x = v to do the integration. Also observe that we have assumed that the body's mass does not change while the force is being applied so that we can remove it from under the integral.
Work Energy Problem-Solving
Finding the Work - Summery:
1. Choose a system on which to calculate the work.
2. Determine all the forces acting on the system.
3. Ascertain the displacement of the system.
4. Calculate the work done by each force or the net force.
What object or group of objects shall I focus on as a system ?
* It is important to have a clear idea of the system on which you are going to calculate the work, since work always involves a transfer of energy between two different systems. One system loses some energy, and the other one gains that energy.
What does the free-body force diagram look like for this system ?
* This part of the problem-solving process is the same as you used to solve dynamics problems involving Newton's Second Law.
What are the initial and final locations of the system ?
* Since non-zero work always involves movement, the system will have an initial and a final location. For problems involving kinetic energy, you will need to calculate (or find) the initial and final kinetic energies of the system.
![]()
* Identifying these two locations is useful in determining the displacement path of the system, since the path of the system is also the integration path for variables force,
![]()
What is the angle between each of the forces and the system's displacement ?
* Some forces may be perpendicular to the system's displacement and thus do no work. Only the component of a force that is parallel to the displacement will do any work.
* Resolve the forces into components that are parallel Fs and perpendicular to the system's movement.
![]()
Alternately you can also find the angle between a force and the system's displacement to calculate the work from
![]()
If F is constant.
![]()
What is the sign of the work done by each of the forces ? Is this reasonable ?
* If a force -- acting by itself -- will cause the system to speed up, then the force must do positive work. If a force -- acting by itself -- would cause the system to slow down or reverse direction, then its contribution to the net work must be negative.
* When the component of a force is in the same direction as the object's initial motion, then its work contribution will be positive. A force's contribution will be negative if it has a component of force that is opposite to the system's initial motion.
Is the force constant over the system's motion-path ?
* When the force is constant, the work done by that force is simply the component of the force along the path times the path-length, W = Fs s. Otherwise, you will have to determine the force's functional dependence along the path, F(s), so that you can integrate the force-distance integral,
![]()
How can I apply the Work-Energy Theorem to analyze the problem ?
* Express the initial and final kinetic energies of the system in terms of the quantities given and the unknowns requested.
* Apply the Work-Energy Relationship, Wnet = KEf - KEo . Look at the resulting expression to see if you can solve for any unknowns.
Pushing a Puck on the Parquet
A 350 gram puck sitting on a wood parquet floor is pushed by a long stick that makes an angle of 22.0o with the surface. The stick is propelled by a person who exerts a constant force of 19.0 N directed along the stick. The person stops pushing after the puck moves 50.0 cm, giving the puck a velocity v. The coefficient of kinetic friction between the floor and the puck is .440. |
|
Analyze the flow of energy into and out of the puck by calculating the work done by each of the following: the applied force, the force of gravity, the force of friction, the normal force, and the net force acting on the puck. |
|
Calculate the velocity of the puck when the person stops pushing with the stick. |
|
Sketch and Process:
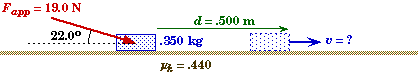
An object is propelled across a rough horizontal surface by a constant force that makes some angle with its direction of motion. The object's motion is retarded by friction.
Reference Frame:
The origin will be the initial location of the puck. We pick the direction of the net force to be the positive direction.
The clock starts when the force is applied.
Givens and Labels:
Fapp |
= 19.0 N |
(Force applied along the stick) |
q |
= 22.0o |
(Angle of the applied force) |
m |
= .350 kg |
(Mass of the puck) |
d |
= .500 m |
(Horizontal distance over which the force is applied) |
mk |
= .440 |
(Coefficient of kinetic friction) |
v |
= ? |
(Final velocity of the puck) |
Wapp |
= ? |
(Work done by the applied force) |
Wf |
= ? |
(Work done by the force of friction) |
Wg |
= ? |
(Work done by the force of gravity) |
Wn |
= ? |
(Work done by the normal force) |
Wnet |
= ? |
(Work done by the net force) |
Relevant Physics:
For part A the work is done by a constant force so that
![]()
where f is the angle between the force and the direction of motion.
For part B the work-energy theorem can be applied to find the puck's final kinetic energy.
![]()
Knowing the final kinetic energy, we can find the puck's final velocity.
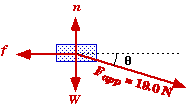 To calculate the work done by the various forces, we need to draw a free-body force diagram to determine what forces are acting on the puck and the direction of those forces relative to the puck's movement. We will also need to calculate the x and y components of these forces - the force of gravity, the normal force, the force of friction, the applied force, and the net force.
To calculate the work done by the various forces, we need to draw a free-body force diagram to determine what forces are acting on the puck and the direction of those forces relative to the puck's movement. We will also need to calculate the x and y components of these forces - the force of gravity, the normal force, the force of friction, the applied force, and the net force.
Force of Gravity:
![]() Note that here "W" stands for Weight, which is a Force, and not Work. The context in which they are used distinguishes their meaning.
Note that here "W" stands for Weight, which is a Force, and not Work. The context in which they are used distinguishes their meaning.
Applied Force:
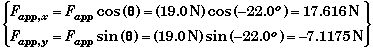
Normal Force:
Since the vertical component of the applied force will increase the force pressing the puck into the parquet floor, the normal force will be greater than just the weight of the puck.

Force of Friction:
![]()
Net Force:
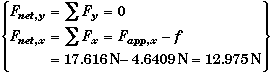
(A) Find the work done by each of the forces acting on the puck.
The magnitude of the components of the force were found in the Relevant Physics discussion.
Applied Force Work:
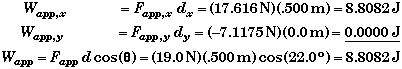
Gravitational Force Work:
![]()
Normal Force Work:
![]()
Frictional Force Work:
![]()
Total and Net Work:
![]()
Summary of the Energy Flow
Work done by Gravity |
|
= |
0 J |
Work done by Normal Force |
|
= |
0 J |
Work done by Applied Force |
|
= |
8.81 J |
Work done by Friction |
|
= |
-2.32 J |
Total Work done by all forces |
|
= |
6.49 J |
Work Done by the Net Force |
|
= |
6.49 J |
Discussion:
Normally I do not bother to explicitly include the cosine function when a force is parallel or perpendicular to an object's displacement. In fact, I do not bother with any forces that are perpendicular, since those forces do no work. Moreover, it is more physically meaningful to keep track of the sign of the work done by a particular force from its action on the object. In this case I know that the frictional force will take energy out of the moving object and thus should be negative, whereas the applied force is adding energy to the moving object and thus should be positive.
Also, observe that the net work could be found in different ways. You could find the net force first and then calculate the net work directly from it, or you could find the work done by each force and then add them up. The later is more time consuming, but it does allow you to examine the value of each force's contribution to the work to see if each one looks reasonable.
(B) Find the velocity of the puck when the person stops pushing with the stick.
The work energy theorem gives,
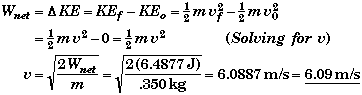
Energy Flow

Non-Hookian Spring
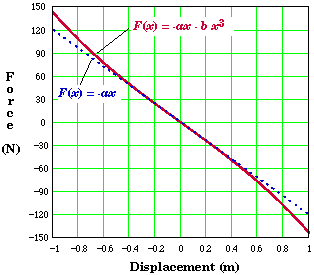
A non-Hooke's-Law spring has a restoring force that depends on its displacement from equilibrium according to the equation F(s) = -as - bs3. The constants a and b are given as a = 120 N/m and b = 23.0 N/m3. The length of the unstretched spring is 2.00 m. |
|
(A) |
Determine the symbolic equation for the amount of work it would take to stretch or compress the spring's length by an amount x relative to it unstretched length. |
(B) |
How much work does it take to compress the spring 56.0 cm ? |
If 34.0 joules of energy are used to stretch the spring, what would be the length of the spring ? |
|
Sketch and Process:
A spring is stretched or compressed by a force applied to one end. The spring's restoring force has two terms.
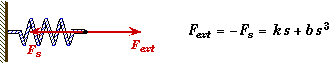
Reference Frame:
It is implied that the location of the origin is located at moveable end of the spring when it is unstretched. The equation of the spring-force varies with respect to this spacial location, and so the equation would have a different form if you located the origin any other place. If you place the origin at the end of the spring attached to the wall and the length of the unstretched spring was L, then the equation would take the form,
![]()
There is no time involved. The work is independent of how fast or slow the spring is stretched or compressed.
Givens and Labels:
F(s) |
= -as - bs3 |
(Spring force's dependence upon displacement.) |
s |
= ? |
(Displacement from equilibrium variable) |
a |
= 120 N/m |
(One spring constant.) |
b |
= 23.0 N/m3 |
(Second spring constant) |
L |
= 2.00 m |
(Length of the unstretched spring) |
Wext |
= ? |
(Work done by external force.) |
Relevant Physics:
This spring is basically a Hooke's-law spring, F(s) = -k s, with a second order term, -b s3. Such an equation represents a higher order approximation to the behavior of a real spring. For small displacements the second order term is small and the spring behaves like a Hookian spring. It is only when the displacement is large that the second term become significant.
The negative signs are needed so that the spring's force is a restoring force, i.e., the force is opposite the displacement.
From Newton's Third Law the force applied by an external agent will be the negative of the force exerted by the spring.
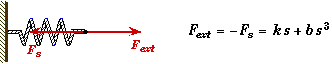
The work done by an external agent will always be positive to compress or stretch the spring from equilibrium. This always has to be true for a spring and it is why the spring force has to be to an odd power of its displacement.
If you calculated the work done by the spring when it is compressed or stretched you find that it would be a negative number. Because the force is a conservative force this means that spring stores the energy.
Note that it is also assumed that the force applied by the external agent changes in such a way that it exactly matches the force exerted by the spring at each point. Alternately you could say that the work we find will be the minimum work it take to stretch or compress the spring.
The work done by a variable force can be found by integrating the force over it displacement.
![]()
(A) Find the work done by an external agent to stretch the spring a distance x.
The work is done by a variable external force. Recall that Wext = -Wspring.
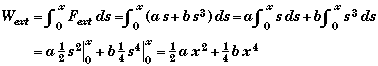
We have use the relation ![]() to do the integration.
to do the integration.
The first term is just the work needed for a Hooken spring.
Since the spring force is assumed to be a conservative force the answer we found also represents the potential energy for this type of spring.
(B) Find Wext when x= .56 m.
Using the work-function expression we found in part A.
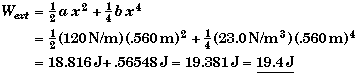
We could check to see if our answer is in the right ballpark by using what we know about Hookes-Law spring. - namely that it is linear function of displacement.
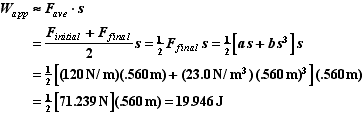
For a Hooken spring this approximation would be exact since Hooke's force is a linear function of the displacement. It is still pretty close - mostly because the spring is not compressed very far.
(C) Find x when Wext = 34.0 J.
Solve the work equation found in part A for x when the work equals 34.0 J.
![]()
Analytical Solution:
Let z = x2 so the above equation becomes a quadratic equation in z,
![]()
Using the solution of a quadratic equation we get,
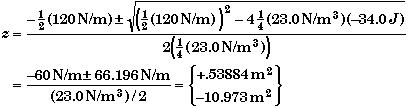
We discarded the negative solution since the square root of a negative number would be an imaginary number. Taking the square root of z gives x,
![]()
Since the spring is stretched, x is positive and the length of the spring is
![]()
Symbolic Solution:
Following the same procedure above but leaving in the symbols rather than using numbers one would obtain after a little tiding up to make the solution look simple,
![]()
Calculator Solve Mode:
This is an ideal equation to use your calculator's solve mode since the only unknown variable is x. The above equation has four possible solutions so you will need to decide which one is the correct answer. It would be the one that is both real and positive.
Graphical Solution:
Another method would be plot the work as function of x and look for the value of x that produces 34.0 J.
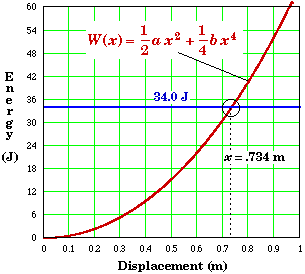
Power:
* The rate at which work is being done on/by a system.
* The rate of energy transfer into or out of a system.
Definition:
Average Power![]()
Instantaneous Power ![]()
Units:
SI W = watt = J/s = Joules per second
Other Units:
kW = kilowatt = 1000 W
hp = horsepower = 746 W
Scalar Product Power-Velocity Relationship: ![]()
Typical Values of Power
Person Resting |
75 W |
Sustained Human output |
300 W |
1 horsepower |
746 W |
Automobile (30 mph) |
105 W |
Locomotive |
106 W |
Aircraft Carrier |
108 W |
Jet Airliner |
108 W |
Grand Coulee Dam |
1010 W |
Tidal Friction Loss |
1012 W |
US Power Consumption |
1013 W |
Solar Output |
1026 W |
Quasar |
1040 W |
Air Drag on a Bicyclist
The main source of resistance for a bicyclist is air resistance. Air resistance can be modeled by where CD is the drag coefficient, A is the cross-sectional area perpendicular to the air flow, r =1.29 kg/m3 is the density of air, and v is the velocity of the bicyclist relative to the air. Assume that the cyclist has a cross-sectional area of .750 m2 and a drag coefficient of 1.40. |
|
(A) |
Calculate the drag force on the cyclist when moving at a constant speed of 40.0 km/hr. Also determine the power the cyclist inputs into the bicycle to maintain a constant speed of 40.0 km/hr. |
(B) |
Show that the power required to maintain a constant speed is proportional to v3. |
(C) |
Estimate the work delivered to the bicycle (by the cyclist) during a 5.00 km leg on level ground at a constant speed of 40.0 km/hr with no head or tail wind. |
If the drag coefficient is reduced by half, how much faster would the cyclist go using the same power output as part B ? |
|
Sketch and Process:

A moving cyclist is slowed by air drag. The cyclist produces enough power to move at a constant speed.
Reference Frame:
The system consists of both the bicyclist and the bicycle. Note that the power is supplied by the cyclist to both parts of the system.
We only need to specify an origin for part C, which will be at the start of the 5.00 km leg.
Givens and Labels:
Papp |
= ? |
(Power applied by Cyclist) |
Fdrag |
= .5 CD Ar v2 |
(Drag force on System) |
CD |
= 1.40 |
(Drag coefficient) |
A |
= .750 m2 |
(Cross-sectional area of System) |
r |
= 1.29 kg/m3 |
(Density of air) |
v |
= 40.0 km/hr |
(Velocity of System) |
d |
= 5.00 km |
(Distance traveled) |
Relevant Physics:
Since the speed is constant, Newton's 1st Law implies that the net force on the system must be zero. Newton's 2nd Law implies that the force producing the motion must be equal to the drag force.
![]()
Because of this, we do not need to be concerned with the complicated way the cyclist actually produces a force that propels the system along.
Since the instantaneous power is equal to force times velocity, we can find the cyclist's power input into the system of cyclist and bicycle.
Papp = Fapp v = Fdrag v
(A) Find the drag force and power requirement at 40.0 km/hr.
Using the equation given for the drag force,
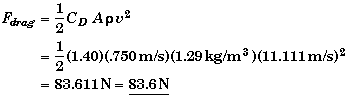
The power the cyclist inputs,
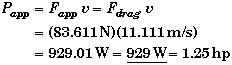
(B) Find Papp as a function of the speed.
This is the analytical solution for the power in part A.
![]()
This shows that doubling the speed requires 8 times the power output, since the power requirement is proportional to the velocity cubed, 23 = 8.
Not surprisingly, the maximum theoretical power that a wind driven power-generator can produce is also proportional to the third power of the wind-velocity.
If there is a head wind or a tail wind, then v will change, causing the power needed to increase or decrease as the third power of the speed of the cyclist relative to the air.
Bicyclists often ride close behind each other - slip streaming - because this reduces the effective velocity of the air stream that the trailing cyclist encounters. The trailing cyclist takes advantage of the back-eddies of air roiling behind the lead cyclist.
(C) Find Wapp for d = 5.00 km.
Since the speed is constant we can determine the time it takes for the cyclist to travel 5.00 km from the kinematic equation for constant speed.
![]()
From the definition of power and the fact that power is constant
![]()
Then
![]()
(D) Find v when CD is halved and power is same as part A.
Solve for v in the power equation in part B, and plug in the new value for CD
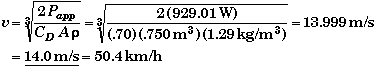
Most bicycle riders bend over because it reduces the cross-sectional area presented to the wind, as well as changing the drag coefficient slightly.
The fastest speed records for bicycles are held by bicycles that are enclosed in a kind of streamlined shell. As of 1993 this was approximately 70 mi/hr or around 30 m/s.
Constant Power Bat-Engine
Suppose Batman developed a jet-engine that was capable of delivering a constant power output of 500 kW to the Batmobile. The engine is designed to "kick in" when the acceleration of the Batmobile will be 5g's or less. Assuming no frictional loses, that the road is horizontal, and that the fully occupied Batmobile has a mass of 1100 kg: |
|
(A) |
At what minimum speed can the engine be engaged ? |
(B) |
If the engine is engaged when the Batmobile is moving at 40.0 km/h, how fast will the Batmobile be traveling after .360 seconds ? |
(C) |
If the engine is engaged when the Batmobile is moving at 40.0 km/h, determine the distance the Batmobile will travel in .360 seconds. |
(D) |
Show that the thrust produced by the engine on the Batmobile is not constant, but decreases with time according to |
Sketch and Process:
![]()
A jet-engine on the Batmobile produces constant power output, there by accelerating the Batmobile. Consider the situation when there are no drag forces.
Reference Frame:
Position of the Batmobile when the jet-engine is engaged. The clock also starts when Batman puts the petal to the metal.
Givens and Labels:
P |
= 500 kW |
(Power delivered to the Batmobile) |
m |
= 1100 kg |
(Mass of the Batmobile) |
t |
= .360 s |
(Duration of constant power output) |
vo |
= ? |
(Velocity of the Batmobile when engine is engaged) |
vf |
= ? |
(Velocity after 10 seconds) |
ao |
= 5g |
(Initial acceleration in part A) |
T(t) |
= ? |
(Force acting on the car as a function of time) |
Relevant Physics:
The definition of power P = dW/dt and P = F v both apply to this problem. Since there are no frictional losses and the road is flat, the work done by the engine is the net work done on the Batmobile. Using the work-energy theorem
![]()
Since the power is constant we can integrate it to find the net work,
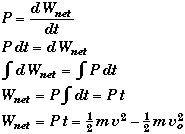
Thus,
![]()
(A) Find vo such that ao = 5g.
Using Newton's Second Law and the power-velocity relationship we can solve for the velocity.
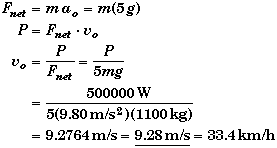
(B) Find v when t = .360 s and vo = 40 km/h = 11.111 m/s.
Since the power is constant, the net work is equal to the power times the time.
![]()
By the work-energy theorem the net work is also equal to the change in the Batmobile kinetic energy. We can solve this relationship for the final velocity.
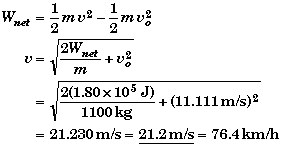
(C) Find x when t = .360 s.
One could be tempted to determine the distance from
![]()
However, this is only valid if the Batmobile has a constant acceleration, which it doesn't. Therefore we will need to use calculus to determine the distance traveled. From part B
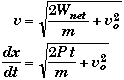
Multiplying by dt and integrating both sides,
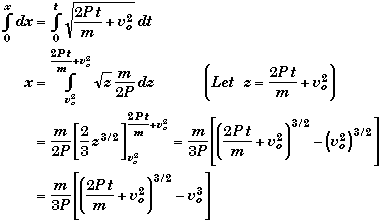
At .360 of second,
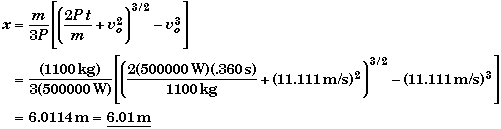
(D) Find expression for the thrust-force T(t).
First of all the thrust of the jet-engine is just the net force on the Batmobile assuming the normal engine shuts off. There are two ways we could find the force.
First and easiest, uses P = T v and the results of part B,
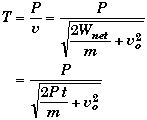
Second is to use Newton's 2nd law and the results we found in part B,
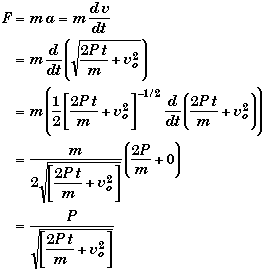
The force produced by the engine decreases with time as the Batmobile speed increases. This is not a very good design. It would be better to design a constant trust engine rather than constant power. Not surprisingly, the power output of a constant force-engine will have to increase with time.
If the engine is started at 40.0 km/h then the initial thrust is given by,
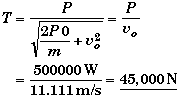
Some Important Units of Energy
MECHANICAL ENERGY:
Metric Units: |
SI: Joule (J) |
1 J = 1 N-m |
English Units: |
foot-pound (ft-lbs) |
1 ft-lbs = 1.356 J |
HEAT ENERGY:
Calorie (Cal) |
1 Cal = 4.186 J |
British Thermal Unit (BTU) |
1 BTU = 1,055 J |
ELECTRICAL & ATOMIC ENERGY:
Electron Volt (eV) |
1 eV = 1.6x10-19 J |
Kilowatt-hour (kWh) |
1 kWh = 3.6x10+6 J |
Source: http://physics.mtsac.edu/4A/4A%20Text/Work.doc
Web site link: http://physics.mtsac.edu/
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Physics definition of work in physics
Physics definition of work in physics
Physics definition of work in physics
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Physics definition of work in physics mean ? Which is the meaning of Physics definition of work in physics?
Physics definition of work in physics physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us