Density and pressure
Density and pressure
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Density and pressure
Density is defined as Mass per unit Volume
The unit of density is the kgm-3
The symbol for density is r (pronounced ‘row’ – same symbol as for momentum – don’t ask!)
Pressure is defined as Force per unit Area.
The unit of Pressure is the Pascal (Pa)
Pressure in a liquid at a height h below the surface
P = rgh
Archimedes’ Principle states that when an object is immersed in a fluid, the upthrust it experiences is equal to the weight of the displaced fluid*.
The Law of Flotation states that the weight of a floating object is equal to the weight of the fluid it displaces*.
Applications
- Hydrometers: Used to measure the density of liquids
- The Bends: Due to Nitrogen in our blood coming out of solution when the pressure drops, and forming little gas bubbles, which then travel with the blood, and can end up in various joints causing severe pain or brain damage.
Boyle’s Law states that at constant temperature, the volume of a fixed mass of gas is inversely proportional to its pressure*.
Mathematically:
Þ 
Þ 
Mandatory Experiment: To Verify Boyle’s Law, page 112. Then try Exercise 10.4, page 111.
Leaving Cert Physics Syllabus
Content |
Depth of Treatment |
Activities |
STS |
|
|
|
|
Density and Pressure |
Definitions and Units.
Boyle’s Law |
Demonstration of atmospheric pressure, e.g. collapsing can experiment. Appropriate calculations |
Atmospheric pressure and weather.
The “bends” in diving, etc. |
|
Archimedes’ Principle. |
Demonstration only. Calculations not required. |
Hydrometers. |
VERIFICATION OF BOYLE’S LAW
APPARATUS
Boyles’ Law apparatus (see diagram)
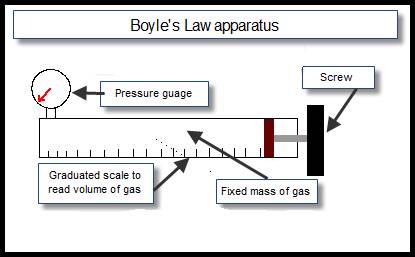
DIAGRAM
PROCEDURE
- The tube is filled with air.
- Note the pressure of the gas from the pressure-gauge and the volume from the graduated scale.
- Turn the screw to decrease the volume and increase the pressure.
- Note the new readings and repeat to get about seven readings.
- Draw a graph of pressure against 1/volume. This should result in a straight line through the origin.
RESULTS
Pressure (Pa) |
|
|
|
|
|
|
|
Volume (m3) |
|
|
|
|
|
|
|
1/volume (m-3) |
|
|
|
|
|
|
|
CONCLUSION
We followed the steps, plotted the graph and did indeed get a straight line through the origin, thus verifying that pressure is inversely proportional to volume.
Whoop-de-doo.
We were just wondering; why do we have to write this up? Why can’t we just put our results into the table as evidence that we did do the actual experiment, then do like the shepherd when he saw the wolves and get the flock out of here?
PRECAUTIONS / SOURCES OF ERROR
- Wait a minute for temperature (and therefore volume) to stabilise after each pressure change before you read the volume.
- Have your eye level with the pressure gauge when taking readings to avoid parallax error.
- Work in a room where the temperature remains constant throughout the experiment (I know - I’m clutching at straws here).
NOTE
Precaution no. 1 is a load of cobblers because the change in volume of air (as a result of it heating up slightly) is negligible in comparison to the error associated with taking the reading itself. However, we continue to include it because it’s what the examiners look for.
Extra Credit
*Archimedes’ Principle states that when an object is immersed in a fluid, the upthrust it experiences is equal to the weight of the displaced fluid.
Both of these concept
s (Archimedes’ Principle and the Law of flotation) should be taken out of the syllabus. They really don’t fit in anywhere and because they are on their own they only cause confusion. But who listens to me?
Sniff L
Upthrust: Look at the sphere which is the liquid in the diagram:
There is a force acting downwards – the weight of the body.
Now if the object is not sinking further then there must be another force opposing the first force
(and equal in magnitude).
This force preventing the object from sinking further is called upthrust.
It is due to the fact that the pressure at the top of the object is less than the pressure at the bottom.
*The Law of Flotation
States that the weight of a floating object is equal to the weight of the fluid it displaces*.
To make sense of this it might help to see where it comes from:
Floating object is not accelerating; implies upward force = downward force (1)
i.e. Upthrust = Weight of floating object (2)
But from Archimedes Principle; Upthrust = Weight of displaced fluid (3)
Equating equations (2) and (3) gives us: Weight of floating object = Weight of fluid displaced.
*Boyle’s Law states that at constant temperature, the volume of a fixed mass of gas is inversely proportional to its pressure.
Here’s a simple activity to demonstrate that pressure affects temperature:
Place the palm of your hand a couple of inches from your mouth, purse your lips and blow; notice how nice and cool it is?
Now do the same thing, except this time ‘haw’ on the hand, i.e. leave your mouth wide open as you expel the air. Notice how much warmer it is.
Now go back to the first stage again, only this time bring your hand right up to your mouth when you blow. This time it seems cool again!
I was going to leave it as an exercise for you to explain how the same air can be at two different temperatures on reaching your hand, but that would be a little disingenuous given that I don’t understand it myself. Obviously it has something to do with pressure, and I think words like ‘adiabatic’ and ‘expansion’ are invoked somewhere along the line, but that’s not an explanation is it?
The point is that pressure, volume and temperature are inexplicably linked, and if you wish to establish a link between any two of them you must keep the third variable constant.
I’ve put up a number of videos on YouTube describing this in more detail. Go to the interactive links page of thephysicsteacher to find them.
Would an astronaut explode in space if they didn’t have a space-suit?
Provided that you do not hold your breath, exposure to vacuum for 5 to 10 seconds is unlikely to produce permanent injury (although it may cause problems in the eardrum).
Some degree of consciousness would be maintained for up to 15 seconds, which is about the time it takes oxygen-deprived blood to go from the lungs to the brain. During this time, the person exposed to the vacuum may become aware of the water on their tongue beginning to boil. As time progresses injury would accumulate as the evaporation of water vapour causes the body to swell and cool. After four minutes they would finally succumb to asphyxia as the brain cannot survive without oxygen. But they would not explode, thanks to the containing effect of the skin and the circulatory system.
The bends
Divers have the opposite challenge to astronauts – how to survive the very high pressures of deep water and then return back to atmospheric pressure at sea level. The gases in the air tanks that divers use to breathe are at high pressure. However, gases that are under high pressure dissolve very easily in water (this is how fizzy drinks are made). This means that if a diver stays in deep water for a long period of time, some of the high pressure nitrogen in the air they are breathing will dissolve in the water in their own body. This becomes a problem if the diver then surfaces too quickly. As the pressure drops the nitrogen comes out of solution and forms painful, and potentially life threatening, bubbles of gas. The only way to avoid getting the bends is to come to the surface slowly, allowing the nitrogen to be released slowly as the pressure gradually decreases.
Things that make you go Hmmmmmmm ….
The Irish scientist Robert Boyle was one of the first to investigate/appreciate atmospheric pressure. He declared that we were all ‘living under a sea of air’.
High pressure is associated with good weather. This is because the ‘blanket of air’ is heavy and it is therefore harder for water molecules to evaporate. There is now less water vapour in the air, so less clouds, which means less rain and more sunlight. So there.
Atmospheric pressure is taken as 100,000 Pa (1 x 105 Pa). Because one Pascal is equivalent to one Newton per square metre, we can say atmospheric pressure is equal to 100,000 Newtons per square metre. Now there are 10,000 square cms in a square metre (100 cm x 100 cm), so therefore one square cm of paper will have a force of 10 Newtons (100,000 divided by 10,000) – equivalent to one kilogram - acting down on it from the atmosphere. Or to make it more realistic, if you draw a square, with each side 10 cm long, that gives you an area of 100 square cm (about the area of the top of your head?), and therefore a force acting downwards (due to atmospheric pressure) of 1,000 Newtons, equivalent to 100 kg. Remember an average student’s weigh would be about 80 kg. And this is acting down on each and every one of us every day!
Apparently we are a couple of cms shorter at night-time than in the morning due to the spine contracting slightly from the weight of our bodies. People who wanted to apply for the Guards, but whose height was borderline, were advised to either get tested in the morning, or lie down during the day until they went for the test!
If you wanted to dive to the bottom of the ocean, you would need to wear a metal suit to prevent getting crushed – see photograph, page 56.
Similarly bottom-dwelling fish could not survive on the ocean surface. Some fish can adapt to the different pressures, but I’m not sure how. Maybe a biology teacher can fill us in?
Aircraft are pressurised, which explains why passengers get ‘sucked out’ of a plane if the door gets blown off at high altitudes.
I recall a quote from Charles Darwin who was describing his extreme discomfort on climbing a particular high-altitude mountain: “I began to bleed through every orifice in my body”.
If a large truck passes you out at speed (if you’re walking or cycling) you can get ‘sucked in’ to its slip-stream.
If you are ever unfortunate enough to be in a car which falls into a lake, and are trying to open the doors, you will not be able to do so until you first let down the window to let in a large amount of water which goes someway to equalising the pressure.
Many liquid containers have two holes which help the liquid to pour out smoothly; one for the liquid out, the other to allow the air to get in without disturbing the flow of liquid. See for example Tetra Pack cartons. Try to empty a two-litre bottle of water and see how long it takes. A much quicker method is to create a ‘mine tornado’ where the air goes up the middle as the water goes down the outside. Quite impressive!
The effect is noticeable if you try to put water into a container which has a small hole on top, like a hot-water bottle! Have you ever tried it? What happens? Would it be any different if you were putting in cold water.See the model of a pair of lungs to demonstrate how we can ‘suck’ up liquids (and air).
Pressure and Boiling Point
Is it true that you can’t make a decent cup of tea up a mountain?
You might think that mountaineers have other things to worry about other than whether they can get a decent cup of tea, but apparently not. As you ascend a mountain, the air pressure decreases and you find yourself gasping for oxygen as well as a nice cuppa. Unfortunately, as the pressure decreases, liquid water finds it easier and easier to turn into a gas, in other words to boil. At sea level, water boils at 100°C but by the time you’ve reached the top of Everest your kettle will boil at just 72°C.
Which is not nearly hot enough to make a decent cup of cha’.
Exam Questions
- [2010 OL]
A concrete mixer delivered 50 m3 of concrete to a building site, what was the mass of the concrete delivered?
(Density of concrete = 2400 kg m−3)
- [2006][2002 OL][2005 OL][2007 OL][2009 OL]
Define pressure.
- [2002 OL][2005 OL]
Give the unit of pressure.
- [2006]
Is pressure a vector quantity or a scalar quantity? Justify your answer.
- [2002 OL][2005 OL]
Name an instrument used to measure pressure.
Mathematical pressure
- [2002 OL]
The wind exerts a horizontal force of 1000 N on a wall of area 20 m2. Calculate the pressure at the wall.
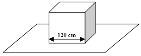[2008 OL]
A solid block in the shape of a cube of length 120 cm rests on a table. The weight of the block is 25 N. Calculate the pressure it exerts on the table.
- [2005]
A container contains 5.0 kg of water. If the area of the base of the container is 0.5 m2.
Calculate the pressure at the base of the container due to the water.
P = F/A = [ (5.0)(9.8)/(0.5)] Þ P = 98 Pa
- [2005 OL]
- The African elephant is the largest land animal.
An elephant weighs 40 000 N and is standing on all four feet each of area 0.2 m2.
Calculate the pressure exerted on the ground by the elephant.
- Why would the pressure on the ground be greater if the elephant stood up on just two feet?
- [2008]
The head of a thumbtack has an area of 500 mm2. Its point has an area of 0.3 mm2. The pressure exerted at the head of the thumbtack is 12 Pa. What is the pressure exerted at the point of the thumbtack?
-
Atmospheric Pressure
[2005 OL][2007 OL]
Describe an experiment to show that the atmosphere exerts pressure.
[2002 OL]
When air is removed from the metal container shown in the diagram, it collapses. Explain why.
- [2005 OL]
The earth is covered with a layer of air called the atmosphere.
What holds this layer of air close to the earth?- [2005 OL]
The type of weather we get depends on the atmospheric pressure.
Describe the kind of weather we get when the atmospheric pressure is high.
Pressure in a liquid
- [2009 OL]
Describe an experiment to show that the pressure in a liquid increases with depth.
- [2006 OL]
Which one of the following instruments can be used to measured the density of a liquid?
barometer hydrometer thermometer- [2007][2010 OL]
State Archimedes’ principle.
- [2008]
State the law of flotation. - [2004]
A can of height 10 cm is submerged in water. What is the difference in pressure between the top and bottom of the can?
- [2009 OL]
A diver is swimming at a depth of 5m. He then dives deeper until he reached a depth of 30 m. Calculate the increase in pressure on the diver at this new depth
(p = ρgh ; density of water = 1000 kg m−3 ; g = 9.8 m s−2)Boyle’s Law
- [2009] [2006][2005][2003 OL][2007 OL] [2010 OL]
State Boyle’s law
[2007 OL]- A balloon rises through the atmosphere while the temperature remains constant.
The volume of the balloon is 2 m3 at ground level where the pressure is 1000 hPa.
Find the volume of the balloon when it has risen to a height where the atmospheric pressure is 500 hPa.- What will happen to the balloon as it continues to rise?
- [2006]
- A small bubble of gas rises from the bottom of a lake. The volume of the bubble increases threefold when it reaches the surface of the lake where the atmospheric pressure is 1.01 × 105 Pa. The temperature of the lake is 4 oC. Calculate the pressure at the bottom of the lake.
- Calculate the depth of the lake.
-
Mandatory Experiment
[2004 OL]
In an experiment to verify Boyle’s law, a student measured the volume of a gas at different pressures.
The table shows the measurements recorded by the student.
Pressure /kPa100
111
125
143
167
200
250
Volume /cm3
5.0
4.5
4.0
3.5
3.0
2.5
2.0
1/Volume /cm-3
0.25
- Draw a labelled diagram of the apparatus used in this experiment.
- Copy this table and fill in the last row by calculating 1/ volume for each measurement.
- Plot a graph on graph paper of pressure against 1/volume.
- Explain how your graph verifies Boyle’s law.
- Give one precaution that the student took in carrying out the experiment.
- [2003]
In an experiment to verify Boyle’s law, a student measured the volume V of a gas at different values of the pressure p.
The mass of the gas was not allowed to change and its temperature was kept constant.
The table shows the data recorded by the student.
p/ kPa120
180
220
280
320
380
440
V/cm3
9.0
6.0
5.0
4.0
3.5
3.0
2.5
- Describe with the aid of a diagram how the student obtained this data.
- Draw a suitable graph on graph paper to show the relationship between the pressure of the gas and its volume.
- Explain how your graph verifies Boyle’s law.
- Describe how the student ensured that the temperature of the gas was kept constant.
Exam Solutions
- m = 2400 × 50 = 120000 kg
- Pressure = Force ÷ area.
- The unit of pressure is the pascal.
- It is a scalar because it has no direction.
-
Mathematical pressure
The barometer.- P = F/A = 1000/20 = 50 Pascals.
- P = F/A Þ P = 25 ÷ (1.2)2 Þ P = 17.4 pa
- P = F/A = [ (5.0)(9.8)/(0.5)] Þ P = 98 Pa
- P = F/A Þ P = 40 000/0.8 Þ P = 5,000 Pa.
- The area would be smaller.
- (at head:) F = P × A Þ F = 12(500 × 10-6) Þ F = 6.0 × 10-3 N
Note that the force is constant throughout.
(at point:) P = F/A = (6.0 × 10-3) / 0.3 × 10-6) = 2.0 × 104 PaAtmospheric Pressure
- Apparatus: glass of water and cardboard.
Procedure: place cardboard over glass and invert.
Observation/conclusion: water remains in glass.- The pressure outside (due to atmospheric pressure) is greater than the pressure inside.
- Gravity.
- Good weather, dry, clear skies, little wind, settled.
Pressure in a liquid
- Set up as shown.
Note that the water coming out of the hole at the bottom travels the farthest because it is under the greatest pressure.
- Answer: hydrometer
- When an object is immersed in a fluid, the upthrust it experiences is equal to the weight of the displaced fluid.
- When a body floats in a liquid its weight is equals the weight of fluid displaced.
- P = ρgh Þ P = (1000)(9.8)(0.1) = 980 Pa
- Pressure at 30 m: (p = ρgh = (103)(9.8)(30) =) 2.94 ×105 Pa
Pressure at 5 m: (p = ρgh = (103)(9.8)(5) =) 0.49 ×105 Pa
Increase in pressure at 30 m: =2.94 ×105 – 0.49 ×105 = 2.45 ×105 PaBoyle’s Law
- Boyle’s Law states that Pressure is inversely proportional to volume for a fixed mass of gas at constant temperature.
- (P1V1 = P2V2) Þ 1000 × 2 = 500 × V2. Þ V2 = (1000 × 2)/500 = 4 m3.
- It will continue to expand
- Pressure at bottom = 3 × pressure at top = 3.03 × 105 Pa)
- Ridiculously tricky one this; you need to consider just the effect of the water so to get rid of the effect of the atmosphere you must ignore the 1.01 × 105 Pa (the pressure of the atmosphere).
Pressure at bottom due to water = 2.02 × 105 Pa
P= ρgh
h = P/ρg = 2.02 × 105 / (1.0 × 103)( 9.8 ) = 20.61 m
-
Mandatory Experiment
- See diagram.
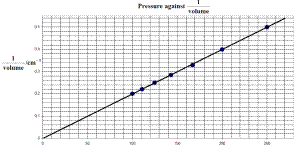See table
Pressure /kPa
100
111
125
143
167
200
250
Volume /cm3
5.0
4.5
4.0
3.5
3.0
2.5
2.0
1/Volume /cm-3
0.20
0.22
0.25
0.28
0.33
0.40
0.50
- See graph
- A straight line through the origin shows that pressure is proportional to 1/volume
- After changing pressure wait a short time before taking readings / read the volume scale at eye level.
- See diagram.
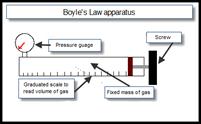Note the pressure of the gas from the pressure-gauge and the volume from the graduated scale.
Turn the screw to decrease the volume and increase the pressure.
Note the new readings and repeat to get about seven readings.p/ kPa
120
180
220
280
320
380
440
1/V/cm-3
0.111
0.167
0.200
0.250
0.286
0.333
0.400
Axes labelled
6 points plotted correctly
Straight line
Good fit- A straight line through the origin verifies that pressure is inversely proportional to volume
- Release the gas pressure slowly, allow time between readings.
Source : http://www.thephysicsteacher.ie/LC%20Physics/Student%20Notes/10.1%20Pressure.doc
Web site link: http://www.thephysicsteacher.ie
Author : not indicated on the source document of the above text
Density and pressure
Density and pressure
Density and pressure
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Density and pressure mean ? Which is the meaning of Density and pressure?
Density and pressure physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us
