Dynamics
Dynamics
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Dynamics
Dynamics Notes
Dynamics is the study of forces.
Newton’s First Law of Motion, the law of inertia, states that an object at rest will remain at rest and an object in motion will remain in motion with a constant velocity (straight line motion with the same speed) unless acted on by a net external force.
Newton’s Second Law of Motion is most easily stated as an equation
S F = ma
which is that the net force (the sum of all the forces) on an object equals the object’s mass times the acceleration.
You should always start these problems by drawing a Free Body Diagram (FBD) by drawing vectors for each force acting on the object.
In many problems, you will need to resolve the forces in components by doing F=ma for the horizontal values and F=ma for the vertical values.
Newton’s Third Law of Motion- Forces always occur in equal and opposite pairs. If object A exerts a force on object B, object B exerts and equal and opposite (direction) force on object A.
It’s important to note here that the pair of forces act on different objects, so they do not cancel each other.
Weight versus Mass
Mass is a measure of the amount of matter in an object.
Weight, on the other hand, is the amount of force that pulls on you due to the gravity on Earth, or some other massive object.
Since weight is a force, we look to F=ma and we find that Weight= mg, or
W=mg
Our awareness of weight comes from the forces that balance it. This force, called apparent weight, is the weight that you feel. It depends on your circumstances (where you are, how you’re accelerating, etc). If there is no force to balance your weight, that state is called weightlessness.
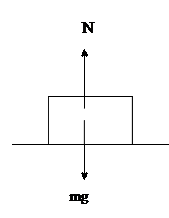

Normal Force (N) is a supporting force which pushes an object perpendicular to the surface that it rests on. In the above picture, the surface is horizontal, so the normal force pushes upward.
If the above block is at rest,
S Fy = may
N – mg = 0
N = mg
Note that the coordinate system has been set up in the standard way (up is +y, right is +x) Since I used a negative sign to state that mg was downward, I do not need to include the negative in g = 9.8 m/s2.
The normal force will not always be equal to mg, however.
Take a case where you (m = 80 kg) are standing on an elevator, moving upward and decelerating with a magnitude of 8 m/s2. First we establish our coordinate system so that up is positive
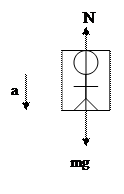

S Fy = may
N – mg = m (-8)
N = mg + m(-8) = (85)(9.8 – 8) = 144 N
Or take a case where there is a block being moved on the floor with a rope of tension, T.
T


If the above block stays on the ground
S Fx = max S Fy = may
T cos q = max N + Tsin q -mg = 0
ax =
Inclined Planes
For inclined plane problems, you should establish your coordinate system so that the x axis is aligned with the incline plane and the y axis is perpendicular to the plane.
![]()
![]()
![]()
![]()


S Fx = max S Fy = may
![]() mg sinq = max N - mg cosq = 0
mg sinq = max N - mg cosq = 0
Many other problems (pendulum hanging backwards or forward in an accelerating train, sign hanging at rest from multiple wires at different angles) can all be solved simply in similar ways by choosing a coordinate system and breaking up your vectors into x and y components.
Systems with multiple objects
In pulley systems and other systems with multiple bodies, you can either treat the objects as one system and one FBD or treat them each individually with a FBD for each object.

To find the acceleration of the blocks, I would treat the boxes as one system (because they all have the same acceleration) so that T1 is pulling all of the masses.

S F = ma
T1 = (M1 + M2 + M3) a
To find the tension in T2 and T3, however, we could draw a FBD for each block.

S F = ma S F = ma
T3 = M3a T2 – T3 = M2a
Or, we could treat M1 and M2 as one system and get
S F = ma
T2 = (M2 + M3) a
Pulleys:
Atwood Machine
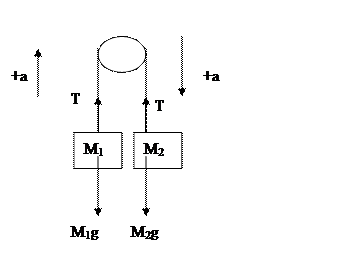

You first need to draw your FBD for each mass. Let’s assumer that M2 is heavier (if we assume wrong, we will end up with a negative acceleration at the end). Next we need to establish our coordinate system. Since the blocks have the same acceleration and tension, and M1 is going up while M2 is going down we need to rotate our coordinate system so that both accelerations have the same sign.
S F = ma S F = ma
T - M1g = M1a M2g - T = M2a
OR: If you treat the blocks as one system:
S F = ma
M2g – M1g = (M1 + M2)a
You can use this process for many different pulley type problems.
Friction
Static friction is the friction between objects at rest. The static friction force can vary from 0 to some maximum force depending on the situation.
Kinetic (sliding) friction is the friction between objects that are moving
0 < fs ![]() msN (static friction)
msN (static friction)
fk = mkN (kinetic friction)
f= friction force m = coefficient of friction N = normal force
Note that the area of contact doesn’t affect the friction force
Please make sure that you calculate the normal force using F=ma. Don’t just assume that it is mg, because in many cases, it won’t be.
Circular Motion
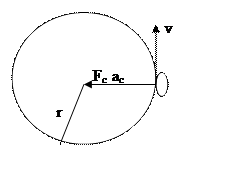

If an object is traveling in a circle, then the velocity isn’t constant. That means that there is an acceleration inward, which means that there is a net force inward.
The Centripetal Force, Fc isn’t a force on its own; it is always the resultant force of all of the forces in that direction.
Fc = mv2/r so ac = v2/r
For instance, take a rollercoaster loop. At the top of the loop:
S F = ma
-N –mg = m( -v2/r)
at the bottom of the loop
S F = ma
N –mg = mv2/r
Somewhere in the middle of the loop, you need to sum the forces in the x and y direction
S Fx = max S Fy = may
Nx = mv2/r Ny -mg = 0
N2= Nx2 + Ny2
Banked Curves


In banked curve problems, you need to set your coordinate system such that x is horizontal and y is vertical. (This is different than normal inclined planes, where x is aligned along the plane because the centripetal force is horizontal.)
S Fx = max S Fy = may
Nsinq = mv2/r N cosq -mg = 0
These equations apply for a banked curve without friction. In these cases, there is some minimum velocity that the car has in order to stay in its circle without slipping downward.
If friction is involved, its direction is dependent on the situation.
For instance, if the car is traveling faster than the minimum velocity (explained above), then it has a tendency to move upwards on the slope, so the friction acts down the slope.
If the car is traveling slower than the minimum velocity, then the car has a tendency to slip down the slope, so friction must act up the slope.
Draw the free body diagram with friction, resolve it into x and y components and solve as usual.
If you don’t know whether or not the velocity is faster or slower than the minimum velocity, then just arbitrarily choose a direction for the friction and solve. If you find that the friction is positive, then you choose your direction correctly. If the frictional force is negative, then you choose the wrong direction.
Drag Force - A retarding force that tends to reduce the speed of an object. As an object falls, air resistance is the drag force.
Fd = bv2 for high speeds
Fd = bv for low speeds
b is drag constant, which would be determined by the object and the fluid through which it is moving.
While falling, the object’d FBD produces the equation:
mg – Fd = ma
At terminal velocity, the object’s drag force equals the objects weight.
Fd = mg
This, of course, means that there is no net force, thus no acceleration, so the object isn’t speeding up or slowing down, but instead continuing with a constant (terminal) velocity.
Hook’s Law
When a spring is stretched or pushed, it exerts a force opposite to the direction of the stretched determined by the properties of the spring and the distance the spring stretches.
Fspring = - kx
x is the distance the spring is stretched from equilibrium.
k is the spring constant. It’s units would be _____
There is a negative sign in the equation to let you know that the force is in the opposite direction of the displacement (the force isn’t necessarily negative!). When you use this equation in your Fnet= ma set-up, please look at the direction of the forces to determine if Fs should be positive or negative.
Source : http://www.groovytoo.com/robinson/AP/dynamics%20notes.doc
Web site link: http://www.groovytoo.com/robinson/
Author : Ms. Robinson
Dynamics
Dynamics
Dynamics
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Dynamics mean ? Which is the meaning of Dynamics?
Dynamics
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us