• 

 

Effects of an electric current

 

 

---

 

Effects of an electric current

 

The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.

We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge

Physics

 

Effects of an electric current

 

Three effects of an Electric Current

 

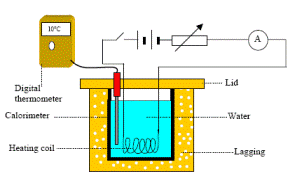
• Heating Effect Demonstrate with an electric coil in beaker of water plus thermometer.
• Magnetic Effect* Demonstrate with an electromagnet (connected up to source of electricity).
• Chemical Effect Demonstrate with a voltameter (see below).

 

Relationship between Work, Current, Resistance and Time

 

 

Now Power is defined as the rate at which work is done, i.e. Power = Work/time, so Power = I2R
This is known as Joule’s Law

 

Joules Law states that the rate at which heat is produced in a conductor is proportional to the square of the current, provided its resistant is constant.       

 

 

The Chemical Effect of an Electric Current: the voltameter

You must know the meaning of each of the following as they relate to the diagram.

 

Applications of the Chemical Effect of a Current

 

Why is Electrical Energy transmitted using high voltage power lines?*
We have seen that the heat produced by an electric current is given by the formula P =  I2R.
This means that a large current will produce a lot of heat energy. This is a waste of energy and therefore should be minimised if possible.
Now we also know that P = VI, which means we can halve the current if we double the voltage.
In practice we make the current very small by making the voltage very large (e.g. 300 kVolts) when electrical energy is being carried across the countryside.

 

Domestic Electric Circuits

 

 

 

 

 

 

 

 

 

 

 

 

            3-Pin plug with fuse                Miniature Circuit Breakers (MCB)      Residual Current Devices (RCD)

 

 

 

The kiloWatt hour (kWhr)

The kiloWatt hour is the unit of energy used by the ESB.
One kiloWatt hour is the amount of energy used by a 1000 Watt appliance in one hour.

Rule: Number of kiloWatt hours = Number of kilowatts × Number of Hours.

 

Relationship between Current and Voltage for different conductors
You must be able to draw a graph for each of the following, list the charge carriers in each case, and explain the shape of each graph.
Note that in this case we are not looking to obtain a value for the slope of the graph, and therefore we put the independent variable (Voltage) on the X-axis.

Conductor	Graph	Charge Carriers	Explanation
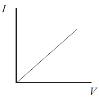
A Metallic conductor		Electrons	As the p.d. is increased, the current increases proportionally.
A Filament Bulb		Electrons	As current increases, the wire heats up, Þresistance increases, Þcurrent does not rise as rapidly.
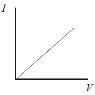
Ionic solutions (active electrodes)		Positive ions, Electrons	Copper ions discharged at the cathode are replaced by Copper atoms entering the Solution as ions in the anode.
Ionic solutions (inactive electrodes)	I     V	Positive ions, Electrons	Oxygen is produced at the Anode. This combines with the Platinum to become a ‘cell’ which opposes the driving current and  has to be overcome.
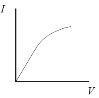
Gases	I                           V	Positive ions, Electrons	Stage one – Normal Stage two – Saturation Stage Three – Avalanche Effect
Vacuum	I                          V	Electrons	Stage one – Thermionic emission Stage two - saturation
Semiconductors		Positive holes, Negative electrons	See chapter 25 for a detailed explanation

Mandatory Experiments

• To Investigation the variation of current (I) with p.d. (V) for Copper electrodes with Copper Sulphate solution
• Joule’s Law Experiment*

 

Content	Depth of Treatment	Activities	STS
6. Effects of electric current	Heating: W = I 2Rt Chemical effect – an electric current can cause a chemical reaction. Magnetic effect of an electric current.	Demonstration of effect. Appropriate calculations. Demonstration of effect. Demonstration of effect.	Everyday examples. Advantage of use of EHT in transmission of electrical energy. Uses of the chemical effect. Everyday examples.
7. Domestic circuits	Plugs, fuses, MCBs (miniature circuit breakers). Ring and radial circuits, bonding, earthing, and general safety precautions. RCDs (residual current devices). No drawing of ring circuits required.	Wiring a plug. Simple fuse calculations.	Electricity at home • fuse box • meter, etc. Electrical safety.
	The kilowatt-hour. Uses.	Appropriate calculations.
3. Conduction in materials	Conduction in • metals • ionic solutions (active and inactive electrodes) • gases • vacuum • semiconductors References in each case to charge carriers.	Interpretation of I–V graphs.	Neon lamps, street lights.

Leaving Cert Physics Syllabus

TO VERIFY JOULE’S LAW
APPARATUS:
Calorimeter with a lid, heating coil, power supply, rheostat, ammeter, thermometer, stopwatch, electronic balance.

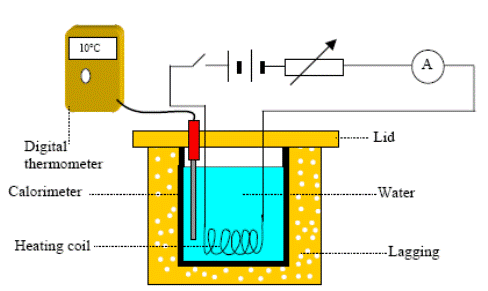DIAGRAM:

 

 

 

 

 

 

 

PROCEDURE:

• Set up the circuit as shown.

 

• Note the temperature.

• Switch on the power and simultaneously start the stopwatch.

 

• Make sure the current stays constant throughout; adjust the rheostat if necessary.

• Note the current using the ammeter and note the time for which the current flowed using the stopwatch.

 

• Stir and note the highest temperature. Calculate the change in temperature (θΔ)

• Repeat the above procedure for increasing values of current I, taking at least six readings.

 

• Plot a graph of I2 (y-axis) against θΔ (x-axis).

RESULTS:

 

CONCLUSION:
A graph of our results produced a straight-line through the origin thus verifying that Δθ α I2  and therefore verifies  Joule’s law.

 

PRECAUTIONS:

• Put sufficient water in the calorimeter to cover the heating coil.
• Take care not to exceed the current-rating marked on the rheostat and/or the calorimeter.

NOTES

• See the note in the text-book to see how this experiment (where Δθ α I2) verifies Joule’s Law (P α I2).
• Allow the coil to heat the water for about five minutes. This must be the same for each run.

TO INVESTIGATE THE VARIATION OF CURRENT (I) WITH P.D. (V) FOR COPPER ELECTRODES IN A COPPER-SULPHATE SOLUTION

APPARATUS:
Low voltage power supply, rheostat, voltmeter, ammeter, copper electrodes in a copper-sulphate solution.

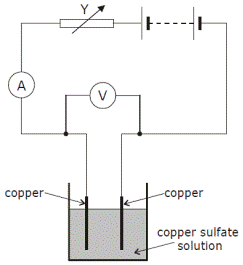
DIAGRAM:

 

 

 

 

 

 

 

PROCEDURE:

• Set up the circuit as shown.

• Record the potential difference (V) and the current (I) using the voltmeter and ammeter respectively.

 

• Adjust the rheostat to obtain different values for V and I.

• Obtain at least six values for V and I.

 

• Plot a graph of I against V.

 

RESULTS:

V (V)
I (A)

 

CONCLUSION:

• We obtained a straight line through the origin therefore the current through the copper-sulphate solution is proportional to the potential difference across it.
• We believe our results to be reliable because they resulted in a straight line through the origin, as the theory predicted.

SOURCES OF ERROR:

• The copper-sulphate solution may not be concentrated enough.
• The copper electrodes may have become oxidised and will no longer conduct.

 

PRECAUTIONS:

• Sand the electrodes beforehand.

 

NOTES

This is one of the few experiments which actually works very well, so take your time and get it right.

• Get a 250 ml beaker.

 

• Clean it !!

• Grab a pair of electrodes form the box.

 

• Sand them well, until both are shiny.

• Separate the copper electrodes by putting a rubber bung between them, and secure the set-up with an elastic band (all supplied).

 

• Place in the 250 ml beaker.

• Shake the container of Copper Sulphate solution well.

 

• Slowly pour the solution into the beaker (using the funnel) until it is at roughly the 150 ml level. Any higher and it might come in to contact with the crocodile clips and short-circuit (can you see how?).

• Set up the circuit as shown in the diagram. Using the rheostat is optional as you could just use the dial on the power-supply to vary the voltage (p.d.), and therefore the current. The advantage of using the rheostat is that you can control it to give you nice even numbers for the voltage, the disadvantage is that it can be a pain in the ass to set-up. So no prizes for guessing what most of you are going to choose.

 

• Now follow the conventional instructions: Take the readings, plot the graph, blah blah blah (remember none of this goes in your report!)

• Remember to take apart the apparatus and put them back in the containers supplied.

 

• Please ??

 

 

Notes for teachers:

• The copper-sulfate solution may be made by adding 15 g of copper-sulfate to 100 cm3 of warm water. Adding 2 cm3 of concentrated sulphuric acid ensures that the solution stays clear and this will enable it to be reused a number of times.

• A varying voltage can be obtained from a fixed supply voltage by using a potential divider. It consists of a variable resistor or fixed resistors in series. Move the slider to change the output voltage. This results in the output voltage from the potential divider being a fraction of the input voltage.

Extra Credit
*Magnetic Effect of an Electric Current
One interesting application of the magnetic affect is the Levitating Trains which are used in Japan. In order to generate a large magnetic field, large currents are needed, but because of resistance in the line, this can get very expensive. To get around this, engineers make use of something called SUPERCONDUCTIVITY; this is where the resistance of the metal drops to zero, resulting in very large currents and therefore very large magnetic fields.
The problem with this is that the superconducting metals must be very, very cold, and keeping the metals this cold can get very, very expensive.

 

*W  = I2 Rt
Let’s rewind here just a little.
We know (don’t we?) that heat is a form of energy, and energy is the ability to do work.
We also know that any time work is being done, energy is being converted from one form to another.
It turns out that about 250 years ago, scientists were aware of all these different forms of energy, but weren’t aware that all these different energies were equivalent.
One of the scientists who changed all this was a man called James Joule.
Among other things, he discovered that;
W  µ I2                        if t and R are fixed
W µ R             if I and t are fixed
W µ t              if I and R are fixed

From this it follows that W  µ I2 Rt ,  Þ  W = k I2 Rt , where k is a constant.
It turns out (because of how we define the other variables) that k =1.
Therefore W  = I2 Rt
And Power P = I2 R     (because Power is work divided by time)

Note that we can also obtain this formula starting with the formula for electrical power and then using Ohm’s Law:
P = VI, and V = IR Þ P = (IR) R Þ P = I2 R

*Why is Electrical Energy transmitted using high voltage power lines?
In practice we make the current very small by making the voltage very large (e.g. 300 kVolts) when electrical energy is being carried across the countryside.

These voltages are then lowered before they enter a town, using transformer stations, and are lowered even more (to 220 volts) using a transformer outside your house. Every three or four houses have their own transformer. Now each time the voltage is lowered, the current is raised, but now at least it’s only for a short distance.
Many of your electrical appliances have transformers inside then which reduce the voltage further still, often to as low as nine of twelve volts. These appliances can also probably use batteries.
A few further points of interest:
While the current running through the power-lines is small, it may still be enough to heat the wire slightly. I am reliably informed that this is why birds prefer to sit on power-lines rather than on branches!
If you are passing under a high voltage line you may notice a slight hiss. This is because the high voltages are ionising the air around them.

Electricity and Death
The hazards of electricity (see table below) depend on the amount of electrical current, its frequency, its duration, its path through the body, and the physical condition of the person.
Alternating current at 60 Hz is slightly more dangerous than direct current, but high frequency currents (greater than a few kHz) are safer because they tend to flow on the surface of the skin and away from the heart and lungs.
The resistance of the body varies from about 300 ohms to about 100,000 ohms, and thus even very low voltages can produce lethal shocks.
Fatalities have occurred at voltages as low as 24 volts.
For currents that exceed the "let-go" current (10-20 mA) the person becomes frozen to the circuit, and the current typically rises to a level of about 25 mA where muscular contractions onset.
Then the person is either thrown clear of the circuit or the current continues to rise until ventricular fibrillation or cardiac arrest occurs (at 50-200 mA), assuming the path of the current is through the heart.
Pulsed currents such as one might encounter with the discharge of a Van de Graaff generator or other charged capacitance present special considerations.
One can endure currents that would otherwise be lethal if the duration is short enough. For pulses of less than a few seconds duration, the relevant quantity is the square of the current integrated over the time of the pulse.
Values of I2t greater than about 0.01 A2- sec can cause electrocution for a typical adult.
For a reasonably low body resistance of 2000 ohms, this translates into an energy of about 10 joules.
Severe shocks can occur at levels 10-100 times lower and can startle one into an accident, since it is natural to jerk away from such a shock.
Good practice entails standing on an insulated surface and keeping one hand in a pocket or behind one's back while working around high voltage.
In performing electrical demonstrations, one should ideally have a knowledgeable assistant trained in cardiopulmonary resuscitation (CPR) always present.
The probability of resuscitating someone is good if CPR is begun within three minutes but becomes poor after about six minutes.

Average Effects of Continuous ac or dc Electrical Currents on Healthy Adults

 

Why historically do we in Europe use electricity at 240V 50Hz, whereas US for example uses 110V 60 Hz?
Ans:
The voltage is a trade off issue; 220V is more likely to electrocute, but the lower current means that fewer people die from fires caused by overheated cables. 
Frequency issue is more technical as far as I can remember.

Note that all building sites must use 110 Volts, that’s why you see those yellow boxes (transformers) attached to all heavy-duty equipment.
However they should also be using heavy-duty cable (i.e. large diameters) to absorb the extra heat given off.

*To Verify Joule’s Law
Joule’s Law states that the rate at which heat is produced is proportional to current squared.
In this experiment we show that change in temperature (rq) is proportional to current squared (I2), which isn’t quite the same thing.
The assumption is that heat produced is directly proportional to change in temperature (RWP does refer to this on page 276) Þ  if rq  is proportional to I2 , so too  must the Heat Produced be proportional to I2 .

Before carrying out the experiment you should try Question 2, page 107 of the workbook (part (a) only).
You should also be in a position to answer the questions at the bottom of page 276 of the textbook.

Mnemonics:   

• V = IR: Very Intelligent Rachel                     
• P = VC: (PVC) (Power = Voltage x Current)

Exam Questions

• [2006 OL]

Give one use for electricity in the home.

  

• [2004 OL][2008 OL][2010]

List three effects of an electric current.

• [2002][2004 OL]

Describe an experiment that demonstrates the heating effect of an electric current.

• [2004 OL]

State two factors on which the heating effect of an electric current depends.

• [2003 OL]

Hans Oersted discovered the magnetic effect of an electric current in 1820 while demonstrating electricity to his students. Describe how you would demonstrate the magnetic effect of an electric current.

  

• [2005]

Explain why high voltages are used in the transmission of electrical energy.

• [2002]

Suggest a method of reducing the energy “lost” in ESB power lines.

• [2002]

The ESB supplies electrical energy to an industrial park from a local power station
Total resistance of the cables = 9.6 W. Current flowing in the cables= 200 A
Calculate the rate at which energy is “lost” in the cables.

• [2006]

What is the resistance of the filament of a light bulb, rated 40 W, when it is connected to the mains?

  

 

• [2004 OL][2005 OL][2007 OL]

Name two safety devices that are used in domestic electric circuits.

• [2006 OL]

What is the colour of the earth wire in an electric cable?

• [2009 OL]

What is the colour of the wire that should be connected to the fuse in a plug?

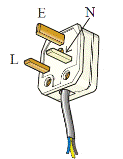
• [2003 OL]

Give the standard colour of the insulation on the wires connected to each of the terminals L, N and E on the plug in the diagram.

• [2003 OL]

What is the purpose of the wire connected to the terminal E on the plug?

• [2004] [2008 OL]

Name and give the colour of the wire that should be connected to the fuse in a standard three-pin plug.

• [2006 OL]

Give one safety precaution that should be taken when wiring a plug.

• [2003 OL][2009 OL][2010 OL]

Explain why a fuse is used in a plug.

• [2009 OL]

Explain how a fuse works.

• [2006 OL]

What will happen when a current of 20 A flows through a fuse marked 13 A?

• [2009 OL]

Why would it be dangerous to use a fuse with too high a rating?

• [2004]

Explain why replacing a fuse with a piece of aluminium foil is dangerous.

• [2006 OL]

Name a common material used to conduct electricity in electric cables.

• [2004]

A table lamp has a power rating of 100 W. What is the most suitable fuse for the lamp?

• [2009 OL]

Plugs are used to connect electrical appliances in the home to the 230 volt ESB supply.
Modern plugs contain a small fuse which comes with a rating of 1A, 2A, 3A, 5A or 13A.
A coffee maker has a power rating of 800 W.
What is the most suitable fuse to use in the plug of the coffee maker?

• [2003 OL]

A kettle has a power rating of  2 kW when connected to the ESB mains voltage of 230 V.
Calculate the current that flows when the kettle is first plugged in.

• [2003 OL]

The fuse in the plug of the kettle in the previous question was replaced with a 5 A fuse
This current will only flow for a very short time. Explain why.

• [2004][2006 OL]

Some electrical appliances are supplied with two-pin plugs.
Why is an earth wire not required in these devices?

• [2006 OL]

Why is the coating on electric cables made from plastic?

• [2008]

A toaster has exposed metal parts. How is the risk of electrocution minimised?

• [2003 OL][2010 OL]

Bonding is a safety precaution used in domestic electric circuits.
How does bonding improve safety in the home?

 

  

• [2009 OL]

Name another device with the same function as a fuse.

• [2003][2002 OL][2010 OL]

What is the purpose of a miniature circuit breaker (MCB) in an electric circuit?

• [2009][2010 OL]

When will an RCD (residual current device) disconnect a circuit?

• [2006]

An RCD is rated 30 mA. Explain the significance of this current.

• [2004][2002]

What is the purpose of a residual current device (RCD) in an electrical circuit?

• [2003 OL]

Name a device that is often used nowadays in domestic electric circuits instead of fuses.

• [2004]

Give one advantage of a Residual Current Device (RCD) over a Miniature Circuit Breaker (MCB).

  

• [2008]

What are the charge carriers when an electric current passes through an electrolyte?

• [2003]

Draw a graph to show the relationship between current and voltage for a metal at constant temperature

• [2003]

How would the VI graph for a metal differ if its temperature were increasing?

• [2003]

Draw a graph to show the relationship between current and voltage for an ionic solution with inactive electrodes

• [2003]

How would the graph for the ionic solution differ if its concentration were reduced?

• [2003]

Draw a graph to show the relationship between current and voltage for a gas.

 

  

• [2004 OL]

What is the kilowatt-hour?

• [2006 OL]

What is the function of the ESB meter?

•  [2004 OL]

Calculate the cost of using a 2 kW electric heater for 3 hours at 10 cent per kilowatt-hour.

• [2009 OL]

The electrical energy supplied by ESB to the home is measured in kWh (kilowatt-hour).

• A coffee maker has a power rating of 800 W.

If the coffee maker was in use for 150 minutes calculate the number of units of electricity used by the coffee maker.

• Calculate the cost of the electricity used if each unit costs 15 cent.

 

Mandatory Experiments

• [2007 OL]

In an experiment to verify Joule’s law, a heating coil was placed in a fixed mass of water.

I/A	1.0	1.5	2.0	2.5	3.0	3.5	4.0
I 2/A2			4
Δθ/°C	2.2	5.0	8.8	13.8	20.0	26.0	35.2

A current I was allowed to flow through the coil for a fixed length of time and the rise in temperature Δθ was recorded. This was repeated for different values of I.
The table shows the data recorded.

• Draw a labelled diagram of the apparatus used.
• How was the current changed during the experiment?
• Copy the table and complete it in your answerbook.
• Using the data in the completed table, draw a graph on graph paper of Δθ against I2.

Put I2 on the horizontal axis (X-axis).

• Explain how your graph verifies Joule’s law (Δθ α I2).
• [2006]

In an experiment to verify Joule’s law a student passed a current through a heating coil in a calorimeter containing a fixed mass of water and measured the rise in temperature Δθ for a series of different values of the current  I. The student allowed the current to flow for three minutes in each case.

• Describe, with the aid of a labelled diagram, how the student arranged the apparatus.
• Why was a fixed mass of water used throughout the experiment?
• The student drew a graph, as shown. Explain how this graph verifies Joule’s law.
• Given that the mass of water in the calorimeter was 90 g in each case, and assuming that all of the electrical energy supplied was absorbed by the water, use the graph to determine the resistance of the heating coil.

The specific heat capacity of water is 4200 J kg–1 K–1.

 

• [2003]

In an experiment to verify Joule’s law, a heating coil was placed in a fixed mass of water.
The temperature rise Δθ produced for different values of the current I passed through the coil was recorded.

I /A	1.5	2.0	2.5	3.0	3.5	4.0	4.5
Δθ / °C	3.5	7.0	10.8	15.0	21.2	27.5	33.0

In each case the current was allowed to flow for a fixed length of time.
The table shows the recorded data.

• Describe, with the aid of a labelled diagram, how the apparatus was arranged in this experiment.
• Using the given data, draw a suitable graph on graph paper and explain how your graph verifies Joule’s law.
• Explain why the current was allowed to flow for a fixed length of time in each case.
• Apart from using insulation, give one other way of reducing heat losses in the experiment.

 

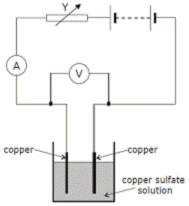• [2004 OL]

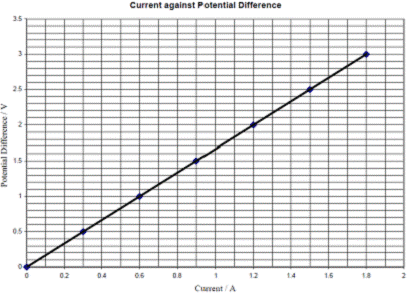
The diagram shows a circuit used to investigate the variation of current with potential difference for a copper sulfate solution.

• Name the instrument used to measure the current.
• How was the potential difference measured in the experiment?
• Name the apparatus Y and give its function in the experiment.
• The following table shows the values recorded for the current and the potential difference during the experiment.

Potential Difference /V	0	0.5	1.0	1.5	2.0	2.5	3.0
Current /A	0	0.3	0.6	0.9	1.2	1.5	1.8

 

 

Using the data in the table, draw a graph on graph paper of the current against the potential difference. Put current on the horizontal axis.

• Calculate the slope of your graph and hence determine the resistance of the copper sulphate solution.

 

• [2002]

V /V	0.5	1.0	1.5	2.0	2.5	3.0	3.5	4.0	4.5	5.0
I /mA	24	48	79	102	120	143	185	195	215	263

In an experiment to investigate the variation of current I with potential difference V for a copper sulfate solution, the following results were obtained.

• Draw a diagram of the apparatus used in this experiment, identifying the anode and the cathode.
• Draw a suitable graph on graph paper to show how the current varies with the potential difference.
• Using your graph, calculate the resistance of the copper sulfate solution. (Assume the resistance of the electrodes is negligible.)
• Draw a sketch of the graph that would be obtained if inactive electrodes were used in this experiment.

 

Exam Solutions

• Heating / cooking / lighting /named electrical appliance etc.
•  Magnetic effect, heating effect and chemical effect.
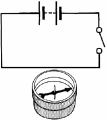• Connect a electrical calorimeter containing water to a power supply and notice the increase in temperature using a thermometer.
• Size of current, length of coil.
• Apparatus: see diagram

Procedure: close the switch
Observation: compass deflects

• High voltages result in smaller currents therefore less energy is lost as heat.
• Transfer the electrical energy at a higher voltage which would result in a lower current, therefore less energy lost as heat.
• P = I2R = (2002)(9.6) = 3.8 × 105 W
• P = V2/ R

40 = (230)2/ R
R = 1320 Ω

• Fuse, miniature circuit breaker, residual current device, earthing, 3 pin plug etc.
• Green and yellow
• Brown
• L (live) is brown, N (neutral) is blue, E (earth) is green-yellow
• The earth wire protects from electrocution / shock by conducting the current to earth.
• Live, brown
• Screw connections are fully tightened / fit the correct size fuse / ensure to match the colour codes
• It ‘blows’ and breaks the circuit if too large a current flows, preventing possible electrocution.
• When too high a current flows the thin wire heats up  and melts which breaks the circuit.
• The fuse blows which stops the current.
• It would allow too large a current to flow so the device could overheat.
• If a very large current flows the foil may still not break and so may start a fire.
• Copper
• I = P/V       Þ        I = 100/230

Range: 0.5 A fuse 

• P = VI        Þ I = P/V = 800/230 = 3.4 A

So the most suitable fuse is the 5 A fuse.

• P = VI        Þ I = P/V         Þ I = 2000/230 = 8.7 A
• The current is larger than the fuse rating, so the fuse will blow.
• They have a plastic housing so even if they are in contact with a live wire the current will not travel along the cover.
• It is an insulator.
• The metal parts are earthed.
• Bonding is where all metal pipes are connected to earth preventing accidental electrocution.
• Circuit breaker, trip switch, RCD, MCB
• It behaves as a fuse when too large a current flows 
• When the magnitude of the current flowing in is different from that flowing out.
• The RCD trips the circuit if the current reaches 30 mA.
• It acts as a safety device by breaking the circuit if there is a difference between the live and the neutral in a circuit.
• Miniature circuit breakers (MCBs) or residual current devices (RCDs).
• RCD responds v. Quickly, RCD responds to tiny currents
• Ions
• See graph
• If temperature was increasing it would no longer be linear; instead there would be a curve to the right because resistance would increase.
• Axes and straight line starting at v > 0
• The slope of the graph would be less (the resistance increases) due to less ions (charge carriers) being present.
• Axes, curve and plateau
• The kilo-watt hour is the amount of energy used by a 1000 Watt appliance in one hour.
• It records the amount of units used.
•  Number of kiloWatt hours = Number of kilowatts x Number of Hours = 2 × 3 =  6 kW hrs.

6 × 10 = 60 cent

 

•  
• Number of kiloWatt hours = Number of kilowatts × Number of Hours.

Power = 800 W = 0.8 kW
Time = 150 minutes = 2.5 hours
Number of kiloWatt hours   = 0.8 × 2.5 = 2 kWh

• Cost = 2 × 15 = 30 cent

 

•  
• See diagram below.
• Adjust the (variable) power supply // adjust the (variable) resistor

I/A	1.0	1.5	2.0	2.5	3.0	3.5	4.0
I 2/A2	1	2.25	4	6.25	9	12.25	16
Δθ/°C	2.2	5.0	8.8	13.8	20.0	26.0	35.2

•  

 

• 
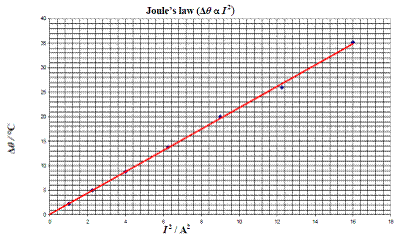
• See graph

 

 

 

 

 

 

 

 

 

 

 

 

• We got a straight line through the origin showing that Δθ α I2

•  
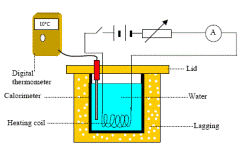• See diagram.
• The mass of water would be a third variable and you can only investigate the relationship between two variables at a time.
• Straight line graph through origin Þ Δθ α I2        Þ P α I2
• Electrical energy in = Heat energy out

RI2 t = mcΔθ
Rt = mc(Δθ/ I2)      Þ Rt = mc(slope)        Þ R = mc(slope)/t       = (.09)(4200)(3.8)/180
R = (7.8 ↔ 8.2) Ω

 

•  
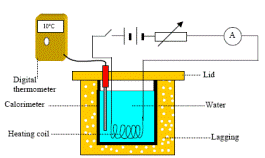
• See diagram.

I /A	1.5	2.0	2.5	3.0	3.5	4.0	4.5
Δθ / °C	3.5	7.0	10.8	15.0	21.2	27.5	33.0
I2 /A2	2.25	4.0	6.25	9.0	12.25	16.0	20.25

•  

 

Label axes
At least 6 correct points
Straight line
Good fit   
A straight line through origin shows that ∆ϑ    ∝    I2 which verifies Joule’s Law.

• You can only investigate the relationship between two variables at a time and time is a third variable.
• Start with cold water, change the water for each run, use a lid, shorter time interval, polish calorimeter.

 

• 
• An ammeter
• Using a voltmeter.
• Y is a rheostat which is a variable resistor; by adjusting it you vary the resistance which in turn varies the resistance and current.
•  See graph

 

 

• Take any two points and use the formula

 

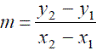
Slope = resistance = 1.67 Ω.

 

 

 

 

 

 

•  
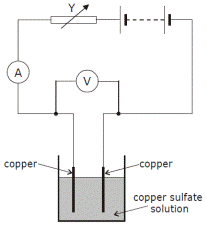
• See diagram. Cathode = negative electrode, anode = positive electrode
• Axes labelled

6 points plotted correctly
Straight line
Good fit

• Resistance = slope of graph = 19.5 to 20.5 Ohms
• Straight line starting at v > 0

 

 

 

 

Source : http://www.thephysicsteacher.ie/LC%20Physics/Student%20Notes/24.%20Effects%20of%20an%20Electric%20Current%20and%20Domestic%20Circuits.doc

Web site link: http://www.thephysicsteacher.ie

Author : not indicated on the source document of the above text

If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.

 

Effects of an electric current

 

 

Effects of an electric current

 

Main page

 

Alimentation - nutrition	Animals	Architecture	Art
Astrology, esoteric, parapsychology and fantasy	Astronomy	Biology and genetics	Botany and agriculture
Chemistry	Courses, training, guides, handbooks and tips	Culture General and actuality	Dermatology, health and wellness
Dictionaries and glossaries	Economics and finance	Education and pediatrics	Engineering and technology
English grammar and anthology	Fashion and show business	Fitness	Food, recipes and drink
Games, play space	Geography, geology and environment	History	Informatics and computer world
Jobs world	Languages	Leisure and DIY do it yourself	Lessons for students
Literature, biographies and journalism	Mathematics, geometry and statistical	Medicine	Music
Notes and concept maps	Philosophy	Photography and images - pictures	Physics
Physiology	Psychology and psychoanalysis	Quiz questions and answers	Religions
Rights law and political science	Science	Sociology and cultural anthropology	Sport
Summaries and reviews	Television, film - movies and comics	Theater and communications	Theses, themes and dissertations
Travel and tourist guides	Useful documents and tables	Utility, calculators and converters	Weather and meteorology

 

 

This is the right place where find the answers to your questions like :

Who ? What ? When ? Where ? Why ? Which ? How ? What does Effects of an electric current mean ? Which is the meaning of Effects of an electric current?

 

---

 

---

 

 

 

Alanpedia.com from 1998 year by year new sites and innovations

Main page - Disclaimer - Contact us