Types of energy
Types of energy
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Types of energy
Types of Energy
Mechanical Energy |
Wave Energy |
Kinetic Energy |
Kinetic Energy |
Potential Energy |
Potential Energy |
Rotational Energy |
|
Atomic/Nuclear Energy |
Solar Radiation |
Heat Energy |
Sound Waves |
Food Energy |
Water Waves |
Kinetic Energy = Energy of Motion
Potential Energy = Storage of Energy
Mechanical Energy
* The sum of the kinetic, potential, and rotational energies of a system.
ME = KE + PE + RE
*The mechanical energy does not include any internal energy associated with the structure of the system. It also excludes any thermal energy in the system.
|
* Energy due to an object's state of linear motion.
* The minimum Work needed to get an object of mass m moving at a speed v --starting from rest.
|
* Energy due to an object's state of rotational motion.
* The minimum Work needed to get an object with a moment of inertia I rotating at an angular velocity w - starting from rest.
Potential Energy
* The Work needed to change a system from one state of equilibrium to another state of equilibrium.
* Potential Energy is Stored Energy.
GRAVITY:![]()
Work needed to change an object's height relative to the Earth.
SPRING:![]()
Work needed to compress or stretch a spring.
PRESSURE:![]()
Work needed to change the volume of a Solid, Liquid, or Gas.
ATOMIC: ![]()
Work needed to split an atom up into its component parts.
Conservative Forces and Potential Energy
- Conservative Forces are reversible forces, meaning that the work done by a conservative force is recoverable, i.e. you can get out any work you put in or vise versa.
- When you apply an external agent to change the state of a system that is also acted upon by a conservative force then the system can be restored to its initial state without using any other external agent. Lifting a rock is one example.
- Each type of Conservative Force has an associated with it an Potential Energy. See table below.
- The Potential Energy is generally the equation for the work expressed in terms of the symbolic solution of the formula used to find the work. For example, Wgravity = PEgravity = m g h
- The work done by a conservative force, Wcf , can be transformed into a change in potential energy. We move the conservative Work term from one side of the work energy theorem to the other and associate it with the kinetic energy,
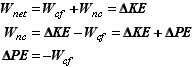
Examples: |
Conservative |
Potential |
Work |
Gravity |
F = m g |
PE = m g h |
DPE = m g (h2 - h1) |
Gravity |
|
|
|
Spring |
F = –k s |
|
|
Pressure |
F = P A |
PE = P V |
DPE = P (V2 - V1) |
Electrical |
|
|
|
- Conservative Forces are path independent, in that the work done by the force to move an object between any two points is independent of the path taken.
* The work done by a Nonconservative Force is not recoverable or expressible symbolically as a potential energy term. The work done by a nonconservitive force is usually dissipated as heat energy.
Examples: |
Non-Conseravtive |
Work- |
Friction |
f = µ n |
W = Ff d |
Human Push or Pull |
Fapp |
W = Fapp d |
Conservation of Energy For Conservative Forces:
- When the only forces acting on a system are conservative, the conservation of energy can be expressed as a conservation of the mechanical energy of the system.
![]()
or
![]()
Conservation of Energy for Nonconservative Forces:
- When a nonconservative force acts on a system, then its work contribution has to be added to (or subtracted from) the initial energy of the system in order to express the conservation of energy correctly.
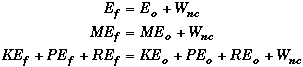
or
![]()
or

- When the system does nonconservative work then the Wnc term is negative, i.e. the system loses energy. The most common example of this is frictional loss.
Conservation of Energy Problem-Solving
The most general form of the Work-Energy Theorem is,
![]()
Reflective Mental Overseer Question:
To which system will I apply the conservation of work-energy?
* Select the system and consider the sources of any energy flow into or out of the system.
Is the system an isolated system ?
* An isolated system is one in which there is no energy exchange with its surroundings. If this is the case, then mechanical energy will be conserved.
![]()
* If the system is not isolated, then some energy (typically in the form of work) will flow into or out of the system. In this case you will have to use the generalized work-energy theorem to include the external force's work-energy contribution.
Will it be easier to solve the problem if I break the system up into two interacting subsystems ?
* You many have two or more systems exchanging energy with each other. One loses some energy while the other gains it.
![]()
What are the initial and final states of the system or systems ?
* Clarify in your mind the process described in the problem to determine the initial and final states of the system(s). A system's state includes both its spacial arrangement as well as its dynamic motion. For thermal problems this could include the initial and final temperature, pressure, or volume. For electrical problems this could include the initial and final amount of charge or voltage.
Are there any forces involved that do not have potential energy terms ?
* Determine which (if any) forces acting the system are non conservative forces. For nonconservative forces you will have to determine their energy contribution by calculating the work they do directly from the definition of work. If you cannot calculate the work directly, then you will probably have to use the above work-energy relation to find their work contribution.
What type of energies are involved in the process described in the problem ?
* Determine the energy contribution for any conservative forces by calculating the change in potential energy associated with that type of force between the initial and final states of the system.
Where will I locate the zero of potential energy ?
* To calculate potential energy, select an origin for the zero energy level associated with the potential energy. For gravity near the surface of the Earth this can be any vertical location. For a spring force this has to be the equilibrium position of the system.
Which energy terms can I calculate and which terms are unknown ?
* If possible, determine the initial and final kinetic energy of the system, and the initial and final potential energy of each type of conservative force acting on the system.
* Apply the generalized work-energy equation. Examine the resulting equation and solve for any unknowns. If you have more than one unknown, then you will need to look at the problem again to see if it states or implies any additional relationships between the unknowns (such as a geometrical association or a that the kinetic energy is constant).
Tarzan's Elevator
Tarzan finds a crashed cargo plane carrying a shipment of frictionless pulleys. He decides to build an elevator up to his tree house by installing a pair of these pullleys on a branch above his house. He runs a vine from a 25.0 kg platform which is resting on the ground, up through the two pulleys and down to a second identical platform hanging level with his tree house, 14.0 meters above the ground. On the second platform Tarzan has placed a counterweight equal to his own weight. To ride the elevator up to his tree house, he has Cheeta (his monkey companion) climb up the tree and jump onto the platform with the counterweight. (To ride from his house back down, Cheeta climbs up the tree again, and both Tarzan and Cheeta ride on the same, unwieghted platform.) Tarzan's mass is 105 kg, and Cheeta's mass is 46.0 kg. |
|
After Cheeta climbs onto the counterweighted platform, what is the mechanical energy of the elevator system (the two platforms and their loads) relative to the ground, when Tarzan and Cheeta pass each other ? |
|
What is the speed of Tarzan and Cheeta when they pass each other ? |
|
At what speed will Cheeta's platform hit the ground ? |
|
What is the height of Cheeta's platform when the mechanical energy of Tarzan's platform is the same as the mechanical energy of Cheeta's platform ? |
|
 Sketch and Process:
Sketch and Process:
One system (Cheeta's platform) is accelerated downwards by gravity, causing another less massive system (Tarzan's platform) to accelerate upwards due to its connection to the first system via a vine-rope over a pair of frictionless pulleys.
Givens and Labels:
Tarzan's Platform |
Cheeta's Platform |
||
|
|||
mT |
= 25.0 kg + 105 kg = 130 kg |
mC |
= 130 kg + 46.0 kg = 176 kg |
The total mass of each subsystem. |
|||
|
|||
vTo |
= 0 |
vCo |
= 0 |
The velocities of the platforms when the elevator is set into motion, the initial velocities. |
|||
|
|||
vTf |
= ? |
vCf |
= ? |
The platform velocities when Tarzan reaches the tree house, the final velocities. |
|||
|
|||
yTo |
= 0 |
yCo |
= ho = 14.0 m |
Height of tree house above the ground, the initial position of the platforms. |
|||
Relevant Physics:
It is assumed that the vine does not stretch. In particular, this implies that the velocity and the acceleration of both platforms are always the same at any instant in time. As a result we only need to use one symbol to specify either the velocity or the acceleration. Mathematically,
vC = vT = v
aC= aT = a
This assumption also implies something about the heights of the two platforms at any moment. Namely, the constraint
yC = ho - yT
yT+ yC = ho
For each centimeter Cheeta descends, Tarzan will rise one centimeter.
The other (and main) principle needed to analyze this problem is the conservation of energy. We choose both platforms to be our system, with each platform being a subsystem. Since the pulleys are assumed to be frictionless, the big-system is isolated and the total mechanical energy of the elevator system is always the same throughout the motion of the two platforms (until after Cheeta's platform hits the ground).

At this point we could also substitute yC= ho- yT into the above equation to reduce the number of unknowns even further, but we will leave that until later in the solution.
It useful to observe that the conservation of energy also means that any energy gained by one platform is lost by the other platform.
A) Find the ME when the platforms pass.
Using the subscript "p" to denote the location when they pass, the total mechanical energy at this point will be equal to
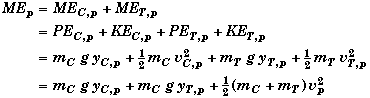
Recall that the velocities of the two platforms are equal because the vine-rope is assumed not to stretch.
We could calculate the MEp if we knew the height of the platforms when they pass and their velocity. We do know their height, ho/2, but we do not know their speed. However, we do not need to know either of these variables to determine the MEp since energy is conserved. We only need to determine the ME at some point where we do know the heights and the speed. In this case, we know these two values at the start of the problem,
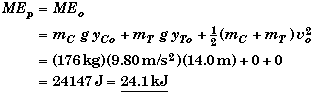
Note that this is the total mechanical energy for any location of the platforms.
(B) Find the velocity vp when the platforms pass.
When the two platforms pass each other, yCp = yTp = ho/2, and the mechanical energy of the elevator system is still equal to its initial mechanical energy.
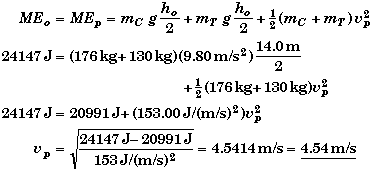
(C) Find the velocity vf when Cheeta's platform hits the ground.
Here yCf = 0 and yTf = hoand energy is still conserved at the moment Cheeta's platform just touches the ground.
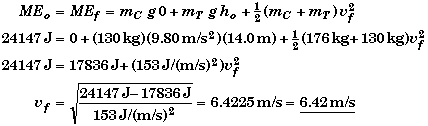
Symbolic Solution to (B) & (C)
Using the constraint yC = ho- yT in the conservation of energy equation,

This equation gives the velocity at any height of the platform which Tarzan is riding.
For B at yT = ho/2
![]()
For C at yT = ho
![]()
In a real-world situation where there is friction, the velocity of the platforms would level out at a constant value when the energy loss due to friction equaled the energy input due to gravity. This terminal velocity would occur when the net force on the system equaled zero.
D) Find yC when the platforms' mechanical energies are equal.
Turning this into a mathematical statement, it means find yC when
MEC = MET
In addition, energy is conserved so that
MEo = MEC + MET
Together these two equations imply
![]()
In terms of heights and speed these become
![]()
This gives us two equations with three unknowns: yC, yT, & v. At this point one could solve this problem as three simultaneous equations with three unknowns,
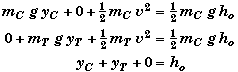
or
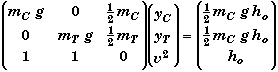
A more direct method is to first eliminate v by subtracting the two energy equations and then substitute yT = ho- yC for yT. Before we do, let us simplify the two equations,
![]()
by dividing out the masses and multiplying by 2.
![]()
Subtracting,
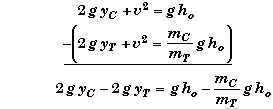
Substituting yT = ho - yC, we get
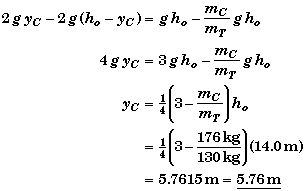
This solution also implies that unless the mass of Tarzan's platform is less than three times that of Cheeta's platform, then the mechanical energies of the two platforms can never be equal before Cheeta hits the ground.
Using this expression for yC, we can put it back into one of the energy equations and solve for the velocity when their two mechanical energies are equal. Although not requested, the result is
![]()
Jumping Flea Problem
A 450 microgram flea is observed to jump to a height of 3.50 cm. When the flea's legs have extended .500 mm above the surface, the flea is observed to be moving at a speed of approximately 1.00 m/s. |
|
(A) |
What is the average force exerted by the flea's legs during its jump ? |
(B) |
What is the average power output of the flea's legs during its jump ? |
(C) |
What is the energy loss due to air resistance during the first half of the flea's jump on its way up ? |
(D) |
If the energy loss due to air resistance on the flea's way down is the approximately the same as on its way up, how fast will the flea hit the ground ? |
Sketch and Process:
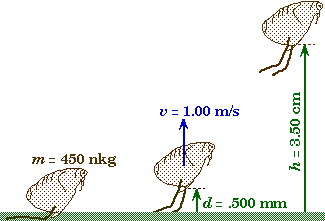
A flea extends his legs to exert a force that propels the flea into the air.
Givens and Labels
m |
= 450x10-9 kg |
(Mass of the flea.) |
d |
= 5.00x10-4 m |
(Length of flea's legs.) |
h |
= .0350 m |
(Maximum height attained by the flea.) |
vj |
= 1.00 m/s |
(Flea's velocity immediately after take off.) |
Relevant Physics:
This problem can be analyzed by looking at the work-energy flow.
The work done by the flea's legs goes into the flea's mechanical energy at take off.
![]()
Since the flea's legs are 0.500 mm long, we can assume that this is the distance over which the flea applies a force to launch itself.
![]()
Since this problem requests the power output of the flea during its jump, we will need to find the time it takes for the flea to launch itself. The conservation of energy cannot be used to find the time, so we will have to assume the acceleration of the flea is constant so that we can find the time knowing the distance and the final velocity.
The maximum height that the flea jumps is less than the maximum height attainable when there is no air resistance. This can be analyzed by using the conservation of energy. Any energy lost must be equal to the energy difference between the ideal no-energy-loss case and the actual energy observed.
(A) Find the average force exerted by the flea's legs, Flegs.
From the work-energy theorem,
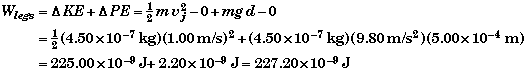
From the definition of work,
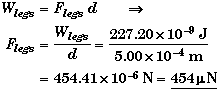
(B) Find the average power exerted by the flea's legs during its take off, Pave.
The average power is determined from
![]()
To determine the time required for take off, we can use Newton's 2nd Law to find the flea's average acceleration.
![]()
We can now estimate the time required for the flea to take off.
![]()
Finally,
![]()
(C) Find the energy loss during the first half of the flea's flight, Eloss.
First let us calculate how high the flea could have jumped if there were no air drag on the flea. Using the conservation of energy,
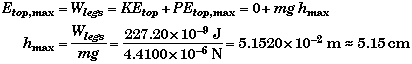
The energy loss is equal to the maximum energy minus the actual energy at the top,
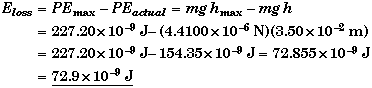
The fractional energy loss is given by
![]()
(D) Assuming the same energy loss on the way up and on the way down, find the velocity of the flea when it lands.
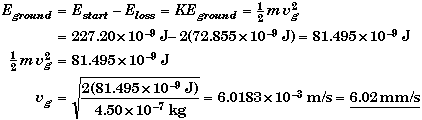
It would seem more reasonable to assume the same fractional energy loss on the way down as up, rather than assuming the same total amount. One would not expect as much energy loss on the way down as up, because the flea's speed is going to be smaller, as a whole, on the way down.
The starting energy at the top of the flea's trajectory is
![]()
If the flea lost 32.065% of this energy on the way down then final energy would be (1-.32065)(154.35 J) = 104.86 J. For this energy, the flea's speed when it lands would be
![]()
Source : http://physics.mtsac.edu/4A/4A%20Text/TypesofEnergy.doc
Web site link: http://physics.mtsac.edu/
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Types of energy
Types of energy
Types of energy
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Types of energy mean ? Which is the meaning of Types of energy?
Types of energy physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us