Force
Force
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Force
Syllabus
OP4 Appreciate the concept of force, recall that the newton is the unit of force, and describe forces and their effects
OP5 Investigate examples of friction and the effect of lubrication
OP6 Investigate the relationship between the extension of a spring and the applied force
OP7 Recall that weight is the force of gravity and that weight can vary with location; recall that mass in kilograms multiplied by 10 is approximately equal in magnitude to weight in newtons on the surface of the earth.
Student Notes
A force is something that causes an object to change velocity or accelerate.
The newton (symbol N) is the unit of force.
Forces can be measured using a spring-balance (the proper name is a newton-meter).
Friction
Friction is a force that opposes motion between two objects in contact.
Friction can be a nuisance (e.g. it slows things down when you don’t want it to when driving a car or riding a bike).
Friction can also be useful (e.g. brakes on a bike, and to enable us to walk).
Experiment: To demonstrate friction and how a lubricant can be used to reduced friction.
Attach a spring balance to a wooden block and use it to pull the block over the bench. Note the reading on the spring-balance.
Now put some oil or grease under the block and repeat. Notice that the force required to pull the block is much less.
Weight and Mass
Mass is a measure of the amount of matter (“stuff”) in something.
The weight of an object is a measure of the gravitational pull on it.
Weight is a force (due to gravity)
The mass of an object doesn’t change from one place to the next because it still has the name amount of stuff inside (the same number of atoms), but the weight of the object will be much less on a planet smaller than Earth (or on the moon) while it will weigh much more (it will be much ‘heavier’) on a bigger planet. In fact if you could go to one of the bigger planets you would not even be able to stand up because you weigh so much!
Maths Problems
Weight (in newtons) = Mass (in kilograms) × 10
e.g. a student of mass 60 kg has a weight of 600 N.
Note: There are 1000 grams in a kilogram (kg).
Hooke’s Law
The extension of a stretched string is directly proportional to the force that is stretching it
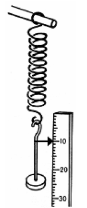
This means that if the force on the string doubles so will the extension; if the force triples then the extension will also triple, etc.
Experiment: To investigate the relationship between the extension of a spring and the force that is stretching it.
- Use a newton-meter to stretch a spring and note the extension and the force used.
- Repeat for lot of different forces.
- Plot a graph of force used against extension.
- Result: You should get the graph on a straight line.
- Conclusion: The graph is a straight line through the origin which shows that the extension is directly proportional to the applied force.
{Strictly speaking stating Hooke’s Law is not on the syllabus but it did get asked by mistake one year so it’s best to learn it just in case it happens again. You do however have to know the experiment.}
Exam questions
- [2007 OL]
Metre |
Newton |
Joule |
Different units are used to measure different physical quantities.
- Pick the unit of length from the table on the right.
- Pick the unit of weight from the table on the right.
- [2009 OL]
Friction can be useful when driving a car.
- Name one way in which friction is useful when driving a car.
- Name one possible way to reduce friction.
- [2006 OL]
Friction is an example of a force.
- Give another example of a force.
- Give one way to reduce friction.
- After what scientist is the unit of force named?
- [2008]
Give two effectsthat gravity has on your everyday life.
- [2009]
- A stone was dropped from the top of a tall cliff. Name the force that causes the stone to fall downwards.
- The stone had a mass of 2 kg. What was the weight of the stone on earth? Give the unit.
- [2006]
Distinguish between weight and mass.
- [2006]
State Hooke’s law.
{This isn’t on the syllabus and shouldn’t have got asked, so presumably won’t appear again – but you never know}Robert Hooke (1635-1703) made a number of discoveries including the effect of force on elastic bodies now known as Hooke’s law.
- [2009 OL]
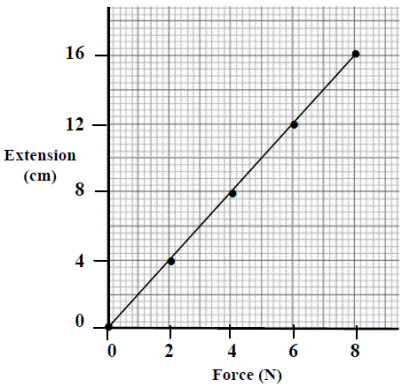A student investigated the relationship between the extension of a spring and the force applied to it.
The equipment shown in the diagram was used.
The data collected is shown in the table.
Force (N) |
0 |
2 |
4 |
6 |
8 |
Extension (cm) |
0 |
4 |
8 |
12 |
16 |
The student then drew the graph shown.
Answer the questions that follow about this investigation.
- Name an instrument used to measure the force in this investigation.
- Describe how the student could have measured the extension of the spring.
- What conclusion would you draw from this investigation?
- [2006 OL]
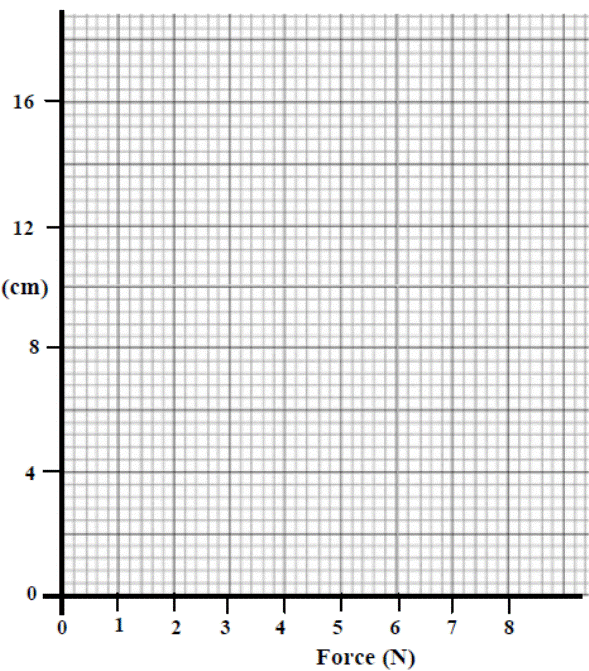
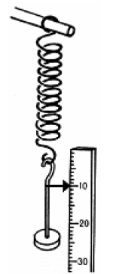A student carried out an investigation to examine the relationship between the extension (increase in length) of a spring and the force applied to it.
The diagram shows the apparatus used.
The table shows the data collected by the student.
Force (N) |
0 |
2 |
4 |
6 |
8 |
Extension (cm) |
0 |
4 |
8 |
12 |
16 |
- Describe how the student could have taken any one of these measurements.
- Draw a graph of the extension (y-axis) against the force in the grid provided on the right.
- What force results in a 6 cm extension of the spring?
- [2006]
A student was given a box of identical springs and asked to analyse them so that they could be used as newton meters. The student performed an experiment, using the apparatus shown in the diagram, on one of the springs.
In the experiment the student measured the increase in length of the spring caused by a number of weights. The spring was tested to destruction (that is weights were added until the spring was damaged).
The data from the experiment is given in the table.
Weight (N) |
0.0 |
0.4 |
0.8 |
1.2 |
1.6 |
2.0 |
2.4 |
Extension (cm) |
0.0 |
2.0 |
4.0 |
6.0 |
8.0 |
8.5 |
8.6 |
- Plot a graph of extension (increase in length – y-axis) against weight (x-axis)in the grid provided.
- Use the graph to find the weight that would produce an extension of 5 cm in the spring.
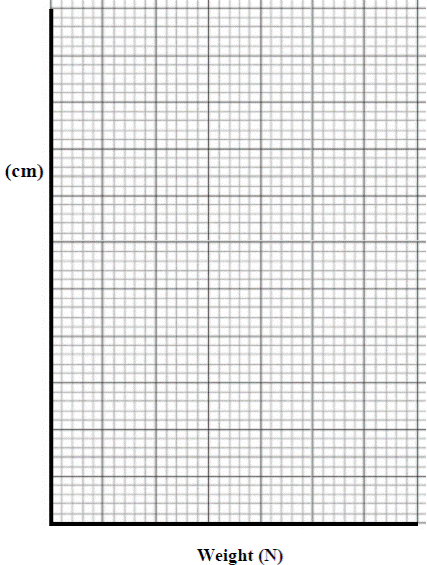
- Study your graph carefully.
The spring obeys Hooke’s law for the earlier extensions and then when the spring becomes damaged it does not appear to do so.
Estimate, from your graph, the weight after the addition of which the law seems no longer to apply.
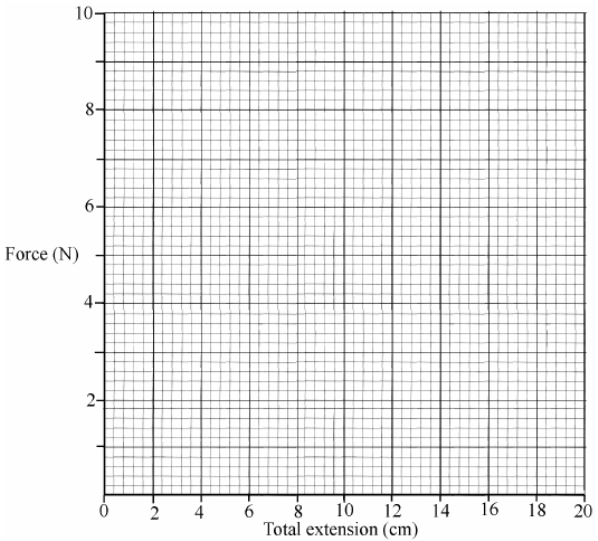
- [2010]
A pupil used the apparatus shown in the diagram to investigate the relationship between the force applied and the extension produced in the spring by that force.
Pointer, P, was used to read the scale.
Weights were added to the pan to apply forces to the spring.
The data recorded is in the table.
Force |
Scale reading |
Total extension |
0 |
31.0 |
|
2 |
35.0 |
|
4 |
39.0 |
|
6 |
43.0 |
|
8 |
47.0 |
|
10 |
51.0 |
|
- Calculate the total extension for each force and enter them in the table.
- Draw a graph of force against total extension in the grid below.
- What conclusion can be drawn from the graph regarding the relationship between the force applied to the spring and the extension produced by it?
- Use the graph to determine the weight of a stone that produced an extension of 14 cm in the spring.
Exam Solutions
- Metre
- Newton
- Grip / traction / road holding / stopping
- Oiling / waxing / greasing / polishing / lubricants / bearings
- Gravity / weight / push / pull / magnetic / electric / twist
- Oiling / lubrication / wax / polish / ball bearings
- Newton
- It gives things weight/ it keeps things on the surface of the earth/ it causes things to fall…
- Gravity
- Weight = mass × 10 = 2 × 10 = 20 N (Newtons)
- Weight is a force which is caused by gravitational pull.
Mass is a measure of the amount of matter in something.
- The extension of a stretched string depends on the force applied to it.
- Add (hang) weights onto the string and measure the extension using the metre stick
- Plot all the points and draw a straight line.
- 3 N
- Spring balance / Newton meter
- By using a ruler or a metre stick
- The extension is directly proportional to force applied / as force is increased the extension increases at the same rate.
- See graph
- Weight = 1.0 N (accept range 0.9 to 1.1)
- 1.6 N (accept range 1.6 to 2.0)
Force |
Scale reading |
Total extension |
0 |
31.0 |
0 |
2 |
35.0 |
4 |
4 |
39.0 |
8 |
6 |
43.0 |
12 |
8 |
47.0 |
16 |
10 |
51.0 |
20 |
- See table
- See graph
- The extension is directlyproportional to applied force (you must use the word directly)
- 7 N
Other Test Questions
- What is meant by the term ‘force’?
- What is meant by the term ‘friction’?
- Give an example of how friction can be useful on a bicycle?
- Give an example of how friction can be a nuisance on a bicycle?
- How might a cyclist reduce friction?
- Give another example of how friction can be useful.
- Give another example of how friction can be a nuisance.
- Describe how you would investigate the effectiveness of two different lubricants.
Include reference to a control.
Give three ways of making sure that you carry out a fair test.
- Name two instruments used to measure weight.
- Calculate the weight (in Newtons) of a bag of sugar, which has a mass of 5 kg.
- A man has a mass of 100 kg. What is his weight?
- Would the man weigh less or more on the moon?
- Why does the man have a different weight on the moon?
- What will be the mass of the man on the moon?
- How would you be affected if your weight suddenly doubled?
Source : http://www.thephysicsteacher.ie/JC%20Science/JC%20Physics/Student%20Notes/4.%20Force.doc
Web site link: http://www.thephysicsteacher.ie
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Force
Force
Force
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Force mean ? Which is the meaning of Force?
Force physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us