• 

 

Force mass and momentum

 

 

---

 

Force mass and momentum

 

The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.

We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge

Physics

 

Force mass and momentum

 

A Force is anything which can cause an object to accelerate.
The unit of force is the Newton (N)*.

A force of 1 N gives a mass of 1 kg an acceleration of 1 m s-1.

The Mass of an object is a measure of how difficult it is to accelerate that object.
Or
The Mass of an object is a measure of its Inertia.
(The inertia of an object in turn is a measure of how difficult it is to accelerate it.)

The unit of mass is the kilogram (kg).

Relationship between Force, Mass and Acceleration

  

                      
Always remember:  “AN UNBALANCED FORCE PRODUCES AN ACCELERATION”

 

Weight

The weight of an object is a measure of the force of the Earth’s gravity acting on it.

 

 

Because weight is a force, it follows that the unit of weight is also the Newton.
See problems 2 – 6, page 93. Then try Exercise 9.1, questions 1 – 10, page 93.

 

Friction
Friction is a force which opposes the relative motion between two objects.
Examples of Friction: Brakes, Walking, Air Resistance

 

Look at Worked Problems 8 and 9, page 97. Then try questions 1 – 5, page 97.

 

Momentum

 

 

The symbol of momentum is r; pronounced “row”)
The unit of Momentum is the kilogram metre per second (kg m s-1)

 

Newton’s Laws of Motion

 

Applications of Newton’s laws of motion: Seat belts / Rocket travel / Ball games

To Show that F = ma is a special case of Newton’s Second Law

From Newton II: Force is proportional to the rate of change of momentum
Force µ rate of change of momentum
F µ (mv – mu)/t
F µ m(v-u)/t
F µ ma
F = k (ma)
F = ma

Note: k = 1 because of how we define the newton (a force of 1 N gives a mass of 1 kg an acceleration of 1 m s-2)*

 

The Principle of Conservation of Momentum
states that in any collision between two objects, the total momentum before impact equals total momentum after impact, provided no external forces act on the system.
(If you forget the bit in italics you lose half marks!)

 

  

In symbols                                         

 Note that if the two objects coalesce (stick together) after collision,
there is only one final velocity, and the above equation becomes

See problems 10 – 13, page 97, 98. Then try questions 1 – 10, Exercise 9.3, page 100.

 

Areas where the principle of conservation of momentum applies:

• Collisions (ball games)
• Acceleration of aircraft
• Jet aircraft

 

Mandatory Experiments

• To show that the acceleration of a body is proportional to the force acting on it. Page 91
• To Verify the Principle of Conservation of Momentum. Page 101

 

 Leaving Cert Physics Syllabus

Content	Depth of Treatment	Activities	STS
1.Newton’s laws of motion	Statement of the three laws.	Demonstration of the three laws using air track or tickertape timer etc.	Applications: seat belts rocket travel. Sports, all ball games.
	Force and momentum: definitions and units. Vector nature of forces to be stressed. F = ma as a special case of Newton’s second law. Friction: a force opposing motion.	Appropriate calculations.	Important of friction in everyday experience, e.g. walking, use of lubricants etc.
2. Conservation of momentum	Principle of conservation of momentum.	Demonstration by any one suitable method. Appropriate calculations.	Collisions (ball games), acceleration of spacecraft, jet aircraft.

 

TO SHOW THAT ACCELERATION IS PROPORTIONAL TO THE FORCE WHICH CAUSED IT

APPARATUS
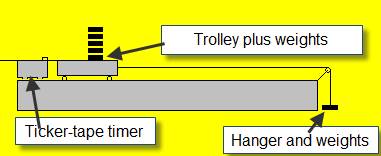
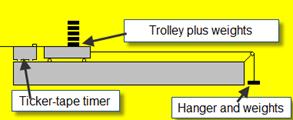
Set of weights, electronic balance, trolley, ticker-tape timer and tape.

DIAGRAM

PROCEDURE

• Set up the apparatus as shown in the diagram.

• Start by taking one weight from the trolley and adding it to the hanger at the other end.

 

• Note the weight at this end (including the weight of the hanger) using an electronic balance.

• Release the system which allows the trolley to accelerate down the track.

 

• Use the ticker-tape timer to calculate the acceleration.

• Repeat these steps about seven times, each time taking a weight from the trolley and adding it to the other end.

 

• Record the results for force and acceleration in a table.

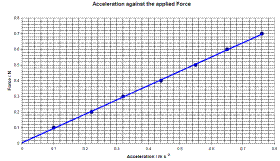
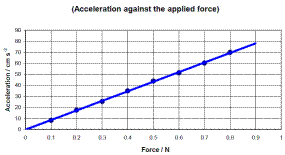
• Draw a graph of Force (on the y-axis) against acceleration (on the x-axis).  The slope of the graph corresponds to the mass of the system (trolley plus hanger plus all the weights)

 

RESULLTS

Force (N)	Acceleration (m s-2)

CONCLUSION
Our graph resulted in a straight line through the origin, verifying that the acceleration is proportional to the force, as the theory predicted.
The slope of our force-acceleration graph was 0.32, which was in rough agreement with the mass of the system which we measured to be 0.35 kg.

 

PRECAUTIONS / SOURCES OF ERROR

• When adding weights to the hanging masses, you must take them from on top of the trolley.

• Ensure that the runway in smooth, free of dust, and does not sag in the middle.

 

• Ensure that the runway is tilted just enough for the trolley to roll at constant speed when no force is applied.

 

When must the hanging weights be taken from on top of the trolley?
Answer: so that the mass of the system can be kept constant

 

 

 

 

 

 

 

 

 

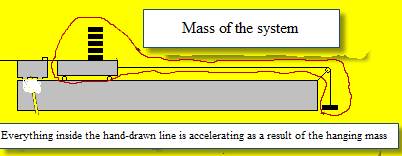
We’re looking to investigate the relationship between the acceleration of an object and the force which caused it.
The force which is causing the acceleration is the hanging weights. What mass is accelerating as a result of these weights dropping?
Well obviously the trolley plus the weights sitting on it are accelerating, but not just that; the hanging weights themselves are also accelerating, so the total mass accelerating as a result of the hanging weights is:
trolley + weights sitting on trolley + hanging weights
Now if we’re looking to investigate the relationship between the acceleration of an object and the force which caused it we need to keep all other variables constant. In this case one other variable is the mass which is )being accelerated. The only way to increase the hanging weights while keeping the mass of the system constant, is to transfer weights from the trolley to the hanging weights.

 

 

Using the ticker-tape system

If using the ticker-tape you will need to calculate the velocity at the beginning (u = s1/ t1), the velocity at the end (v = s2/ t2) and then use the equation v2 = u2 + 2as, where s is the distance between the middle of first set of dots and the middle of the second set of dots.

s1 (m)	t1(s)	u (m s -1)	s2 (m)	t2(s)	v (m s -1)	s (m)	a (m s-2)	Force (N)

 

We pretended that we were using the ticker-tape system, in which case we would need to fill in a table like the one above just to work out the acceleration each time. Because we used a datalogger we didn’t need to do this.
The computer told us what the acceleration was for each run, which made the experiment a lot cleaner and easier to follow.

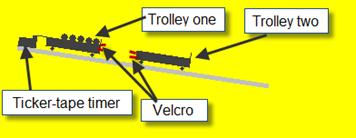
TO VERIFY THE PRINCIPLE OF CONSERVATION OF MOMENTUM

APPARATUS
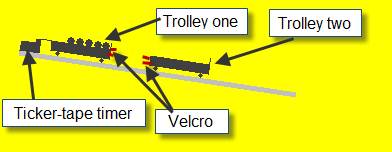
Set of weights, electronic balance, trolley, ticker-tape timer and tape.

DIAGRAM

PROCEDURE

• Set up the apparatus as shown in the diagram. The track is tilted slightly so that the trolleys will move at constant velocity when given an initial push.

 

• Note the mass of both trolleys to begin with.

• Both trolleys are initially at rest.

 

• Trolley one is given an initial push such that it moves at constant velocity until it collides with Trolley two whereupon they will join together (because of the velcro) and move off as one combined mass

• Use the ticker-tape to calculate the velocity of Trolley one before the collision and the velocity of the combined mass after the collision.

 

• Repeat the experiment a few times, each time adding masses from one trolley to the other .

• Record the results in the table and for each run calculate the total momentum before and after the collision.

 

RESULTS AND CALCULATIONS:

 

CONCLUSION
After completing the experiment we found that in each case the total momentum before the collision equalled the total momentum after the collision  (within the limits of experimental error), in agreement with the theory.

 

SOURCES OF ERROR / PRECAUTIONS

• Ensure that the runway in smooth, free of dust, and does not sag in the middle.

• Ensure that the runway is tilted just enough for the trolley to roll at constant speed.

Notes

If using the linear air-track

• In this case friction isn’t an issue and therefore the air-tack should be level.

To see if the track is level check that the trolley doesn’t drift toward either end.

• Block the ten pairs of air holes nearest the buffer end of the track with cellotape. This part of the track will now act as a brake on the vehicle.
• Occasionally check the air holes on the linear air-track with a pin, to clear any blockages due to grit or dust.

 

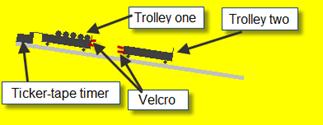
If using the traditional ramp and ticker-tape timer

• The track is tilted slightly (as in the diagram above) so that the trolleys will move at constant velocity when given an initial push.
• Ignore the first few dots on the tape. These represent where the trolley was being pushed.

 

Data-loggers
We use data-loggers to calculate the velocities because it’s much easier than counting dots on a piece of tape or working out horrendous amounts of calculations associated with the light-gates and air-track. However since the examiners expect old-fashioned answers, we will pretend that we used the ticker-tape.

 

Sample results using the data-logger

MOMENTUM BEFORE							MOMENTUM AFTER
				Total Before					Total After
m1	u1	m1u1	m2u2	m1u1+m2u2		m2	(m1 + m2)	v3	(m1 + m2)v3
.25	.36	.09	0	.09		.25	.5	.17	.09
.5	.41	.205	0	.21		.25	.75	.26	.20
.5	.55	.275	0	.28		.5	1.0	.28	.28
.75	.45	.34	0	.34		.25	1.0	.34	.34

 

Extra Credit
Odd as it may seem, most people’s views about motion are part of a system of physics that was proposed more than 2,000 years ago and was experimentally shown to be inadequate at least 1,400 years ago.
I. Bernard Cohen

*Isaac Newton
Something most textbooks are uncomfortable with is the fact that the great Isaac Newton spent over 90 per cent of his time obsessing about alchemy, biblical prophecies and religious disputations, all of which were complete tosh.
The other ten per cent merely changed our view of both science and the universe.
It wouldn’t be too great an exaggeration to say that his scientific research was almost an afterthought.
One noted historian claimed that Newton was not the first great scientist; he was the last of the great mystics.
It seems that Newton died a virgin, and never had so much as a romantic attachment, though he lived to be 84.

*Newton’s Third Law of Motion
Some other examples:
A balloon flying around the room while deflating.
The movement of a garden hose when it is lying on the ground spraying out water.
The recoil of a rifle could easily shatter a man’s shoulder if not held properly.
The first cannon-ships actually capsized due to the recoil of all the cannons being fired at the same time. Subsequent ships had to be redesigned.

These are also examples of Conservation of Momentum
Before the rifle was fired there was no momentum. After the rifle was fired there was the momentum of the bullet going forward (small mass by high velocity) which equalled the momentum of the rifle going backwards (big mass by small velocity). Because they were moving in opposite directions one was positive while the other was negative so their total was again zero.
The same analysis applies to a rocket ship in space firing gas to move. In this case the small mass is the gas going in the opposite direction to the ship. This occasionally gets asked in exams.

Newton’s Third Law leads to some unusual consequences
If you push against a wall with a force of 20 Newtons, the wall pushes back against you. Seems odd?
Well, think about your book which sits on the table. There is a force pulling it downwards, and yet it doesn’t fall through the table – why not?
There must be an equal and opposite force acting upwards to cause the book to remain at rest. But where can this force come from?
It’s actually the electrons of the atoms on the wall repelling the electrons in the atoms of your book. If you could look at the two surfaces very closely, you would actually see a ‘mesh’ of electrons repelling each other, and the respective surfaces deforming slightly.

While we’re at it may be a good time to also consider the following; An atom is 99.99999% empty space.
Which basically means we are little more than walking, talking, thinking holograms!
So why does my book, and you, and me (which are all just made up of atoms after all) feel solid?
And for that matter why does it look solid?
Now can you explain how a wall can push back at a force equal to that which you are applying?
So if the wall does push back, why don’t you accelerate backwards?

*k = 1 because of how we define the various units: a force of 1 N gives a mass of 1 kg an acceleration of 1 m s-2
This is also key to why we are stuck with the kilogram as the basic unit of mass. If we are defining the Newton and the m s-2 as the basic units of force and acceleration respectively then F = ma tells us that the m must be the basic unit of mass, which in this case is the kilogram. Now I suppose we could re-name this particular amount of matter and call it one gram (and the kilogram would be another name for a tonne), and if we were starting out again I suppose that’s what we would do, but we’re not starting from scratch and it would just be too confusing to change things at this stage.

Moment and Momentum:  Origin of Terms
Contraction of *movimentum, from movere "to move."
Notion of a particle so small it would just "move" the pointer of a scale led to sense of time division, which gave rise to the term moment of time.

Still, why p for momentum?
Well, Newton thought of "moments" in a more mathematical, abstract sense in the calculus he was inventing (moments of inertia, for example).
In the scientific community at the time Newton published the Principia, *impetus* was the quality of an object that was moving independent of an observed force.
Furthermore, the equation p=mv wasn't given first by Newton, but was developed afterwards.
P was a convenient symbol - m would be confused with mass, i is too often used to indicate an instance of an object. (Mi usually means the mass of the  ith object.)Conservation Laws - Angular Momentum

Fun Activity
Get a couple of students to hold up a large sheet (an old bed-sheet will do fine) and get others to throw eggs at it (one at a time) as hard as they can.
The eggs will never break because the sheet deforms on impact, increasing the impact time. Therefore the rate of change of change of momentum is less, resulting in a reduced force acting on the egg (from Newton’s Second Law above).

This has some serious real-world applications.
All cars have built-in ‘crumple-zones’ which are deliberate weak links in the structure of the car. If the car crashes these sections crumple taking valuable fractions of a second to do, again decreasing the rate of change of momentum. So while the car looks worse as a result of this modification, your chances of surviving actually increase.
Google videos of car crashes and car crash tests for more, or as a class activity build your own crumple zones on the front of a trolley to try and stop a nail impaling a plasticine man.

Why diet? Visit the moon and lose weight!

Physics  Exam questions

 

• [2004][2006 OL][2008 OL]

Define force.

• [2008]

Define the newton, the unit of force.

• [2002 OL]

Copy and complete the following statement of Newton’s first law of motion.
“An object stays at rest or moves with constant velocity _______________________________”.

• [2010]

A spacecraft carrying astronauts is on a straight line flight from the earth to the moon and after a while its engines are turned off.
Explain why the spacecraft continues on its journey to the moon, even though the engines are turned off.

• [2002][2003][2004][2007 OL]

State Newton’s second law of motion.

• [2006]

State Newton’s third law of motion.

• [2009]

State Newton’s laws of motion.

• [2004 OL]

The cheetah is one of the fastest land animals. Calculate the resultant force acting on the cheetah while it is accelerating at a rate of 7 m s-2. The mass of the cheetah is 150 kg.

• [2004 OL]

Name two forces acting on a cheetah while it is running.

• [2003 OL][2006 OL]

An astronaut of mass 120 kg is on the surface of the moon, where the acceleration due to gravity is 1.6 m s–2. What is the weight of the astronaut on the surface of the moon?

• [2006 OL]

Why is the astronaut’s weight greater on earth than on the moon?

• [2006 OL]

The earth is surrounded by a layer of air, called its atmosphere. Explain why the moon does not have an atmosphere.

• [2008 OL]

A lunar buggy designed to travel on the surface of the moon (where acceleration due to gravity is1.6 m s-2) had a mass of 2000 kg when built on the earth.

• What is the weight of the buggy on earth?
• What is the mass of the buggy on the moon?
• What is the weight of the buggy on the moon?
• A powerful rocket is required to leave the surface of the earth.

A less powerful rocket is required to leave the surface of the moon. Explain why.

• [2002 OL]

The diagram shows the forces acting on an aircraft travelling horizontally at a constant speed through the air.
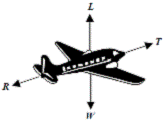L is the upward force acting on the aircraft. W is the weight of the aircraft.
T is the force due to the engines. R is the force due to air resistance.

• What happens to the aircraft when the force L is greater than the weight of the aircraft?
• What happens to the aircraft when the force T is greater than the force R?
• The aircraft was travelling at a speed of 60 m s-1 when it landed on the runway. It took two minutes to stop. Calculate the acceleration of the aircraft while coming to a stop.
• The aircraft had a mass of 50 000 kg. What was the force required to stop the aircraft?
• Using Newton’s first law of motion, explain what would happen to the passengers if they were not wearing seatbelts while the aircraft was landing. 

 

• [2006]

Draw a diagram to show the forces acting on the ball when it is at position A.

• [2003]

If the mass of a skydiver is 90 kg and his average vertical acceleration is 0.83 m s-2, calculate the magnitude and direction of the average resultant force acting on him?

• [2003]

Use a diagram to show the forces acting on the skydiver and explain why he reaches a constant speed.

• [2004]

A block of mass 8.0 g moved 2.0 m along a bench at an initial velocity of 2.48 m s-1 before stopping.
What was the average horizontal force exerted on the block while travelling this distance?

 

 

 

 

• [2009]

A skateboarder with a total mass of 70 kg starts from rest at the top of a ramp and accelerates down it. The ramp is 25 m long and is at an angle of 200 to the horizontal. The skateboarder has a velocity of 12.2 m s–1 at the bottom of the ramp.

• Calculate the average acceleration of the skateboarder on the ramp.
• Calculate the component of the skateboarder’s weight that is parallel to the ramp.
• Calculate the force of friction acting on the skateboarder on the ramp.
• What is the maximum height that the skateboarder can reach? (acceleration due to gravity = 9.8 m s–2)
• Sketch a velocity-time graph to illustrate his motion.

• [2003]

A person in a wheelchair is moving up a ramp at a constant speed. Their total weight is 900 N.
The ramp makes an angle of 10o with the horizontal.
Calculate the force required to keep the wheelchair moving at a constant speed up the ramp. (You may ignore the effects of friction.)

• [2007][2002 OL][2006 OL][2009 OL]

What is friction?

 

 

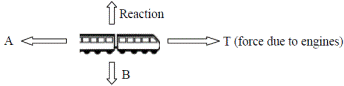• [2009 OL]

The diagram shows the forces acting on a train which was travelling horizontally.
A train of mass 30000 kg started from a station and accelerated at 0.5 m s−2 to reach its top speed of 50 m s−1 and maintained this speed for 90 minutes.
As the train approached the next station the driver applied the brakes uniformly to bring the train to a stop in a distance of 500 m.

• Calculate how long it took the train to reach its top speed.
• Calculate how far it travelled at its top speed.
• Calculate the acceleration experienced by the train when the brakes were applied.
• What was the force acting on the train when the brakes were applied?
• Name the force A and the force B acting on the train, as shown in the diagram.
• Describe the motion of the train when the force A is equal to the force T.
• Sketch a velocity-time graph of the train’s journey.

(v = u + at , v2 = u2 + 2as , s = ut + ½at2 , Ek = ½mv2, F = ma )

• [2007]
• A car of mass 750 kg is travelling east on a level road. Its engine exerts a constant force of 2.0 kN causing the car to accelerate at 1.2 m s–2 until it reaches a speed of 25 m s–1.

Calculate the net force acting on the car.

• Calculate the force of friction acting on the car.
• If the engine is then turned off, calculate how far the car will travel before coming to rest?

Momentum

• [2004][2004 OL][2010 OL]

Define momentum.

• [2004 OL]

Give the unit of momentum.

• [2002][2004 OL][2005 OL][2007 OL][2008 OL][2009 OL][2010 OL]

State the principle of conservation of momentum.

• [2004][2009]

Use Newton’s second law to establish the relationship: force = mass × acceleration.

• [2007 OL][2010 OL]

A rocket is launched by expelling gas from its engines.
Use the principle of conservation of momentum to explain why a rocket rises.

• [2003 OL]

What is the momentum of an object with a mass of 5 kg travelling at 10 m s-1?

• [2007 OL]

Two shopping trolleys each of mass 12 kg are on a smooth level floor.
Trolley A moving at 3.5 m s−1 strikes trolley B, which is at rest.
After the collision both trolleys move together in the same direction.

• Calculate the initial momentum of trolley A
• Calculate the common velocity of the trolleys after the collision.

• [2004 OL]

The diagram shows a child stepping out of a boat onto a pier. The child has a mass of 40 kg and steps out with an initial velocity of 2 m s−1 towards the pier. The boat, which was initially at rest, has a mass of 50 kg.
Calculate the initial velocity of the boat immediately after the child steps out.

• [2002]

A spacecraft of mass 50 000 kg is approaching a space station at a constant speed of 2 m s-1. The spacecraft must slow to a speed of 0.5 m s-1 for it to lock onto the space station.

• Calculate the mass of gas that the spacecraft must expel at a speed 50 m s-1 for the spacecraft to lock onto the space station. (The change in mass of the spacecraft may be ignored.)
• In what direction should the gas be expelled?
• Explain how the principle of conservation of momentum is applied to changing the direction in which a spacecraft is travelling.

•  [2004]

A pendulum bob of mass 10 g was allowed to swing so that it collided with a block of mass 8.0 g at rest on a bench, as shown. The bob stopped on impact and the block subsequently moved along the bench.
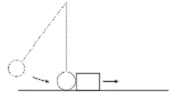The velocity of the bob just before the collision was 2 m s-1.
Calculate the velocity of the block immediately after the collision.

• [2008]

A force of 9 kN is applied to a golf ball by a golf club. The ball and club are in contact for 0.6 ms.
Using Newton’s laws of motion, calculate the change in momentum of the ball.

Mandatory experiments

• [2003 OL]

A student carried out an experiment to investigate the relationship between the force applied to a body and the acceleration of the body. The table shows the measurements recorded by the student.

Force /N	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8
Acceleration /cm s–2	8.4	17.6	25.4	35.0	43.9	51.5	60.4	70.0

 

• Draw a labelled diagram of the apparatus used in the experiment.
• How was the effect of friction reduced in the experiment?
• Describe how the student measured the applied force.
• Plot a graph, on graph paper, of the acceleration against the applied force.
• What does your graph tell you about the relationship between the acceleration of the body and the force applied to it?

 

• [2005 OL]

In an experiment to investigate the relationship between force and acceleration a student applied a force to a body and measured the resulting acceleration. The table shows the measurements recorded by the student.

Force /N	0.1	0.2	0.3	0.4	0.5	0.6	0.7
acceleration /m s–2	0.10	0.22	0.32	0.44	0.55	0.65	0.76

• Draw a labelled diagram of the apparatus used in the experiment.
• Outline how the student measured the applied force.
• Plot a graph, on graph paper of the acceleration against the applied force. Put acceleration on the horizontal axis (X-axis).
• Calculate the slope of your graph and hence determine the mass of the body.
• Give one precaution that the student took during the experiment.

 

• [2006 OL]

In a report of an experiment to verify the principle of conservation of momentum, a student wrote the following:
I assembled the apparatus needed for the experiment. During the experiment I recorded the mass of the trolleys and I took measurements to calculate their velocities. I then used this data to verify the principle of conservation of momentum.

• Draw a labelled diagram of the apparatus used in the experiment.
• How did the student measure the mass of the trolleys?
• Explain how the student calculated the velocity of the trolleys.
• How did the student determine the momentum of the trolleys?
• How did the student verify the principle of conservation of momentum?

 

• [2005]

In an experiment to verify the principle of conservation of momentum, a body A was set in motion with a constant velocity. It was then allowed to collide with a second body B, which was initially at rest and the bodies moved off together at constant velocity.
The following data was recorded.
Mass of body A = 520.1 g
Mass of body B = 490.0 g
Distance travelled by A for 0.2 s before the collision = 10.1 cm
Distance travelled by A and B together for 0.2 s after the collision = 5.1 cm

• Draw a diagram of the apparatus used in the experiment.
• Describe how the time interval of 0.2 s was measured.
• Using the data calculate the velocity of the body A before and after the collision.
• Show how the experiment verifies the principle of conservation of momentum.
• How were the effects of friction and gravity minimised in the experiment?

Exam solutions

• A Force is anything which can cause an object to accelerate.

• A force of 1 N gives a mass of 1 kg an acceleration of 1 m s-2.

 

• Newton’s first law of motion states that an object stays at rest or moves with constant velocity unless an external force acts on it.

• There are no external forces acting on the spacecraft so from Newton’s 1st law of motion the object will maintain its velocity.

 

• Newton’s Second Law of Motion states that the rate of change of an object’s momentum is directly proportional to the force which caused it, and takes place in the direction of the force.

• Newton’s First Law of Motion states that every object will remain in a state of rest or travelling with a constant velocity unless an external force acts on it.

 

• Newton’s laws of motion: see above

• F = ma       Þ        F = 150 × 7 = 1050 N

 

• Gravity (or weight), friction, air resistance.

• W = mg = 120 × 1.6 = 192 N.

 

• Because acceleration due to gravity is greater on the earth (because the mass of the earth is greater than the mass of the moon).

• Because gravity is less on the moon.

 

•  
• W = mg = 2000 × 9.8 = 19600 N
• 2000 kg
• W = mg = 2000 × 1.6 = 3200 N
• The force of gravity is less on moon so less force is needed to escape.

•  
• It accelerates upwards.
• It accelerates forward.
• v = u + at   Þ 0 = 60 + a (120)     Þ a = - 0.5 m s-2
• F = ma       Þ F = 50 000 × 0.5 = 25 000 N.
• They would continue to move at the greater initial velocity and so would be ‘thrown’ forward.

 

• Weight (W) downwards; reaction (R) upwards; force to left (due to friction or curled fingers)

• F = ma = 90 × 0.83 = 75 N Down

 

• Weight acting down.

Air resistance / friction / buoyancy acting up.
Air resistance = weight, therefore resultant force = 0  
Therefore acceleration = 0

• v2 = u2 + 2as          Þ        0 = (2.48)2 + 2a(2)

a = 1.56 m s-2
F = ma = (0.008)(1.6)  = 0. 0.013 N

•  
• v2= u2 + 2as           Þ        (12.2)2 = 0 +2a(25)    Þ        a = 2.98 m s–2
• W = mgsinq = mgsin20 = 234.63 N
• Force down (due to gravity) – Resistive force (due to friction) = Net force

Force down (due to gravity) = 234.63 N
Net force= 70(2.98) = 208.38 N
Friction force = 234.63 – 208.38 = 26.25 N

• v2= u2 + 2as           Þ        u2 = 2g(s)         Þ        s = 5.63 m
• Graph: velocity on vertical axis, time on horizontal axis, with appropriate numbers on both axes.

 

• If the wheelchair is moving at constant speed then the force up must equal the force down, so to calculate the size of the force up, we just need to calculate the force down:

F = mg Sinq
= 900 Sin 10o
= 156.3 N

• Friction is a force which opposes the relative motion between two objects.

 

•  
• v = u + at

50 = 0 + 0.5t
t = 50/0.5 = 100 s

• s = ut + ½ at2 (but a = 0)

s = 50 × (90×60) = 270000 m

• v2 = u2 + 2as

0 = 502 + 2a(500)
a = −2500/1000 = − 2.5 m s-1

• F = ma

F = 30000× (−)(2.5) = - 75000 N = 75 kN

• A = friction/retardation / resistance to motion

B = weight / force of gravity

• The train will move at constant speed.
• See diagram

•  
• Fnet = ma = (750)(1.2)       =          900 N east.
• Fnet = Fcar - Ffriction

900 = 2000 - Ffriction           Þ  Ffriction = 1100 N west

• Friction causes deceleration:  a = F ÷ m

a = (-1100) ÷ 750 = - 1.47 ms-2
v 2 = u 2 + 2as
0 = 25 +2(-1.47) s or s = 213 m

Momentum

 

• Momentum is the defined as the product of mass multiplied by velocity.

• The unit of momentum is the kg m s-1

 

• The principle of conservation of momentum states that in any collision between two objects, the total momentum before impact equals total momentum after impact, provided no external forces act on the system.

• From Newton II: Force is proportional to the rate of change of momentum

F µ (mv – mu)/t    ÞF µ m(v-u)/t                        ÞF µ ma        ÞF = k (ma)    ÞF = ma

• The gas moves down (with a momentum) causing the rocket to move up (in the opposite direction with an equal momentum)

 

• Momentum = mass × velocity = 5 × 10 = 50 kg m s-1.

•  
• (mu = ) 12 × 3.5 =  42 kg m s-1
• Momentum before = Momentum after

42 = m3v3  Þ v3 = 42/m3  Þ        v = 42/24 = 1.75 ( m s-1)

• m1u1 + m2u2 = m1v1 + m2v2           Þ 0 = (40)(2) + (50)x

Þ x = - 1.6 m s-1.

•  
• m1u1 + m2u2 = m1v1 + m2v2

(50000 × 2) = (50000 × 0.5) + (50m)
m =1500 kg

• In what direction should the gas be expelled?

Forward (toward the space station).

• Explain how the principle of conservation of momentum is applied to changing the direction in which a spacecraft is travelling.

As the gas is expelled in one direction the rocket moves in the other direction.

•  m1u1 + m2u2 = m1v1 + m2v2

(0.01)(2) = (0.008) v2
v2= 2.48 m s-1

• From Newton II: Force µ rate of change of momentum

F µ (mv – mu)/t
F = (mv – mu)/t {proportional constant = 1}
(mv – mu) = F × t = (9 × 103)( 0.6 × 10-3) = 5.4 kg m s-1.

 

Mandatory experiments

 

• 
• See diagram in next question.
• Tilt the runway slightly, oil the track.
• By weighing the masses and hanger on an electronic balance.
• See graph
• Acceleration is directly proportional to the applied force.

 

•  
• See diagram.

 

 

 

• Outline how the student measured the applied force.

The applied force corresponds to the weight of the hanger plus weights; the value of the weights is written on the weights themselves.

• Plot a graph, on graph paper of the acceleration against the applied force. Put acceleration on the horizontal axis (X-axis).

See graph.

 

 

• 

Substituting in two values (from the graph, not the table) should give a slope of approximately 0.9.
This means that the mass = 0.9 kg.

• Oil the trolley wheels, dust the runway, oil the pulley.

 

 

 

 

 

 

 

•  
• See diagram
• By using an electronic balance.
• By taking a section of the tape and using the formula velocity = distance/time. We measured the distance between 11 dots and the time was the time for 10 intervals, where each interval was 1 50th of a second.
• Using the formula momentum = mass × velocity.
• By calculating the total momentum before and afterwards and showing that the total momentum before = total momentum after.

 

 

• 
• See diagram
• It corresponded to 10 intervals on the ticker-tape.
• Velocity before:  v = s/t = 0.101/0.2

v = 0.505 m s-1  ≈ 0.51 m s-1
Velocity after: v = 0.051/0.2
v = 0.255 m s-1 ≈ 0.26 m s-1

• Momentum before:

p = mv = (0.5201)(0.505) = 0.263 ≈ 0.26 kg m s-1
Momentum after:
p = mv = (0.5201 + 0.4900)(0.255)
p = 0.258 ≈ 0.26 kg m s-1
Momentum before ≈ momentum after

• Friction: sloped runway // oil wheels or clean track

Gravity: horizontal track // frictional force equal and // tilt track so that trolley moves with constant velocity

[2010 OL]
You carried out an experiment to investigate the relationship between the acceleration of a body and the force applied to it.
You did this by applying a force to a body and measuring the resulting acceleration.
The table shows the data recorded during the experiment.

 

Force / N	0.20	0.25	0.30	0.35	0.40	0.45	0.50
acceleration / m s−2	0.4	0.5	0.6	0.7	0.8	0.9	1.0

 

 

• Draw a labelled diagram of the apparatus you used

Labelled diagram to show:
Trolley / rider
Runway / air-track
Means of applying a force e.g. string over pulley to weight on pan
Means of measuring acceleration e.g. 2 photo-gates (and timer) // tickertape (and timer)

• How did you measure the applied force?

Weighed the mass (and pan) / mg // from the (digital Newton) balance

• How did you minimise the effect of friction during the experiment?

Slant/clean the runway // oil (the trolley) wheels / frictionless wheels

• Plot a graph on graph paper of the body’s acceleration against the force applied to it

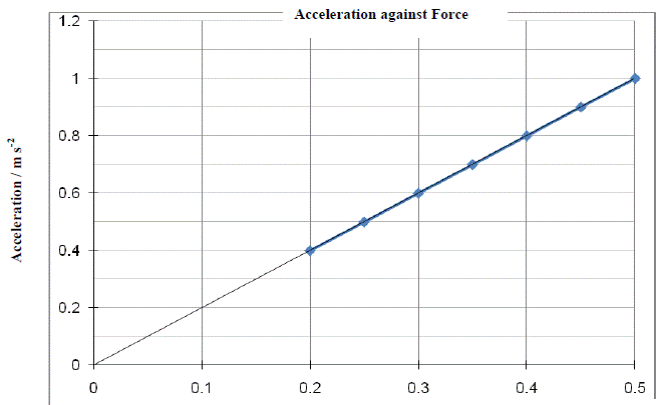
• What does your graph tell you about the relationship between the acceleration of the body and the force applied to it?

They are proportional.

 

[2010 OL]

• An ice skater of mass 50 kg was moving with a speed of 6 m s−1 then she collides with another skater of mass 70 kg who was standing still. The two skaters then moved off together.

Calculate the momentum of each skater before the collision?
50 × 6 = 300 kg m s−1
70 × 0 = 0 kg m s−1

• What is the momentum of the combined skaters after the collision?

300 kg m s−1

• Calculate the speed of the two skaters after the collision.

300 = (50 + 70) v
v = 2.5 m s−1

 

[2010 OL]
A cyclist on a bike has a combined mass of 120 kg.
The cyclist starts from rest and by pedalling applies a net force of 60 N to move the bike along a horizontal road.
Calculate the acceleration of the cyclist
F = ma, a = 60/120
a = 0.5 m s–2

[2010 OL]
A cyclist stops peddling and continues to freewheel before coming to a stop. Why does the bike stop?
Due to friction / air resistance.

 

 

[2010]
In an experiment to investigate the relationship between the acceleration of a body and the force applied to it, a student recorded the following data.

 

F/N	0.20	0.40	0.60	0.80	1.00	1.20	1.40
a/m s–2	0.08	0.18	0.28	0.31	0.45	0.51	0.60

 

• Describe the steps involved in measuring the acceleration of the body.

Measure/calculate the initial velocity/speed
Measure/calculate the velocity/speed again (t seconds later)
Measure time interval from initial to final velocities / distance between light gates
Use relevant formula

Datalogging method:
Align motion sensor with body (e.g. trolley) / diagram
Select START and release body
(Select STOP and) display GRAPH of ‘a vs. t’ // ‘v vs. t’
(Use tool bar to) find average value for a // use slope (tool) to find  a (= dv /dt)

 

• Using the recorded data, plot a graph to show the relationship between the acceleration of the body and the force applied to it.

Label axes correctly on graph paper
Plot six points correctly 
Straight line
Good distribution

• What does your graph tell you about this relationship?

Acceleration is proportional to the applied force.

• Using your graph, find the mass of the body.

 The mass of the body corresponds to the slope of the graph =  2.32 kg [range: 2.1 - 2.4 kg]

• On a trial run of this experiment, a student found that the graph did not go through the origin.

Suggest a reason for this and
Friction / dust on the track slowing down the trolley.

• Describe how the apparatus should be adjusted, so that the graph would go through the origin.

Elevate/adjust the track/slope

 

 

 

Source : http://www.thephysicsteacher.ie/LC%20Physics/Student%20Notes/9.%20Force,%20Mass%20and%20Momentum.doc

Web site link: http://www.thephysicsteacher.ie

Author : not indicated on the source document of the above text

If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.

 

 

Force mass and momentum

 

 

Force mass and momentum

 

Main page

 

Alimentation - nutrition	Animals	Architecture	Art
Astrology, esoteric, parapsychology and fantasy	Astronomy	Biology and genetics	Botany and agriculture
Chemistry	Courses, training, guides, handbooks and tips	Culture General and actuality	Dermatology, health and wellness
Dictionaries and glossaries	Economics and finance	Education and pediatrics	Engineering and technology
English grammar and anthology	Fashion and show business	Fitness	Food, recipes and drink
Games, play space	Geography, geology and environment	History	Informatics and computer world
Jobs world	Languages	Leisure and DIY do it yourself	Lessons for students
Literature, biographies and journalism	Mathematics, geometry and statistical	Medicine	Music
Notes and concept maps	Philosophy	Photography and images - pictures	Physics
Physiology	Psychology and psychoanalysis	Quiz questions and answers	Religions
Rights law and political science	Science	Sociology and cultural anthropology	Sport
Summaries and reviews	Television, film - movies and comics	Theater and communications	Theses, themes and dissertations
Travel and tourist guides	Useful documents and tables	Utility, calculators and converters	Weather and meteorology

 

 

This is the right place where find the answers to your questions like :

Who ? What ? When ? Where ? Why ? Which ? How ? What does Force mass and momentum mean ? Which is the meaning of Force mass and momentum?

 

---

 

---

 

 

 

Alanpedia.com from 1998 year by year new sites and innovations

Main page - Disclaimer - Contact us