Gravitation and Newton' s law of gravity
Gravitation and Newton' s law of gravity
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Gravitation and Newton' s law of gravity
Newton's Law of Gravity
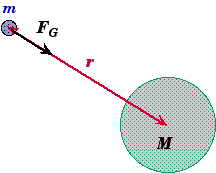
- Between any two objects that have mass, there exists an attractive gravitational force acting on each object separately. These two forces have the same magnitude but are in opposite directions.
- When the two objects have spherical mass distributions (or are point masses), then the gravitational force acts along a line connecting the center of mass of each of the two objects.
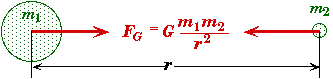
FG |
= Magnitude of the Gravitational Force (N) |
m1 |
= Mass of one body (kg) |
m2 |
= Mass of a second body (kg) |
G |
= 6.672x10-11 N.m2/kg2 (Universal Gravitational Constant) |
r |
= Distance between the centers of mass of the two objects (m) |
- The gravitational force does not depend upon the size or the density of the two bodies, provided their mass distribution is spherical. Nor does it even depend upon the speed of motion of the two bodies. It only depends upon their separation and masses.
- The origin is usually taken to the center of one mass or the other mass. By do so we know that the direction of the force exerted is radial towards the origin.
- We call G a universal constant because we believe that it has the same value no matter where the two bodies are located either in the universe or in the age of the universe. Comparison of the Four Fundamental Forces. It is interesting to note that the gravitational force is the weakest of the four forces yet it holds the universe together on its largest scale.
Non-Spherical Mass Distributions:
When a body has an irregular shape, we can use calculus to determine the gravitational force. The force between two infinitesimally small masses (dm1 and dm2) will obey the gravitational force law
![]()
We can integrate this equation over all the mass in the two bodies to determine the total gravitational force. In general, the gravitational force does not act between the center of mass of irregularly shaped objects.
Normally we do not have to worry about this because the gravitational force between to human size objects in negligible. Moreover, when objects get larger enough (like the size of a planet) gravity itself causes them to become round.
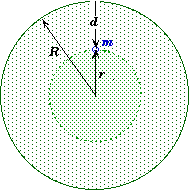
Gravitational Force inside a Spherical Mass Distribution:
- Using the differential form above, Newton showed that if a mass object is located inside a spherical mass distribution then the gravitational force is only due to the mass in a sphere closer to the center than that of a small mass inside the sphere.
- For example, if you dug a deep hole, then the gravity acting on a small mass at the bottom of the hole would only be due to the mass of the Earth below the bottom of the hole. The gravitational force of the mass of the Earth above the bottom of the hole cancels out, i.e. its net vector sum adds up to zero.
Acceleration of Gravity
At any distance r from a large circular body of mass M a smaller body of mass m will experience a gravitational force.
|
Applying Newton's Second (Fnet = ma) to the small object we can determine its acceleration if no other force are acting on the small mass m but gravity (Fnet = FG).
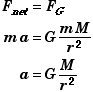
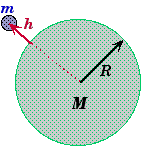
Acceleration of Gravity Near the Surface of a Large Body
Assume that a large body of mass M and radius R has a radically uniform mass distribution. The gravitational force on a small mass m at height h above the surface of the large body can be expressed as,
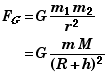 |
|
If h << R, then![]()
If we neglect air resistance, then this is the net force acting on the mass m. Applying Newton's Second Law, Fnet = ma,
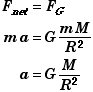
Because of its importance we usually give the acceleration of gravity due to the Earth a separate name,
![]()
* This equation does not depend upon the mass of the small object - the mass canceled out on both sides of the force equation. This proves that the acceleration due to gravity alone is the same on all objects independent of their mass, their size, their density, or even their speed.
* Local concentrations of mass in the Earth can change the magnitude of the acceleration of gravity in the third significant figure. In fact, it is often true that as you go up a mountain the vale of g gets larger not smaller as you would expect because mountains contain a larger concentration of denser rocks.
* Since the value of g is not a fixed constant, in this course we will normally use 9.80 m/s2 when solving problems.
Acceleration of Gravity at the North Pole
The Earth's polar radius is 6356 km and its mass is 5.9736x1024 kg.
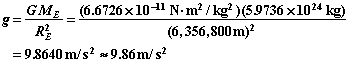
Acceleration of Gravity at the Equator
The Earth's equatorial radius is 6378.1 km. Neglecting the Earth's rotation,
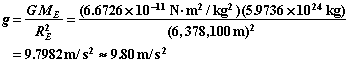
The Earth is also rotating so that the acceleration of gravity at the equator will be reduced by the centripetal acceleration. Since these are both along the same direction (radially) at the equator we don't have to subtract them vectorially - just numerically,
![]()
Since the Earth makes one revolution per day, w = 2p rev/day
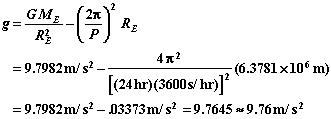
Weight as Function of Latitude:
If you are at some latitude F above the equator then your period of rotation will still be one day, but your distance from the axis of rotation will be reduced to R cos(F). This reduces the effect of the centripetal acceleration. Moreover the Earth is not a perfect sphere, so R will also change.
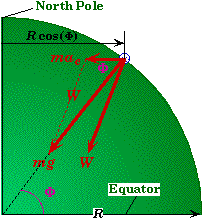
Assuming a spherical Earth we can determine the weight on a mass m at a latitude F. By applying the law of cosines to the force vectors we get
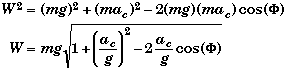
Where
![]()
For Los Angeles CA, F = 34.18 , and the centripetal acceleration is ac = .02223 m/s2. This gives an effective gravity of
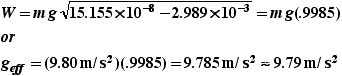
A value that the student's here a Mt. Sac have consistently found when measuring the acceleration of gravity over the pasted 30 years. There are other factors that could effect the local value of g such as elevation above sea level and the local concentrations of denser rock.
Kepler's Three Laws of Planetary Motion
- The shape of the orbit of any body (be it an asteroid, planet, comet, or space craft) orbiting the Sun is an Ellipse with the Sun at one of the foci.
- More generally, the orbit of any two bodies about each other can be reduced the to that of one body orbiting about the other in an elliptical orbit with the other body at the focus of the ellipse. (We will discuss binary stars later in the course)
- This law is a consequence of the fact that Newton's law of gravity varies as one over distance squared.
Importance:
This law can be used to determine a planet's location r at any position of the planet relative to the Sun.
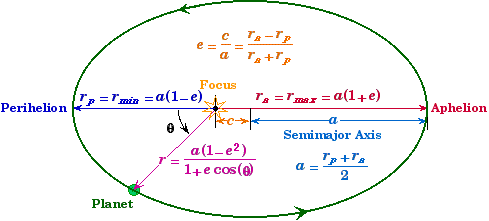
r |
= Distance of the planet from the Star (SI: m) |
q |
= Angular location of the Planet from measured from Perihelion (SI: rad) |
a |
= Semimajor Axis "Mean Size of the Orbit" (SI: m) |
c |
= Distance of the Star/Focus from Center (SI: m) |
e |
= Eccentricity "Measures the out-of-roundness of the Orbit" (dimensionaless ratio) |
rp |
= Perihelion distance "Closest Approach to Star" (SI: m) |
ra |
= Apohelion distance "Maximum Separation from Star" (SI: m) |
- The origin is located at the center of the primary body - the Sun - for the above equations.
2. Law of Areas
* The line joining the planet to the Sun sweeps out equal areas in equal times.
- This law is a consequence of the conservation of angular momentum applied to the orbiting body.
Importance:
This law can be used to determine a uniform passage of time. This method (called Ephemeris time) was for many years the basis of our most accurate time keeping method before the use of atomic clocks replaced it.
Conservation of Angular Momentum:
Since the gravitational force is always directed radially through the center of mass, the gravitational force can exert no torque on either body. Thus angular momentum is conserved. This means that the angular momentum of the orbiting object will always have the same value at any point in its orbit.
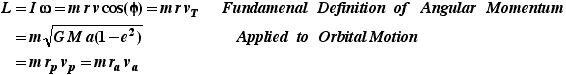
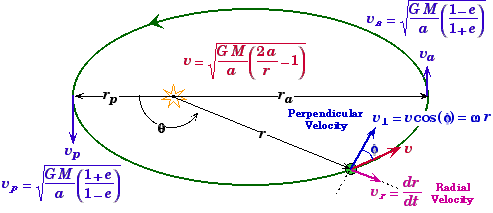
- For the velocities see Orbital Velocities.
3. Harmonic Law
* The square of the sidereal orbital period of a body is proportional to the cube of the planets mean distance from the Sun.
- This law is a consequence of the fact that the object is in a bound orbit about the sun that varies as one over r2.
Importance:
Of its many uses, a primary one is the determination of the mass of a star or planet directly from information about the period and distance of an orbiting object.
![]()
P |
= Sidereal Period of the planet "Planet Year" (SI: sec) |
a |
= Semimajor Axis of the orbit ( SI: m) |
M |
= Mass of the Star (SI: kg) |
Simplified Version (Change of Units Equation):
![]()
For objects orbiting the Sun their distances are often measured in Astronomical Units (1 AU = the mean Earth-Sun distance = 1.49x1011 m = the Earth's semimajor axis). Typical orbital periods are on the order of years. In a set of units that measures distance in AU, time in years, and the mass of the central star in solar masses (1.989x1030 kg), the value of 4p2/G = 1.
Example Problems:
1. Estimate the force of attraction between a 50 kg woman and a 70 kg man sitting 1.0 m apart:
Model: Model the woman (w) and the man (m) as spherical masses or particles.
Solve: ![]()
2. Two spherical objects have a combined mass of 150 kg. The gravitational attarction between them is 8.00 * 10-6 N when their centers are 20 cm apart. What is the mass of each?
Solve: We are given![]() We also have
We also have
![]()
Thus, ![]() Solving this equation gives
Solving this equation gives ![]() and
and ![]() The two masses are 104 kg and 46 kg.
The two masses are 104 kg and 46 kg.
3. a. At what height above the earth is the acceleration due to gravity 10% of its value at the surface?
b. What is the speed of a satellite orbiting at that height?
Model: Model the earth (e) as a spherical mass and the satellite (s) as a point particle.
Visualize: Let h be the height from the surface of the earth where the acceleration due to gravity (galtitude) is 10% of the surface value (gsurface).
Solve: (a) Since galtitude = (0.10) gsurface, we have
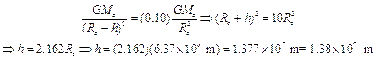
(b) For a satellite orbiting the earth at a height h above the surface of the earth, the gravitational force between the earth and the satellite provides the centripetal acceleration necessary for circular motion. For a satellite orbiting with velocity vs,
![]()
Source: http://physics.mtsac.edu/4A/4A%20Text/gravitation.doc
Web site link : http://physics.mtsac.edu/
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Gravitation notes
Gravitation and Newton' s law of gravity
Gravitation and Newton' s law of gravity
Gravitation and Newton' s law of gravity
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Gravitation and Newton' s law of gravity mean ? Which is the meaning of Gravitation and Newton' s law of gravity?
Gravitation and Newton' s law of gravity physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us