Harmonic motion
Harmonic motion
The following text is used only for educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Harmonic motion
We have been dealing with straight line motion or motion that is circular. There are other types of motion that must be dealt with. Specifically a motion that repeats itself over and over. Such a thing has its very own phancy physics name. “The name?” the desperately curious, interested advanced physics student asks? It is called, dear student, periodic motion.
Periodic Motion º motion in which a body moves back and forth with a fixed path over a definite interval of time.
A special case of periodic motion is known as harmonic motion.
Harmonic Motion º Periodic motion with no friction that is produced by a restoring force that is directly proportional to the displacement and oppositely directed.
Don’t you hate definitions like that? The Physics Kahuna is so sorry, but what can you do?
Let’s see how it works, which is really the best way to learn about it.
Okay, see, the uh, restoring force pushes and or pulls the object undergoing the harmonic motion and is the thing that makes it happen.
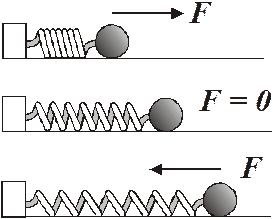
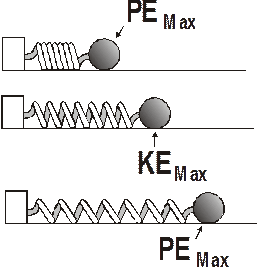
Let’s look at a simple example of harmonic motion. A sphere is attached by a spring to a solid block. The sphere (and spring) is free to slide back and forth on a smooth, frictionless surface.
The drawing above gives you an idea of the sequential motion of the system. Initially the spring is compressed. This is shown in the first drawing. The ball is released and the spring pushes it outward. In the second drawing, the spring has reached its normal displacement and is no longer exerting a force on the ball. Ah, but the ball’s inertia and the good old first law ensure that the ball keeps moving. As it does this, it stretches the spring. Of course this causes the spring to exert a force in the opposite direction which slows the ball. This is the restoring force. Anyway, eventually the spring force has had enough time to stop the ball. This is depicted in the third drawing. Once the ball stops, the spring will pull it back in the opposite direction and the process will repeat itself.
Here are some critical terms that have to do with such motion.
Equilibrium position º this is the point in the motion where the object would be if it were not subject to any forces.
Amplitude (A) º The maximum displacement from the equilibrium position.
Cycle º One complete iteration of the motion sequence.
Period (T ) º The time it takes to do one cycle.
Frequency ( f ) º The number of cycles per unit of time.
The drawing below gives us a depiction of the amplitude of the system.
A simple way to understand this motion is to look at a graph of displacement vs time. The graph looks like this:
The displacement is plotted along the y axis and time is plotted along the x axis. The amplitude is the maximum displacement value. On the graph, one cycle is the segment of the curve from in phase point to the next sequential in phase point. In phase points? Okay, okay already. These are points along the displacement path where the object is doing the same thing.
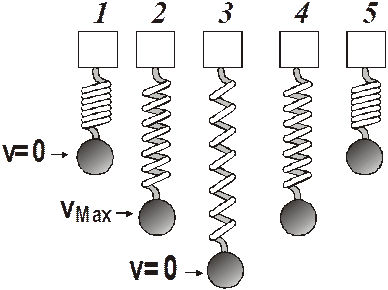
No better way to understand the thing than to look at another example. Here we have us a weight attached to a vertically mounted spring. The weight is given an initial small displacement (which will be the amplitude) and then released. It bobs up and down. Its velocity will vary as it moves through the cycle. The velocity is zero at the top of the motion and at the bottom. The maximum velocity occurs at the zero displacement position.
Acceleration and displacement: We can analyze the motion more fully by looking at the forces in the system, the accelerations that are taking place, and the displacement.
We begin with Hooke’s law, which we studied when we dealt with energy. This is the force that is exerted by the spring.
Hooke’s Law 
Recall that the minus sign simply means that the force exerted by the spring is always opposite to the displacement.
The maximum force will occur at the maximum displacement, which is the amplitude, so we can write an equation for the maximum force.
Where FMax is the maximum restoring force, k is the spring constant and A is the amplitude.
We can now apply the second law to find the maximum acceleration.
We can plug 
into the acceleration equation we just developed:
Theacceleration is not constant because the force is not constant. We can write an equation for the acceleration as a function of displacement.
At zero displacement, the acceleration will be zero, since, as you can see, the displacement x is zero. The acceleration is varying then between its maximum value, which takes place at the maximum displacement (the good old amplitude) and zero.
The acceleration ranges from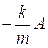 
to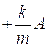 
. In between it is given by: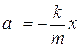 
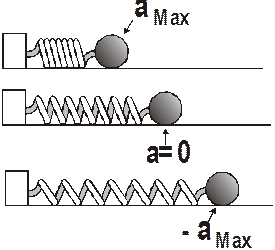
In the drawing above, we can see the positions that have the maximum acceleration. We have chosen the coordinate system so that an acceleration to the right is positive and an acceleration to the left is negative.
Another important ideas is that the initial displacement given the system – we could call this the release point – will determine the amplitude. So you pull the spring out and give it a displacement of 5.0 cm, that means that the amplitude has to be 5.0 cm. Do you see why this is so?
- A spring has a constant of 125 N/m. A 350.0 g block is attached to it and is free to slide horizontally on a smooth surface. You give the block an initial displacement of 7.00 cm. What is (a) the maximum force and (b) the maximum acceleration acting on the block?
- To find the force we use Hooke’s law:
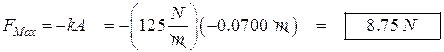
Note that the Physics Kahuna cleverly gave the thing a negative displacement so it would all come out positive.
- To find the acceleration we use the second law:
Relation Between Frequency and Period:
The frequency of the system is the number of cycles per unit time. We can write an equation for this:
Therefore:
f is the frequency and T is the period.
Also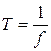 
The unit for frequency is the Hertz. (It used to be a cps, a cycle per second, i.e., 
, but they changed it back in the turbulent 60’s.)
- The period of a system is 0.00210 s. What is its frequency?
Energy and Amplitude: The total energy of a system undergoing harmonic motion must, by law, remain constant. But of course the type of energy can be transformed from one type or types to another.
Clearly the energy of the system must be all potential energy when the displacement is at its maximum value. This is because the velocity of the system is zero. This will occur when the displacement is equal to the amplitude. Once the mass is moving away from maximum displacement, some of the potential energy is converted to kinetic energy. The kinetic energy increases and the potential energy decreases until the displacement is zero. At this point all the energy is kinetic and the object is moving at maximum speed. The kinetic energy then begins to decrease and the potential energy increases until the amplitude is reached again. And so on. It looks like this:
The potential energy for a spring is given by this equation: (the Physics Kahuna is positive that you remember the equation with joy)
If we plug in the amplitude for the displacement, we get an equation for the energy of the system.
This is the maximum amount of energy that the system can have – the system will get no other energy.
The Law of Conservation of Energy tells us that the total energy of the system must remain constant, so this equation gives us the energy that the system has at any point in the cycle.
Also not that the energy is proportional to the square of the amplitude.
We can plot kinetic energy vs time, potential energy vs time, and displacement vs time and then compare them.
When we do this, we get three graphs that look like this:
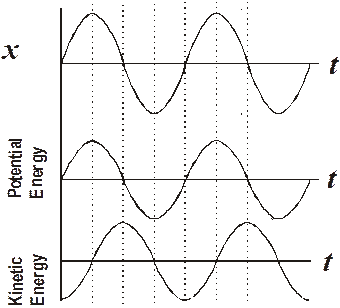
You should be prepared to mark up a drawing or a graph of a harmonic motion situation and locate the places where the kinetic energy is at a maximum or minimum, the potential energy’s maximum and minimum values, where the velocity is zero or maximum, where the acceleration is minimum or maximum, and where the forces are minimum or maximum.
Calculating Energy: From the law of conservation of energy, we know that the energy must stay constant for the system This means that:
But since we are ignoring gravitational potential energy, the expression is simplified to:
We also know that the total energy of the system must be:
The energy of the system for any displacement must be:
Period of spring system: The period for a spring system moving with a small displacement is given by this equation. (You will be provided with this equation on the AP Physics Test).
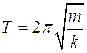
T is the period, m is the mass of the weight (we are ignoring the mass of the spring, as it is usually insignificant), and k is the spring constant.
- A 345 g block is part of a spring system, is oscillating. The spring constant is 125 N/m. What is the period of the system?
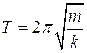
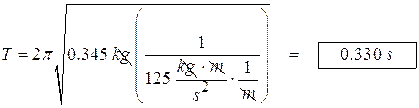
In the real world, we have to deal with friction and energy losses, so that the actual graph would look like this:
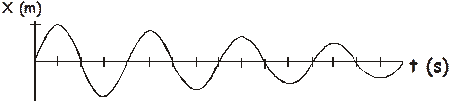
The amplitude decreases over time, although the period and frequency do not change. This decrease in amplitude deal is called dampening or attenuation (takes your pick). We will, in solving our little problems, ignore this dampening effect.
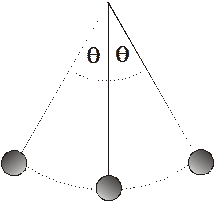Period of a Pendulum:
Another simple harmonic system is a pendulum. The period of a pendulum is constant for small angle swings (for large angle swings, the period is not a constant). Galileo is credited with the discovery that the pendulum period is constant. He supposedly did this in a cathedral. Apparently not paying as much attention to the priest as church officials would desire, he grew bored and noticed that a chandelier was swinging back and forth. Using his pulse as a timing device, he discovered that the chandelier took the same amount of time to make each swing regardless of how big the swing was. Later he used pendulums to time his experiments. Eventually pendulums were used to regulate the motion of clocks. This led to the first accurate clocks. (One can argue that this led to the horrible, frantic modern world with its insane preoccupation with time, but he Physics Kahuna will not go there.)
The period of a pendulum is given by this formula (which will also be available to you on the AP Physics Test).
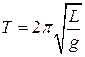
T is the period, L is the length of the pendulum, and g is the acceleration of gravity.
Note that the period of a pendulum depends only on its length.
Pendulums are commonly used to experimentally find a value for g, the acceleration of gravity in physics experiments. How would you go about doing that?
- A tall tower has a cable attached to the ceiling with a heavy weight suspended at its bottom near the floor. If the period of the pendulum is 15.0 s, how long is the cable?
This is a simple problem – we use the period equation and solve it for the length of the pendulum.
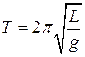
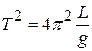
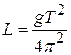
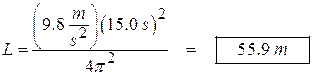
Source : http://teachers2.wcs.edu/high/bhs/mikek/AP%20Physics%20Course%20Notes/Waves/1%20-%20Harmonic.doc
Web site link: http://teachers2.wcs.edu
Author : not indicated on the source document of the above text
Harmonic motion
Harmonic motion
Harmonic motion
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Harmonic motion mean ? Which is the meaning of Harmonic motion?
Harmonic motion physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us