Quantity of Heat and Heat Transfer

The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.

We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge

Physics

Quantity of Heat and Heat Transfer

Heat is a form of energy that can cause a rise in temperature when added or a fall in temperature when withdrawn.

The Specific Heat Capacity* of a substance is the heat energy needed to change one kilogram of the substance by one Kelvin.
The symbol for Specific Heat Capacity is c.

Its unit is the Joule per kilogram per Kelvin (J kg-1 K-1).

Q = mcrq

Change in Heat Energy = (Mass)(Specific Heat Capacity)(change in Temperature)

rq (representing change in temperature) is pronounced “delta theta”*
See Worked Problems 1- 4, page 160/161 then try questions 4 – 11, page 162.

Storage Heaters

In an electric storage heater, bricks with a high specific heat capacity are heated overnight by passing an electric current through a heating coil in the bricks. The bricks are surrounded by insulation.
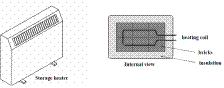The bricks are heated by night when electricity is cheaper.
The system is closed in but has a cover which can be opened to release the heat when needed.
During the day the bricks slowly give out their heat, thus heating the room.
Because the bricks have a high specific heat capacity they can absorb a lot of heat without increasing very much in temperature, therefore not losing much back to the environment.

heat

Latent Heat

Graph of Temperature versus Time for water: Latent Heat Curve:*
At the melting and boiling points, the energy taken in is used to change the state of the substance rather than causing an increase in temperature.
Once all the substance has changed state then the temperature begins to rise again.

The Specific Latent of Fusion (lf) of a substance is the amount of heat energy need to change 1 kg of the substance from a solid to a liquid without a change in temperature.

The Specific Latent of Vaporisation (lv) of a substance is the amount of heat energy needed to change 1 kg of the substance from a liquid to a gas without a change in temperature.

The unit of Specific Latent Heat is the Joule per kilogram (Jkg-1).
Note that there is no reference to Kelvin in this unit.
This is because there is no temperature change.

Q = ml

Formula for Latent Heat
Heat needed to change state = Mass × Specific Latent Heat

The Heat Pump is a device that extracts available heat from one area and transfers it to another to either heat or cool an interior space.
Examples: 1. Refrigerator* 2. Perspiration*.

Heat Transfer*
Three methods of Heat Transfer: 1. Conduction 2. Convection 3. Radiation

1. Conduction is the movement of heat energy through a substance by the passing on of molecular vibration from molecule to molecule, without any overall movement of the substance.
You are expected to be able to demonstrate how to compare rates of conduction through different solids (Junior Cert)

U-Value*
The U-value of a house is a measure of the rate of heat loss to the surroundings.

U-Values are used in domestic situations to give an indication of how well a substance (roof, walls, tiles, etc) allows heat to flow (conduct) through it.
U-Values are a measure of the conductivity of a substance, i.e. a structure that is a good insulator has a low U-Value.
The U-Value of a structure is the amount of heat energy conducted per second through 1 square metre of that structure when a temperature difference of 10 C is maintained between its ends.
heat
2. Convection is the transfer of heat through a fluid by means of circulating currents of fluid caused by the heat.
Because hot water expands, it is less dense than cooler water and so rises.
This principle is used in domestic hot water and heating systems.

3. Radiation is the transfer of heat energy from one place to another in the form of electromagnetic waves.

Leaving Cert Mandatory Experiments:
Measurement of Specific Heat Capacity of Water
Measurement of the Specific Latent Heat of fusion of ice
Measurement of the Specific Latent Heat of Vaporisation of water

THAT’S ALL FOLKS!!

Leaving Cert Physics Syllabus

Content	Depth of Treatment	Activities	STS

Concept of heat.	Heat as a form of energy that causes a rise in temperature when added or a fall in temperature when withdrawn.
QUANTITY OF HEAT
1. Heat capacity, specific heat capacity	Definitions and units.	Appropriate calculations.	Storage heaters.
2. Latent heat, specific latent heat.	Definitions and units.	Appropriate calculations.	Heat pump, e.g. refrigerator, perspiration.
HEAT TRANSFER
1. Conduction	Qualitative comparison of rates of conduction through solids.	Simple experiments.	U-value; use in domestic situations.
2. Convection		Simple experiments.	Domestic hot-water and heating systems.
3. Radiation	Radiation from the sun.	Simple experiments.	Everyday examples. Solar heating.

MEASUREMENT OF THE SPECIFIC HEAT CAPACITY OF WATER

APPARATUS
Power supply, joulemeter, heating coil, calorimeter, thermometer, electronic balance.
heat
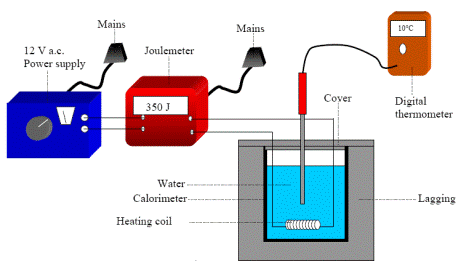
DIAGRAM

PROCEDURE

Find the mass of the water by first measuring the mass of the empty calorimeter, then the mass of the calorimeter with water in it, and subtracting one form the other.
Set up the apparatus as shown in the diagram (with a power supply connected to the joulemeter).
Record the initial temperature of the water (we assume this to be the same temperature as the calorimeter).
Switch on the power supply and allow the temperature of the water to rise by about 10 degrees.
Switch off the power supply.
Note the reading on the joulemeter and the final temperature of the water (and calorimeter).
Calculate the specific heat capacity of water (cwater) using the equation:

Energy supplied = (mcΔθ)cal + (mcΔθ)water

where Δθ is the change in temperature and ccal is known.
****************************************************************
RESULTS
Mass of calorimeter:
Mass of calorimeter + water:
Mass of water:
Initial temperature of water (and calorimeter):
Final temperature of water (and calorimeter):
Change in temperature Δθ:
Joulemeter reading:

CONCLUSION
The theoretical value for the specific heat capacity of water = 4200 J kg–1 K–1. We got an answer of 7.
Conclusion? I need to start copying my answers from someone else.

SOURCES OF ERROR

Heat may be gained from or lost to the surroundings.
If a mercury thermometer is used, this may only be accurate to the nearest degree.

PRECAUTIONS

Ensure that the heating element is covered with water to avoid any loss of heat energy.
Ensure that the calorimeter is well insulated to avoid loss of heat energy.
Stir the water throughout the experiment to ensure that the thermometer reading reflects the heat supplied.
Use a sensitive thermometer graduated to 0.1 or 0.2 degrees. An error of 1 deg. in 10 is a large percentage error.
Ensure that room temperature is midway between the initial and final temperatures of the water.

NOTE
What you are not told in the text-book is that all these ‘Heat’ experiments are notoriously inaccurate due to heat loss. Personally I think anything within 33% of the correct value is great. But then I never was much good at Physics.

MEASUREMENT OF THE SPECIFIC LATENT HEAT OF FUSION OF ICE

APPARATUS: Ice, water, calorimeter, lagging, beakers, kitchen paper, thermometer and electronic balance.
heat
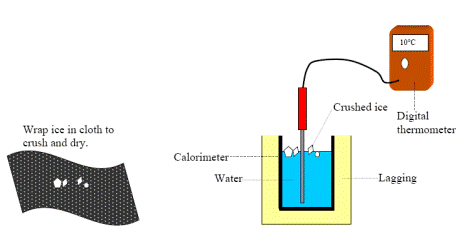
DIAGRAM:

PROCEDURE

Place some ice cubes in a beaker of water and keep taking the temperature with the thermometer until the ice-water mixture reaches 0 °C.
Find the mass of the calorimeter.
Half fill the calorimeter with water.
Find the combined mass of the calorimeter and water ice. The mass of the water can be calculated by subtraction.
Find the mass of the beaker and its contents. The mass of the ice can be calculated by subtraction.
Record the initial temperature (θinitial) of the calorimeter plus water.
Crush some ice and dry it carefully with blotting paper or filter paper.
Add the pieces of dry crushed ice to the calorimeter. Do this until the temperature of the water has fallen by about 10 °C.
Take a note of the lowest temperature reached (θfinal)
Use the formula below to calculate a value for the latent heat of fusion of ice.

RESULTS
Mass of calorimeter:
Mass of calorimeter plus water:
Room temperature:
Temperature of ice:
Initial temperature of water (θinitial):
Final temperature of water (θfinal):
Mass of calorimeter plus water plus ice:

CALCULATIONS
The rise in temperature of the ice (θΔmelted ice) = θfinal – 0 °C . . . . . . . . . . .
The fall in temperature of the calorimeter (Δθcal) = is θinitial – θfinal . . . . . . . . . . . .
The fall in temperature of the water (Δθwater) = is θinitial – θfinal . . . . . . . . . . . .
Mass of water:
Mass of ice:
We now have
Heat lost by calorimeter + heat lost by water = Heat gained by ice turning to water + heat gained by melted ice

(mcΔθ)cal + (mcΔθ)water = (ml)ice + (mcΔθ)melted ice

CONCLUSION
The theoretical value for specific latent heat of fusion of ice is 3.3 × 105 J kg-1. We got a value of 7, so obviously either the theory is crap or I need a new lab partner.

PRECAUTIONS

Ensure that the ice is dried (dab it with tissue paper) before adding to the calorimeter.
Use warmed water (about 10 deg. above room temp.) at the start of the experiment so that, on average, heat is neither lost or gained from the surroundings. This also helps the ice to melt more quickly speeding up the expt.
Use a well insulated calorimeter to avoid loss or gain of heat to the surroundings.
Stir well and record the lowest temperature when all of the ice has melted.

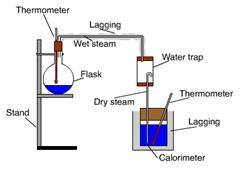
MEASUREMENT OF THE SPECIFIC LATENT HEAT OF VAPORISATION OF WATER

APPARATUS
heat Calorimeter, beaker, conical flask, steam trap, retort stand, heat source, thermometer, electronic balance.

DIAGRAM

PROCEDURE

Find the mass of the calorimeter.
Half fill the calorimeter with water.
Find the mass of the water plus calorimeter and by subtraction find the mass of the water.
Record the temperature of the calorimeter plus water θinitial
Boil the water in the flask until steam issues freely from the delivery tube.
Allow dry steam to pass into the water in the calorimeter until the temperature has risen by about 20 °C, then remove the steam delivery tube from the water.
Record the final temperature θfinal of the calorimeter plus water plus condensed steam.
Find the mass of the calorimeter plus water plus condensed steam and by subtraction find the mass of the condensed steam.

RESULTS
Mass of the calorimeter........................... =
Mass of calorimeter plus cold water .................................. =
Initial temperature of water..................... =
Temperature of the steam........................ =
Final temperature of water ...................... =
Final mass of steam calorimeter plus water plus steam ............................... =

CALCULATIONS
Mass of cold water .................................. =
Mass of steam .................................. =
Δθcondensed_steam = . . . . . . . .
Δθcal = . . . . . . . . . . . . .
Δθwater = . . . . . . . . . .
Energy lost by steam + energy lost by condensed steam cooling down = energy gained by calorimeter + energy gained by the water
mlsteam + mcΔθcondensed_steam = mcΔθcal + mcΔθwater

CONCLUSION:
The theoretical value for the latent heat of vapourisation of water is 2.26 x 106 J kg-1; we got an answer of 7. Therefore we conclude that this experiment sucks.

PRECAUTIONS:

Ensure that only steam (not water) enters the water in the calorimeter. Use a "steam trap" (it actually traps water) if available
Use a tilted insulated tube as an alternative delivery pipe for dry steam. This does away with the need to use a steam trap.
If the water in the calorimeter is initially cooled to10 °C below room temperature and then heated to 10 °C above room temperature the heat gains and heat losses approximately cancel each other out.
Use a well insulated calorimeter to avoid loss or gain of heat to the surroundings
Stir well and record the highest temperature when the steam has stopped bubbling into the water.

Extra Credit

*Specific Heat Capacity

It doesn’t matter if the object is being heated from 20 C to 30 C, or from 920 C to 930 C; each is an increase of 10 C and therefore the same amount of heat energy is required in both cases.
Basically, if a substance has a high s.h.c. a lot of heat is required to change its temperature.

If a certain amount of heat is needed to raise the temperature of an object by 10 C (1 K), this same amount of heat will be given out if the object cools by 10 C.

Remember that a temperature difference of 1 K is the same as a temperature difference of 10 C.

*rq: pronounced “delta theta”
The symbol r is used in many contexts to symbolise “change”. In fact the expression dy/dx is shorthand for
ry/r x ; ‘a change in y divided by a change in x’. This corresponds to the slope of a line where y is on the vertical axis. The formula y2 – y1 / x2 –x1 is merely a more cumbersome way writing this same thing. Of course it’s easy to calculate the slope when you just have a straight line. But what about if instead of a line you have a curve, and you want to find the slope of the curve (at a specific point)?
This is where the genius of Newton came in. He invented ‘Differentiation’ and its associated rules to enable us to calculate this. Differentiation, together with its sister ‘Integration’ come together to form an area of mathematics called ‘Calculus’.
At approximately the same time as Newton was coming up with this, another mathematician called Leibtniz was discovering it independently, but with different notation. When Newton found out about this he accused Leibtniz of stealing his ideas and threw the mother of all sulks. To make things worse, it was Leibtniz’ who used the notation ry/r x. Newton’s was considered to be too cumbersome. You might still come across it in places. He used f’(x) and f’’(x) to signify first order and second order differentiation.

*Graph of Temperature versus Time for water: Latent Heat Curve
Explanation
If you've got a block of ice at –50 C and heat it up, you will notice that while it's melting the melted water will not rise above 00 C until all the ice has melted. The heat which is being added is not causing a rise in temperature – hence the term ‘latent heat’ (‘hidden heat’).
Only when all the ice has turned to water does the temperature begin to rise again.
Similarly when the water reaches boiling point at 1000 C, the water which turns to water vapour first will not rise above 1000 C until it's all water vapour.

Nobody has ever asked me why this should be the case, which is a small cause for concern, but just goes to show that we really are teaching students not to think for themselves.
Anyway, to make sense of the curve, I think it must mean that ice absorbs heats better than water, which would explain why all the ice turns to water before the water heats up, and similarly at the water/steam point.
Now this merely begs the follow up question; why does ice absorb heat more quickly than water?
This in turn brings us back to our definitions of heat capacity.
Why does one substance have a different specific heat capacity than another?
I guess it must mean that the forces between the water molecules in the ice stage are less than the forces between them in the water stage.
But isn't it interesting that we as physics teachers give the impression that what you read in the book is all there is to it, whereas in actual fact these questions only serve to open the door on a whole new and deeper level of understanding.
It's no wonder that students are walking away from physics in the classroom.
Or maybe it’s just me.

Oh by the way, all (and I mean all) textbooks which give this diagram conveniently omit to mention that it is next to impossible to achieve this in practice.. It assumes all energy goes into the water; that there is no loss of energy by conduction, convection or radiation; that water evaporates only when it is boiling, and that pressure is kept constant.

*Refrigerator
Did you know that if you leave a fridge open it will not cool down a room?
This is because all the heat it removes merely gets transferred to the back of the fridge where it gets pushed out into the room.

*Perspiration and Latent heat
The reason we perspire is to cool us down – everybody knows that, but how does it work?
It’s not obvious, but we are relatively large source of heat, and when a drop of water forms on our skin it can take heat from the skin and as a result heat up and then evaporate as it turns to a gas.
But because water has quite a high shc and lh, one drop can actually absorb a lot of heat.
For example one gram of sweat evaporating from your body removes 2,410 Joules of Heat energy.
So why don’t you catch a cold in a swimming pool’

While we’re at it, why does it seem so cold when you get out of a swimming pool?

Why might getting caught in a shower of rain result in you catching a cold, or even worse – pneumonia?

Put a dollop of perfume on your hand - what should you notice and why?

Dip a thermometer in (warm) perfume, or wrap an alcohol-soaked rag around a thermometer. What happens?
Why is water a very good substance for fire extinguishers?
Why is a steam burn more dangerous than a burn from boiling water, even when both are at the same temperature (1000 C)?

*Heat Transfer
Conduction
You get up for a pee in the middle of the night.
On your way to the bathroom you pass over different floors composed of (i) ceramic tiles, (ii) timber and (iii) woollen carpet. Now all three floors are at the same temperature (room temperature), so why do they seem to be at different temperatures?

Convection
Fill balloon with water, heat it first with a match, then a cigarette lighter. Amazingly the balloon does not burst.
Why?
Even though the plastic material the balloon is made from would not be considered a good conductor, it is very thin (the experiment works best when the balloon is full, causing the skin to be stretched) and heat is quickly transferred away from the point of contact due to convection. It is also helped by the relatively large specific heat capacity of water; it can take in a very large amount of heat before it gets very hot.
Eventually however the balloon does develop tiny holes and the water will flow out.
Demo is best done over a basin just in case there is a problem with the balloon.
But over a student’s head is much more fun.

Radiation
We have 18 foot ‘Solar Balloons’ which rise very nicely on a sunny day (there must be very little breeze). The black material absorbs heat and the air inside heats up, expands and because the system is now less dense than the surrounding air, up she goes!

A thermos flask uses the principles of conduction, convection and radiation to keep the liquid inside from cooling down (or indeed heating up)
Can you figure out the role played by each?

*U-Value
So why the letter ‘U’?
Apparently it’s short for the term ‘Unit Heat Loss Rate’.
It seems to have the opposite meaning to ‘tog value’ for fibres in that the greater the U-value the poorer an insulator it is.

Exam questions

Specific heat capacity of copper = 390 J kg–1 K–1; Specific heat capacity of water = 4200 J kg–1 K–1
Specific latent heat of fusion of ice is 3.3 × 105 J kg-1

[2003][2008 OL][2010 OL]

What is heat?

[2003 OL][2004 OL][2005 OL][2006 OL][2007 OL][2008 OL][2009]

Name two methods by which heat can be transferred.

[2004 OL]

What is meant by conduction?

[2010 OL]

Explain how heat is transferred in a solid.

[2004 OL][2010 OL]

Describe an experiment to show how different solids conduct heat at different rates.

[2004 OL]

Why are the pipes in the solar panel usually made from copper?

[2010 OL]

Explain the term ‘U-value’.

[2002 OL]

What is the effect of increasing the U-value of a structure?

[2004 OL][2010 OL]

The U-value of a house is a measure of the rate of heat loss to the surroundings.
Give two ways in which the U-value of a house can be reduced.

[2006 OL]

In an electric storage heater, bricks with a high specific heat capacity are heated overnight by passing an electric current through a heating coil in the bricks. The bricks are surrounded by insulation.
Why is insulation used to surround the bricks?

[2006 OL]

Name a material that could be used as insulation in a storage heater.

[2006 OL]

What is convection?

[2006 OL]

Describe an experiment to demonstrate convection in a liquid.

[2002 OL]

Why is the heating element of an electric kettle near the bottom?

[2006 OL]

Explain how the storage heater heats the air in a room.

[2004 OL]

Why does warm water rise to the top of the solar panel?

[2008]

An electric toaster heats bread by convection and radiation.
What is the difference between convection and radiation as a means of heat transfer?

[2004]

Why are the pipes in the solar panel usually painted black?

[2006][2004] [2002 OL][2008 OL]

Define specific heat capacity.

[2004]

Define specific latent heat.

[2004]

Storage heaters have a large heat capacity. Explain why.

[2007]

Why does the temperature of an athlete reduce when she perspires?

[2010]

Explain why snow is slow to melt as the day-time temperatures rises above 0 °C.

[2006 OL]
The total mass of the bricks in a storage heater is 80 kg and their specific heat capacity is 1500 J kg–1 K–1.

During a ten-hour period the temperature of the bricks rose from 15 oC to 300 oC.
Calculate the energy gained by the bricks.

Calculate the power of the heating coil.

[2009]

How much energy is required to raise the temperature of 500 litres of water from 20 0C to 50 0C?
(specific heat capacity of water = 4200 J kg–1 K–1; density of water = 1000 kg m–3; 1 litre = 10–3 m3)

[2002 OL]
An electric kettle contains 1.5 kg of water. The specific heat capacity of water is 4180 J kg-1 K-1.

Calculate the amount of energy required to raise the temperature of the water from 15 0C to 100 0C.

The kettle takes 4 minutes to heat the water from 15 0C to 100 0C. Calculate the power of the kettle.

(Assume all the energy supplied is used to heat the water).

[2006]
400 g of water at a temperature of 15 oC is placed in an electric kettle. The power rating of the kettle is 3.0 kW. Calculate the energy required to raise the temperature of the water to 100 oC.
Calculate the energy supplied by the kettle per second.
Calculate the least amount of time it would take to heat the water to 100 oC.
In reality, the time taken to heat the water will be greater. Explain why.

[2008 OL]

A saucepan containing 500 g of water at a temperature of 20 °C is left on a 2 kW ring of an electric cooker until it reaches a temperature of 100 °C.

Calculate the rise in temperature of the water.
Calculate the energy required to heat the water to 100 °C.
Calculate the amount of energy the ring supplies every second.
Calculate the time it will take to heat the water to 100 °C.

[2004]
500 g of water at a temperature of 15 0C is placed in a freezer.

The freezer has a power rating of 100 W and is 80% efficient.
Calculate the energy required to convert the water into ice at a temperature of –20 oC.

How much energy is removed every second from the air in the freezer?
How long will it take the water to reach a temperature of –20 oC?
Allowing a liquid to evaporate in a closed pipe inside the freezer cools the air in the freezer. The vapour is then pumped through the pipe to the outside of the freezer, where it condenses again.

Explain how this process cools the air in the freezer.

The freezer causes the room temperature to rise. Explain why.

[2009]

Read the following passage and answer the accompanying questions.
The sun is a major source of ‘green’ energy. In Ireland solar heating systems and geothermal systems are used to get energy from the sun.
There are two main types of solar heating systems, flat-plate collectors and vacuum-tube collectors.

A flat-plate collector is usually an aluminium box with a glass cover on top and a blackened plate on the bottom. A copper pipe is laid on the bottom of the box, like a hose on the ground; water is passed through the pipe and transfers the absorbed heat to the domestic hot water system.

In a vacuum-tube collector, each tube consists of an evacuated double-walled silvered glass tube in which there is a hollow copper pipe containing a liquid. The liquid inside the copper pipe is vaporised and expands into the heat tip. There the vapour liquefies and the latent heat released is transferred, using a heat exchanger, to the domestic hot water system. The condensed liquid returns to the copper pipe and the cycle is repeated.
In a geothermal heating system a heat pump is used to extract solar energy stored in the ground and transfer it to the domestic hot water system.

Why is the bottom of a flat-plate collector blackened?
The liquid in a vacuum-tube solar collector has a large specific latent heat of vaporisation. Explain why.
How is the sun’s energy trapped in a vacuum-tube solar collector?
Describe, in terms of heat transfer, the operation of a heat pump.
Give an advantage of a geothermal heating system over a solar heating system.

[2010 OL]

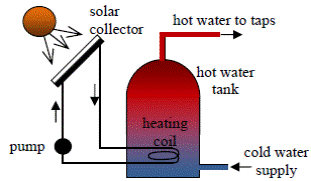
The diagram shows a solar heating system.

How is the sun’s energy transferred to the solar collector?
Why is the solar collector normally painted black?
How is the heat transferred from the solar panel to the hot water tank?
The heating coil for the hot water tank are placed at the bottom, explain why.
Give an advantage and a disadvantage of a solar heating system.

Mandatory Experiments

[2004 OL][2010 OL]

In a report of an experiment to measure the specific heat capacity of a substance (e.g. water or a metal), a student wrote the following.
“I assembled the apparatus needed for the experiment.
During the experiment I took a number of measurements of mass and temperature.
I used these measurements to calculate the specific heat capacity of the substance.”

Draw a labelled diagram of the apparatus used.
What measurements of mass did the student take during the experiment?
What temperature measurements did the student take during the experiment?
Give a formula used to calculate the specific heat capacity of the substance.
Give one precaution that the student took to get an accurate result.

[2009 OL]

A student carried out an experiment to measure the specific latent heat of fusion of ice.
The following is an extract from her report.
“In my experiment, I prepared ice which was at 0 0C and I added it to warm water in a calorimeter. I waited for all the ice to melt before taking more measurements.
I used my measurements to calculate the specific latent heat of fusion of ice.”

Draw a labelled diagram of the apparatus used in the experiment.
What measurements did the student take in the experiment?
How did the student prepare the ice for the experiment?
How did the student know the ice was at 0 0C?
Why did the student use warm water in the experiment?

In a report of an experiment to measure the specific latent heat of fusion of ice, a student wrote the following.
“Ice at 0 0C was added to water in a calorimeter.
When the ice had melted measurements were taken.
The specific latent heat of fusion of ice was then calculated.”

Draw a labelled diagram of the apparatus used.
What measurements did the student take before adding the ice to the water?
What did the student do with the ice before adding it to the water?
How did the student find the mass of the ice?
Give one precaution that the student took to get an accurate result.

[2008]

In an experiment to measure the specific latent heat of fusion of ice, warm water was placed in a copper calorimeter. Dried, melting ice was added to the warm water and the following data was recorded.
Mass of calorimeter 60.5 g
Mass of calorimeter + water 118.8 g
Temperature of warm water 30.5 oC
Mass of ice 15.1 g
Temperature of water after adding ice 10.2 oC

Explain why warm water was used.
Why was dried ice used?
Why was melting ice used?
Describe how the mass of the ice was found.
What should be the approximate room temperature to minimise experimental error?
Calculate the energy lost by the calorimeter and the warm water.
Calculate the specific latent heat of fusion of ice.

mass of calorimeter 55.7 g

mass of calorimeter + water 101.2 g

mass of copper + calorimeter + water 131.4 g

initial temperature of water 16.5 oC

temperature of hot copper 99.5 oC

final temperature of water 21.0 oC

[2007]

The specific heat capacity of water was found by adding hot copper to water in a copper calorimeter.
This was not the method most students would have used to carry out the experiment so there was much annoyance when it appeared on the paper. Nevertheless it does differentiate between those students who understand the underlying principles and those who have just learned off a formula.
The following data was recorded.

Describe how the copper was heated and how its temperature was measured.
Using the data, calculate the energy lost by the hot copper
Using the data, calculate the specific heat capacity of water.
Give two precautions that were taken to minimise heat loss to the surroundings.
Explain why adding a larger mass of copper would improve the accuracy of the experiment.

[2002]

In an experiment to measure the specific latent heat of fusion of ice, warm water was placed in an aluminium calorimeter. Crushed dried ice was added to the water.
The following results were obtained.
Mass of calorimeter.......................................= 77.2 g
Mass of water.................................................= 92.5 g
Initial temperature of water...........................= 29.4 0C
Temperature of ice ........................................= 0 0C
Mass of ice.....................................................= 19.2 g
Final temperature of water.............................= 13.2 0C
Room temperature was 21 0C.

What was the advantage of having the room temperature approximately halfway between the initial temperature of the water and the final temperature of the water?
Describe how the mass of the ice was found.
Calculate a value for the specific latent heat of fusion of ice
The accepted value for the specific latent heat of fusion of ice is 3.3 × 105 J kg-1; suggest two reasons why your answer is not this value.
[2005 OL]

In a report of an experiment to measure the specific latent heat of vaporisation of water, a student wrote the following.
“Steam at 100 oC was added to cold water in a calorimeter.
When the steam had condensed, measurements were taken.
The specific latent heat of vaporisation of water was then calculated.”

Draw a labelled diagram of the apparatus used.
List two measurements that the student took before adding the steam to the water.
How did the student find the mass of steam that was added to the water?
How did the student make sure that only steam, and not hot water, was added to the calorimeter?
Give one precaution that the student took to prevent heat loss from the calorimeter.

[2003]

In an experiment to measure the specific latent heat of vaporisation of water, cold water was placed in a copper calorimeter. Steam was passed into the cold water until a suitable rise in temperature was achieved.
The following results were obtained:
Mass of the calorimeter........................... = 73.4 g
Mass of cold water .................................. = 67.5 g
Initial temperature of water..................... = 10 °C
Temperature of the steam........................ = 100 °C
Mass of steam added ............................... = 1.1 g
Final temperature of water ...................... = 19 °C

Describe how the mass of the steam was found.
Using the data, calculate a value for the specific latent heat of vaporisation of water.
Why is the rise in temperature the least accurate value?
Give two ways of improving the accuracy of this value.

[2010]

In an experiment to measure the specific latent heat of vaporisation of water, a student used a copper calorimeter containing water and a sensitive thermometer. The water was cooled below room temperature before adding dry steam to it. The following measurements were recorded.
Mass of copper calorimeter = 34.6 g
Initial mass of calorimeter and water = 96.4 g
Mass of dry steam added = 1.2 g
Initial temperature of calorimeter and cooled water = 8.2 °C
Final temperature of calorimeter and water = 20.0 °C

How was the water cooled below room temperature?
How was the steam dried?
Describe how the mass of the steam was determined.
Why was a sensitive thermometer used?
Using the data, calculate the specific latent heat of vaporisation of water.

[2005]

In an experiment to measure the specific latent heat of vaporisation of water, cool water was placed in an insulated copper calorimeter. Dry steam was added to the calorimeter. The following data was recorded.
Mass of calorimeter = 50.5 g
Mass of calorimeter + water = 91.2 g
Initial temperature of water = 10 oC
Temperature of steam = 100 oC
Mass of calorimeter + water + steam = 92.3 g
Final temperature of water = 25 oC

Calculate a value for the specific latent heat of vaporisation of water.
Why was dry steam used?
How was the steam dried?
A thermometer with a low heat capacity was used to ensure accuracy. Explain why.

Exam solutions

Specific heat capacity of copper = 390 J kg–1 K–1; Specific heat capacity of water = 4200 J kg–1 K–1
Specific latent heat of fusion of ice is 3.3 × 105 J kg-1

Heat is a form of energy
Conduction, convection and radiation.
Conduction is the movement of heat energy through a substance by the passing on of molecular vibration from molecule to molecule, without any overall movement of the substance.

heat

Atoms are touching / in contact so the heat/energy gets transferred from one to the other by vibration (without the atoms moving along).
Apparatus: See diagram. 4 different metals arranged as shown. Stick an upright match into the pool of wax which is at the other end.

Procedure: Light a candle underneath the middle.
Observation: e.g. wax melts and the matches fall on different rods at different times.

It is a good heat conductor.
The U-value of a house is a measure of the rate of heat loss to the surroundings.
It means that the heat conductivity of the structure is increased.
Fibreglass in attic, insulation in cavity wall, double glazing, carpets
To prevent heat-loss.
Fibre glass / rockwool / cotton wool.
Convection is the transfer of heat through a fluid by means of circulating currents of fluid caused by the heat.
Apparatus: See diagram with container, water, dye, heat source labelled.

Procedure: add the dye to the liquid and heat.
Observation: convection current becomes visible.

Because hot water rises.
The heater heats the air which is beside it. This hot air then rises and is replaced by cold air. This process then gets repeated.
The water expands when heated and therefore has a lower density and gets replaced by water which has a higher density (cold water). This is convection.
Convection requires a medium, radiation does not.
Black is a good absorber of radiation.
The specific heat capacity of a substance is the heat energy needed to change one kilogram of the substance by one Kelvin.
The Specific Latent of a substance is the amount of heat energy need to change the state of 1 kg of the substance without a change in temperature.
They are heated only at night but must release energy slowly during the day.
As the water evaporates it takes heat energy from the body.
Latent heat of snow/ice (energy needed for change of state) is (very) large
Q = mcΔθ Þ Q = (80)(1500)(285) = 34 200 000 J = 34.2 MJ
P = W/ t Þ P = 34 200 000 / (10×60×60) = 950 W

Density = mass/volume Þ mass = (density)(volume) Þ m = (1000)(500 × 10–3) = 500 kg.

E = mcrq = (500)(4200)(30) = 6.3 × 107 J
(specific heat capacity of water = 4200 J kg–1 K–1; density of water = 1000 kg m–3; 1 litre = 10–3 m3)

Q = mcΔθ Þ Q = 1.5 × 4180 × 85 = 532 950 J.
P=W/t Þ P = 532 950/240 Þ P = 2221 W.
E = m c Δθ

E = (0.40)(4200)(85) = 1.428 × 105 J

3000 J per second = 3000 W
Time taken = 1.428 × 105/3000 = 47.6 s
Energy will be lost to the surroundings.

A saucepan containing 500 g of water at a temperature of 20 °C is left on a 2 kW ring of an electric cooker until it reaches a temperature of 100 °C.

100 – 20 = 80 °C
Q = m cΔθ = 0.5 × 4200 × 80 = 168 000 J
2 kW = 2,000 W = 2,000 J per second.
P = W/t Þ t = W/P Þ t = 168 000/2,000 = 84 secs.
Cooling from 15 0C to 0 0C: Q = mcΔθ = (0.5)(4200)(15) = 31500 J

Change of state: Q = ml = (0.5)(3.3 × 105) =165000 J
Cooling ice from 0 oC to -20 oC: Q = (0.5)(2100)(20) =21000 J
Total energy required = Qt = Q1 +Q2 +Q3 =217500 = 2.2 × 105 J

80% efficiency ⇒ 80 W ⇒ 80 J (per second)
Power = Q ÷ time

t = (217500 ÷ 80) = 2700 s

This change of state requires energy (latent heat) which is taken from inside the freezer and this lowers the temperature .
Condensation (vapour to liquid) releases latent heat

Dark surfaces are good absorbers of heat/energy/radiation
So that a lot of energy gets absorbed (and then released) per kg in the heat exchanger during a change of state.
Silvered walls prevent radiation and evacuated walls prevent conduction and convection
Energy is taken from one place (making it colder) by allowing the liquid to change state to a gas.

Then in another place the gas condenses to a liquid releasing the heat to another place making it hotter.

Geothermal system functions all the time whereas a solar heating system works only during sunshine.

Radiation / rays
(black surfaces are) better absorbers (of heat/radiation)
By the water flowing/pumped (through the collector and the heating coil).
Water is heated by convection / hot water rises, etc.
Reduces costs, unlimited supply, no pollution, etc.

Needs sun, requires a back-up, costly to install, etc.

Mandatory Experiments

See diagram.
Mass of calorimeter, mass of calorimeter + water,
Initial temperature of water, final temperature of water.
Energy supplied = (mcΔθ)cal + (mcΔθ)water where Δθ is the change in temperature and ccal is known.
GLagging, use sensitive thermometer, ensure that heating coil is completely immersed in the liquid, stir the liquid, large temperature change, etc.

See diagram
Mass of calorimeter

Mass of calorimeter and warm water
Mass of calorimeter and warm water and ice
Temperature of water before
Temperature of water and melted ice after

It was crushed and then dried.
By using melting ice.
So that the heat lost to the environment when the system is above room temperature is balanced by the heat taken in from the environment when the system is below room temperature.

See diagram
Mass of calorimeter, mass of water, mass of calorimeter + water, mass of ice, temperature of water
The ice was crushed and dried.
(mass of calorimeter + water + ice) – (mass of calorimeter + water)
Insulation, crush, dry, repeat and take average, use lots of ice, transfer ice quickly.

To speed up the melting of the ice / in order to melt a larger mass of ice / (concept of) balancing energy losses before and after the experiment.
To remove any water/melted ice // melted ice would have already gained latent heat //so that only ice is added // so that no water is added
Melting ice is at 0 oC.
Final mass of calorimeter + contents minus mass of calorimeter + water.
20 0C / midway between initial and final temperatures (of the water in the calorimeter)
{energy lost = } (mcΔθ )cal + (mcΔθ )warm water

= (0.0605)(390)(20.3) + (0.0583)(4200)(20.3)
= 5449.6365 / 5449.6 J

{Energy gained by ice and by melted ice =}

(ml)ice + (mcΔθ )melted ice / (0.0151)l + (0.0151)(4200)(10.2) / 0.0151 l + 646.884
(equate:) 0.0151 l + 646.884 = 5449.6365
l = 3.181 × 105 ≈ 3.2 × 105 J kg–1

It was heated using a hot-plate and temperature was measured using a thermometer.
E = m c Δθ

E = (3.02 × 10-2)(390)(78.5) = 924.6 J

Heat lost by hot copper = heat gained by calorimeter + water

924.57 = (0.0557)(390)(4.5) + (0.0455)(cw)(4.5)
Þ 924.57 = 97.75 + 0.2048 cw
cw = 4.04 ×103 J kg-1 K-1

Insulate calorimeter /use lid /transfer copper pieces quickly / use cold water (below room temperature) / polish calorimeter / low heat capacity thermometer
A larger mass of copper would result in a larger temperature change and therefore smaller percentage error.

Heat lost to surroundings when the system is above room temperature would cancel out the heat taken in from the surroundings when the system was below room temperature.
Final mass (of calorimeter + water + ice) - initial mass (of calorimeter + water)
mcΔθAl + mcΔθwater = mlice +mcΔθmelted ice

Fall in temperature = 16.2 oC
Ans = 3.2 × 105 J kg-1

Thermometer not sensitive enough, lack of insulation, lack of stirring, heat loss/gain to surroundings, too long for ice to melt, inside of calorimeter tarnished, splashing, heat capacity of thermometer

heat

See diagram.
Mass of calorimeter, mass of water, mass of calorimeter + water, initial temperature of water, initial temperature of steam.
Final mass of water + calorimeter minus initial mass of water + calorimeter.
Allow steam to flow for some time before inserting it into water, slope delivery tube back to steam generator, use a steam trap.
Lagging, insulation, lid, carry out measurements quickly.

Final mass of (calorimeter + water + condensed steam) – Initial mass of (calorimeter + water)
(ml) steam + (mc∆ϑ) steam = (mc∆ϑ) water + (mc∆ϑ) cal

∆ϑwater = 90C, ∆ϑcal= 90C
∆ϑ) steam = 810C
Answer = 2.2 × 106 J kg-1

Read only to one significant figure {the concept of significant figures is not on the syllabus and shouldn’t have got asked. It hasn’t appeared since.]
Use a digital thermometer, use more steam, use less water, insulation, cover, stirring, steam trap

Ice was added to the water / the water was taken from fridge
By using a steam trap (or ensure that the delivery tube is sloped upwards)
Final mass of calorimeter plus contents – initial mass of calorimeter and contents
For greater accuracy / to reduce (%) error / more significant figures / e.g. to read to 0.1 oC
ms = 1.2×10-3 kg

mw = 6.18 × 10-2 kg
Δθs = 80 (K) and
Δθw (= Δθcu) = 11.8 (K)
[heat lost by steam = heat gained by water and calorimeter]
(ml)s + (mcΔθ )s = (mcΔθ )w + (mcΔθ )cu
(1.2×10-3)l + (1.2×10-3)(4180)(80) = (6.18 × 10-2)(4180)(11.8) + (3.46 × 10-2)(11.8)(390)
(1.2×10-3)l + 401.3 = 3048.2 + 159.2
l = 2.34 × 106 J Kg-1

mslw + mscwΔθs = mwcwΔθw+ mcccΔθc

Δθs = 75 0C and Δθw (= Δθc) = 15 0C
(0.0011) lw + (0.0011)(4200)(75) = (0.0407)(4200)(15) + (0.0505)(390)(15)
[(0.0011) lw + 346.5 = 2564.1 + 295.425]
lw = 2.28 × 106 J kg-1

Calculations assume that only steam is added, not water.
Use a steam trap / insulated delivery tube / sloped delivery tube / allow steam to issue freely initially
It absorbs little heat from system in calorimeter and calculations assume that no energy is transferred to the thermometer.

Source : http://www.thephysicsteacher.ie/LC%20Physics/Student%20Notes/15.%20Heat.doc

Web site link: http://www.thephysicsteacher.ie

Author : not indicated on the source document of the above text

If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.

Quantity of Heat and Heat Transfer

Main page

Alimentation - nutrition

Animals

Architecture

Art

Astrology, esoteric, parapsychology and fantasy

Astronomy

Biology and genetics

Botany and agriculture

Chemistry

Courses, training, guides, handbooks and tips

Culture General and actuality

Dermatology, health and wellness

Dictionaries and glossaries

Economics and finance

Education and pediatrics

Engineering and technology

English grammar and anthology

Fashion and show business

Fitness

Food, recipes and drink

Games, play space

Geography, geology and environment

History

Informatics and computer world

Jobs world

Languages

Leisure and DIY do it yourself

Lessons for students

Literature, biographies and journalism

Mathematics, geometry and statistical

Medicine

Music

Notes and concept maps

Philosophy

Photography and images - pictures

Physics

Physiology

Psychology and psychoanalysis

Quiz questions and answers

Religions

Rights law and political science

Science

Sociology and cultural anthropology

Sport

Summaries and reviews

Television, film - movies and comics

Theater and communications

Theses, themes and dissertations

Travel and tourist guides

Useful documents and tables

Utility, calculators and converters

Weather and meteorology

Quantity of Heat and Heat Transfer

This is the right place where find the answers to your questions like :

Who ? What ? When ? Where ? Why ? Which ? How ? What does Quantity of Heat and Heat Transfer mean ? Which is the meaning of Quantity of Heat and Heat Transfer?

Quantity of Heat and Heat Transfer physics notes

Alanpedia.com from 1998 year by year new sites and innovations

Main page - Disclaimer - Contact us