Solving physics problems
Solving physics problems
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Solving physics problems
Introduction to Problem Solving:
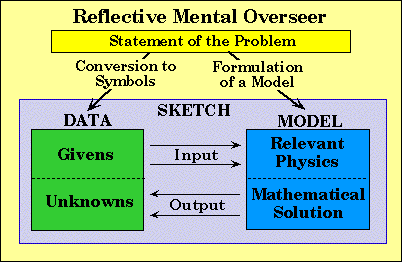
Reflective Mental Overseer
(The Thinker of Your Thoughts)
Many of the steps we use to solve a problem we carry out unconsciously. They are a part of the way we think, and we just seem to know how to do them without thinking about how we go about doing them. This is just like walking were once learned, we no longer need to be consciously aware of the multitude of operations taking place when we decide to walk from one class to another.
It seems that once we have learned the details of some process through conscious effort, this process is still available to us just by evoking the process itself: "walk to the door and open it" or "plug this value into that equation".
When we encounter novel situations in which our current way of thinking does not work, it is important to take conscious control of our thinking -- to begin thinking about our thinking and about our problem-solving process. One way to gain some insight is to have the thinker of your thought ask some explicit questions about your problem-solving activities.
A few examples are:
What quantities are given in the statement of the question? Do I have them all?
Is the quantity that I just calculated the actually quantity requested by the problem?
What physical situation is described in this problem?
How do I turn the information requested into a mathematical statement?
What is implied by this question, but is not explicitly stated in the question itself?
What principles of physics do I need to understand in order to figure out how to obtain an equation that relates the knowns to the unknowns?
Is what I am doing making sense? Is my answer reasonable?
What makes me believe that the equation I am using really applies to this problem?
What does this symbol mean? Does it mean what I think it means?
From what frame of reference shall I choose to observe the action described?
What if ..., what would that imply in this problem?
What would I have needed to understand that would have allowed me to figure out how to solve the problem myself?
By consciously becoming aware of these types of questions before you encounter some difficulty, it is my belief that they will become a part of your intuitive, spontaneous problem-solving ability in the future
Solving Physics Problems
When solving a problem ask yourself to consider the following:
- Physical Process depicted in the problem.
- Information Given and implied in the problem.
- Unknown Information requested in the problem.
- Frame of Reference from which the problem will be analyzed.
- Relevant Physics that applies to the problem.
- Mathematical Methods you will used to find the unknowns.
- Scrutinizing your Answers to determine their validity.
When you encounter difficulties it is very useful to reflect on your own problem-solving process. The areas above are the most important areas that you will need to consider.
When analyzing a problem, the exact order of the areas above is inconsequential. You may cycle around or go back and forth between these areas several times. Starting with an area that you feel the most confident usually works the best. When you have exhausted your understanding of one part, it is time to move on to another area. Figuring out something in one part can often help you figure out something else in other part which in turn can help you figure out another piece of the puzzle.
1. Sketching The Physical Process
Reflective Mental Overseer Question:
- What physical situation or process is depicted in the problem ?
Examples:
A boy applies a torque to open a door.
Two blocks collide and stick together.
Water flows through a constriction in a pipe.
Gas is compressed in a cylinder.
Action:
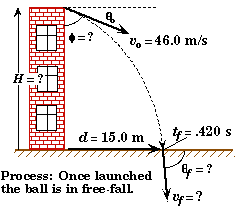- Make a schematic sketch of the process described in the problem.
Example:
A ball is thrown at an unknown downwards angle from the top of a building at a speed of 46.0 m/s. The ball is observed to hit the ground 15.0 m from the base of the building, .420 seconds after it is launched.
(A) At what angle relative to the face of the building was the ball thrown ?
(B) How high is the building ?
(C) At what speed and direction did the ball hit the ground ?
Comment:
- "One sketch is worth a thousand words." Making a sketch is one of the most important organizational aids you can use to cast the verbal statement of a problem into a visual structure that can summarize all the relevant information needed to solve the problem.
- Sketches do not have to be elaborate pictures. Objects only need to be simple symbolic representations - the simpler the better. My sketches are often too elaborate because I have access to a computer drawing program. In a "real" problem, I would have represented the building by a simple rectangle.
2. The Information Given or Implied
Reflective Mental Overseer Questions:
- What numerical values are stated explicitly in the body of the question ?
Example:
"Starting from rest an object..." is a explicit statement that the initial velocity of the object is zero. Expressed mathematically, vo = 0.
- What information is implied by this type of question but is not explicitly stated ?
Example::
In free-fall problems, it is often assumed that the effects of air resistance are small and can be neglected. Expressed mathematically, this means that the acceleration of the object is equal to g = 9.80 m/s2, downwards.
- How will I label the quantities given ?
Action:
Select labels for the quantities given and write down their values. These labels can be any personal tags you choose.
Examples: vo= 12.0 m/s, EA= 145 kJ, mboy= 34.0 kg
When applicable, place the knowns (symbol = value) on the sketch of the process at the appropriate location.
Example:
If a station wagon travels at a speed of 25.0 m/s, how far can it travel in 11.0 minutes ?
Although not explicitly stated, it is reasonable to assume that the automobile is moving at a constant speed in this problem.
Comment:
- Except in the simplest of problems, the personal labels you use will not necessarly be the same as the generic labels used in the equations found in the textbook.
- It is important to keep track of the meaning of each symbol you use, how it is connected to those used in the textbook, and how it is connected with the physical quantities described in the problem.
3. The Information Requested
Reflective Mental Overseer Questions:
- What physical quantities' values are requested in the problem ?
- How do I turn the information requested into a mathematical statement ?
- How will I label the unknowns requested ?
Actions:
- Select symbols for all unknowns.
Examples: vf, t2, KEtop
- Place a question mark after each to indicate that its value is requested.
Examples: vf = ?, t2 = ?, KEtop = ?
- When applicable, place the unknowns ("symbol" = ?) on the sketch of the process at the appropriate location.
Example:
A car traveling at 60.0 km/hr brakes to a halt in 140 m at a uniform rate.
(A) What was the car's acceleration while braking ?
(B) How long did it take the car to come to a stop ?
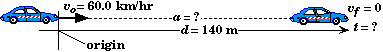
Comments:
- There may be other quantities that are not requested that may need to be both symbolized and found before the requested unknown can be found.
- The symbols with which you tag an unknown may be personal to you. In that case you will need to link your personal symbols with those used in the equations in the textbook or class notes, the generic equations.
- When examining an equation there is no way for you to see which symbols are knowns and which are unknowns. It takes practice to mentally keep track of those symbols that just represent some number, the knowns, and those symbols which are important to focus on, the unknowns.
- It often helps to restate the problem in terms of the symbols you have chosen for the givens and the unknowns. In the example problems in here you will see this done at the beginning of each example problem solution. For example: "Find Fapp given ab = 4.00 m/s2 and mb = 3.00 kg." is equivalent to "If a 3.00 kg block is accelerated at a uniform acceleration of 4.00 m/s2 on a frictionless surface, what force must be applied to the block ?"
5. The Frame of Reference
Reflective Mental Overseer Questions:
- From what point of view will I choose to observe the action described in this problem ?
- Where will I place the origin and when will I start the clock running ?
Actions:
- Designate the location of the frame of reference in some manner like placing a "+" at the origin of the coordinate system on your sketch. This determines the value of xo. Normally xo = 0 if you place the origin at the initial location of an object. When two or more objects are present, the initial position of all the objects cannot be zero unless they are at the same point initially.
- Choose when you will start the clock. This determines the value of to. Normally to= 0 if you start the clock at the start of some action.
- Choose which direction will be positive and which direction will be negative. Normally, directions to the right are taken to be positive as are directions upwards.
- For rotational problems choose either clockwise or counterclockwise as the positive rotational direction.
Comment:
- The structural form of the equations that you generate to solve a problem will be different for different locations of the origin.
- Some frames of reference produce easier equations to solve.
- Switching your frame of reference in the middle of a solution will almost always lead to disaster unless you are consciously aware that you are doing so.
- The generic equations in the book generally apply to a particular frame of reference which you will need to modify to fit your selected point of reference.
- A frame of reference could also be moving.
6. The Relevant Physics
Reflective Mental Overseer Questions:
- What principles, laws, or concepts apply to this type of problem ?
- What do I need to know about this principle, law, or concept in order to figure out how to obtain an equation(s) that relates the unknowns to the knowns?
- What specific conditions are stated or implied about the quantities involved in this type of problem ?
- To which object (or group of objects) will I apply the laws of physics that are relevant ? Equivalently, what system shall I choose to focus my attention upon ?
- What generic equation (or set of equations) goes with the principle or law that is relevant to this problem?
What principles, laws, or concepts apply to this type of problem ?
Examples:
Is energy conserved in this problem ?
Does this problem involve vectors ?
Are Newton's laws of motion relevant to this problem ? If so, which one ?
What do I need to know about this principle, law, or concept in order to figure out how to obtain an equation(s) that relates the unknowns to the knowns ?
Examples:
If this problem involves the conservation of moment, do I need to review or investigate that principle more before I attack this problem ?
If this problem involves vectors, do I know how to manipulate vectors well enough to solve this problem ? If I get stuck maybe the concept of vectors is an area that I should review.
How have I applied this principle or law to problems in the past ? If I have never applied this principle before, maybe I should look at an example problem to see how the principle is applied, or maybe I should study the topic first.
What specific conditions are stated or implied about the quantities involved in this type of problem ?
Examples:
If there is a force involved, is that force constant or variable ? In which direction and on what object is it acting ?
Are frictional forces important in this problem ?
Is the object moving at a constant speed or a constant acceleration ?
To which object (or group of objects) will I apply the laws of physics that are relevant ? Equivalently, what system shall I choose to focus my attention upon ?
Examples:
If two blocks are connected by a rope, to which block shall I apply Newton's Second Law ? The first block or the second block, or maybe I should consider both blocks together as a single system. What about the rope, is that a system I should also consider ?
What generic equation (or set of equations) goes with the principle or law that is relevant to this problem?
Examples:
If the net force on a body is stated to be constant, then its accelerations must also be constant, and therefore the kinematic equations for constant acceleration must apply to the body in this problem.
Actions:
- Pick out a body to be the center of focus and concentrate on writing down the formulas as they apply to that body. Repeat this process if there are more than two objects involved.
- It is also possible to select a compound body to which a principle can be applied. The laws of physics work equally as well for a system of objects as they do for a single object.
- Express the principles, laws, or concepts as mathematical equations using the labels you selected for the knowns and unknowns.
Examples:
vf = acar t + vo, Fnet = mg - Fdrag, PEtop = KEbottom
Comments:
- There must be at least as many equations as there are unknowns. If you don't have enough equations then maybe there is some additional principle that you have overlooked.
- When studying an example problem focus on how the principle is applied to the question to generate a formula that solves the problem, and not on the specific steps. There are many ways to generate a final formula that will work.
- Do not expect the equations you generate (that apply to a specific problem) to look like the generic equations found in a textbook. Only in the simplest problems will the equations look the same.
- Even for similar type of problems that employs the same physics principle, the final solution-equation, the bottom line equation , may not look the same. Do not be misled into believing that the bottom line equation you used the last time you solved a problem of this type will be the same this time. What will be the same is the starting principle.
- Given your frame of reference and your personal labels, the resulting equations you come up with may look completely different from that of another student's equations. Both could be equally correct!
6. The Mathematical Solution
Reflective Mental Overseer Questions:
- What method will I use to solve the relevant physics equations for the unknowns ?
Purely Numerical Approach
Purely Symbolic Approach
Combined Numerical and Symbolic Approach
Computational Methods
Graphing Approach
Purely Numerical Approach
Action:
- Substitute the numerical values of all the known quantities into the relevant physics equations first, and then solve the resulting equations for any unknowns. It is advisable to convert the knowns into SI units before you substitute them into the relevant physics equations or else your resulting answer will not be in the units you expect.
Comments:
- The advantage of this method is that it is usually faster because it reduces complicated equations to simpler equations that can be more easily manipulated. It is also easier to see what quantities are unknown.
- The disadvantage of this method is that it is harder to both locate and correct any errors.
- Once you have solved a problem using numbers, you have an opportunity to go back and retrace your steps using symbols.
Purely Symbolic Approach
Action:
- Leave all knowns as symbols and solve for any unknowns as an equation in which the "unknown = expression of the knowns", one equation for each unknown. Then substitute the values of the knowns into the resulting the bottom line equation to determine the value of an unknown.
Comments:
- The advantage of this method is that it is easier to retrace the logic of the steps you used to solve the problem.
- Once a symbolic solution is determined, you do not need to resolve the problem for a change in the input values. You only need to substitute the new values into the final equation.
- Symbols are easier to write down and manipulate than numbers because they take less strokes to write down and are smaller in size than the numbers they represent.
Combined Numerical and Symbolic Method
Rather than use either a purely numerical approach or purely symbolic approach exclusively, it is often better to use a combination of the two processes.
Action:
- Focus on some important quantities whose values are unknown but would be useful to know, quantities that you can see how to find. Solve for them symbolically and then determine their numerical values. Then use these as new knowns to reformulate the problem into a new problem requesting the same unknowns but with more givens, namely the values you just determined.
Comments:
- The advantage of this approach is that you break the problem down into smaller chunks which can be more easily manipulated.
- Another advantage is that you get to see the numerical values of certain intermediate quantities. Many times you can tell if their values seem reasonable.
Computational Solutions
Another method is to use a computer to find an approximate solution. The exact procedure varies from language to language. The general approach is to first enter the relevant physics equation symbolically. Next enter the values of the known variables in that equation. Have the computer repeatedly iterate successive values for the independent variable to see how the system evolves.
Comments:
- One advantage is that this method is fast once you have learned how write good code.
- There are some problems that cannot easily be solved symbolically, or even solved at all symbolically.
- The disadvantage of this method is that if you make an error, you will not know it unless your answer looks unreasonable. For example, if you do not enter all the known values in SI units, then your computer will give you a number but it will not be dimensionally correct.
- There are disadvantages associated with the algorithms that your computer uses to solve the equation for the unknown. For example, the equation may have more than one solution and the solution your computer returns may not be the one you are seeking.
- Another disadvantage is that you lose touch with the problem-solving process. If you do not practice solving equations, then it becomes much harder to manipulate the relevant generic equations to generate an equation that you can put into your calculator to solve in the first place.
- This is a good method to use to double-check a symbolic solution.
Using a Graphing Calculator
Often it useful to plot the relevant physics equation(s) on a graphing calculator. Many times this can be done before manipulating any of the equations first. After plotting the equations one can sometimes just look at the graph and "visually figure out" the answer.
Example:
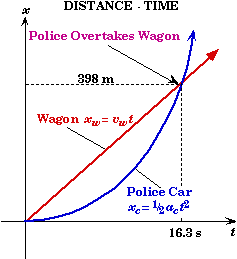
A speeding station wagon moving at a constant speed of 88.0 km/hr passes a parked police car. If the police car starts accelerating uniformly at 3.00 m/s2 from the moment the wagon passes the police car, how long will it take the police car to catch the station wagon ?
Plotting both the distance traveled by the station wagon and the distance traveled by police car on the same graph, we can see that where the two curves cross is the point where the police car catches up with the wagon. From the graph, we could also find the distance and the time it took for the police car to catch the wagon. Note that the graph on the right is only a schematic representation of what the plot would actually look like on your calculator. |
|
Comments:
- The visual display of a graph is extremely helpful in seeing what is taking place with the variables in a problem.
- When I get stuck in solving a problem, I will often plot up some of the relations that I believe are true. Seeing the graph, I can often tell if I am on the right track. If I am on the right track the structure of the graph will sometimes give me new insight into how to solve for a requested unknown.
7. Scrutinizing Your Results
Although this may look like the last step in solving a problem, it is useful to consider the following throughout your problem solving process.
Reflective Mental Overseer Questions:
- Do the signs of the quantities found make sense ?
- Do the magnitudes of the quantities found seem reasonable ?
- Are the units of the quantities found correct ?
- How can I check my answers mathematically ?
Do the signs of the quantities found make sense ?
Trouble-Shooting Actions:
- Go back and examine your choice of which directions will be positive and negative when you set up the frame of reference from which you observed the action of the problem.
- Examine the values you have written down for the givens to see if these values are consistent with your choice of positive and negative.
- Next examine the equations you are using to solve the problem. Are each of the terms in an equation consistent with your choice of what will be positive and what will be negative ?
Comments:
- Keeping the signs correct is one of the more difficult tasks that you will encounter in solving a problem. Part of the difficulty arises from the fact that there is no preferred direction which "Mother Nature" dictates as being positive or negative. It is up to you to choose which direction is positive. Depending upon the complexion of the problem, you may choose up to be positive in one problem and down in the next. This is perfectly acceptable. Experienced physicists usually choose the direction that will make the problem simplest to analyze. If an object's motion is always to the left, then choosing the left direction to be positive will make the equations of motion easier to analyze, rather than the normal convention of the right direction being positive.
- The generic equations of motion usually choose some direction as being positive. If your choice is different, then you will need to modify the generic equations to reflect your choice.
- Another situation that will cause the sign of some quantities to be off is your choice of the frame of reference. For example, say you have a hot block in contact with a cold block and want to analyze the heat flow between the two. From the hot block's perspective, the heat flows out of the hot block, which would be a negative loss. Alternatively, the cold block would see the heat flow as a positive energy gain.
Do the magnitudes of the quantities found seem reasonable ?
Trouble-Shooting Actions:
- Compare the value of the quantity found with the range of values of that quantity in situations where you have some prior knowledge. This requires experience and is not easy to do when you are first learning a new concept.
Comments:
- Learning the size quantities in different situations is not usually emphasized in most textbooks because of the time it would take to explore the use of that quantity over a large range of conditions. Sometimes textbooks will have a table of the values associated with different physical situations which can be useful.
- Every time you successfully solve a problem, it gives you some familiarity with the size of the quantities in that problem under the conditions stated in the problem. This awareness can be useful when solving future problems.
Are the units of the quantities found correct ?
Trouble-Shooting Actions:
- In addition to a quantity's numerical value, it is often useful to carry the units of each quantity you insert into an equation along with the numerical value to see if the resulting units at the end of the calculation are the same as the units of the quantity you set out to find.
Comments:
- If the final units do not match, then it means that either (a) you have made some mathematical error in manipulating the equation you are solving, or (b) that you have started with an incorrect equation to solve in the first place. This gives you two directions to explore: (a) going back through the mathematical steps of your solution to see if you can find any mistakes or (b) going back to the starting principles you employed to solve the problem that generated the equation you were using.
- A useful time-saving, work-a-round, is to make sure that the units (of the givens) are always converted into SI units before you begin substituting them into any equation you use. If the equation you are using is correct and you do not make any math errors in solving the equation, then you can rest assured that the final answer has the SI units of the quantity you sought. This method is helpful on an exam when time is short.
Is the quantity I found, the quantity requested in the problem ?
Trouble-Shooting Actions:
- It useful to pause at the end of a calculation and re-read the problem to see if what you just calculated is the same as the quantity requested.
- There are two levels on which you can check your answer:
(a) every quantity requested represents some type of physical quantity like time, energy, angular momentum, current, etc. The first thing to examine is to see if your answer represents the same type of physical quantity. If the problem calls for a speed then you should have found a quantity which is a speed.
(b) If your answer does represent the correct type of physical quantity, check to see if it is the actual value requested or if it is the value of some other related quantity. For example, there is an object's initial value, final value, average value, or change in velocity. All represent velocities but they are not the same. Moreover, there could be more that one object involved so you may need to make sure you have found the velocity of the correct object. You could also be requested to find the velocity of approach of the two objects, which is a velocity but again different from the other velocities mentioned
Comments:
- If the quantity you just found does not have the same units as the physical quantity requested, then you know you have either made a mistake in your calculation or you have a quantity -- whose value may be correct -- but it is not the one requested.
How can I check my answers mathematically ?
Trouble-Shooting Actions:
- To see if your answer is consistent with the information given, use your answer as a new "given-value" and place it into some related equation. Then check to see if it produces values that are identical with the original givens.
- A better, but longer method is to solve the problem using a different approach. There are usually many ways to solve the same problem. If you get the same answer using a different approach or a different equation, then there is a good chance that your answer is correct.
Comments:
- If you place your answer back into the equation which you were using to solve the problem and it gives the correct given values, then this does not necessarily mean that you have found the correct answer. It only means that you have solved the equations correctly. If the equation you started with is incorrect, then solving it correctly will not produce the correct answer to the quantity requested.
- Using a different method to solve a problem is a good way to help you build a conceptual model of the physics involved. When you approach something from a different angle, you will almost always learn something new that will help bind your understanding together into a bigger picture -- a more inclusive conceptual framework.
Summary: Typical Approach in Solving a Problem
The general approach that I use in solving a complex problem involves the steps below when all goes well. When the problem is simple, I am sometimes able to carry out all the steps at once. When I am struggling with a solution, I will generally focus on each step more carefully. Depending upon what catches my eye when I read and re-read the problem, I often change the order I use to analyze the problem. I focus on what I am the most certain about first.
- Read the problem to determine what physical process the problem is describing and make a preliminary guess as to what type of physics principles are involved.
- Make a simple sketch of the process and choose a possible frame of reference.
- Read the problem again to determine what information is explicitly stated.
- Select personal labels to tag the quantities given and add them to the sketch.
- Read the problem again to determine the information requested and tag any unknowns with labels. Add these labels to the sketch.
- Consider what information is probably implied but is not explicitly stated in the problem.
- If necessary, re-read the problem focusing on what law or principle of physics applies to the process taking place in the problem. If the physics involved is new, then I might review the topic material to expand my understanding of the principle to apply.
- Use the generic equations that are relevant and translate them into a set of equations using my personal labels, the information given, and the frame of reference chosen.
- Next apply some mathematical method to generate a bottom-line equation.
- For a symbolic solution, substitute the knowns into the bottom-line equation to determine the unknown requested.
- Finally examine my resulting answers to see if they seem reasonable.
Comments:
When you have found the correct answer (or what you believe is the correct answer) know that you now have a prime opportunity to expand your understanding of the physics underlying the problem. Now is not the time to stop, but to double-check your understanding by asking "what if" questions and exploring where they lead. Once you have a base of understanding connected with some physical process, it is a lot easier to broaden that base than to jump to the next problem and start all over again.
You will also learn a lot by trying to solve the problem using a different approach from a different perspective. There are usually many ways to solve a problem.
The danger of quitting once you find the answer is that it is easy to become imprinted into believing that the method you just used is "the way" one solves this type of problem. Change one tiny thing in a problem and the specific equation and steps needed to find the same variable can be entirely different. What will be the same is the relevant physics and the associated generic equations with which you start.
Generic Equations
The mathematical expression of some law or principle of physics is usually stated for the most general situation conceivable. These equations are typically found highlighted in the textbook or in the summary at the end of a chapter. Because they are so general, they are directly applicable to only very simple problems (which pertain to the relevant physics that produced those generic equations).
Real problems almost always involve more complex applications of the generic equations. As a result, the symbolic labels of these generic equations cannot be mapped onto the variables in a one-to-one fashion. This means that you will have to generate your own personal labels for the knowns and unknowns in a problem, and then map them onto the generic equations.
The generic equations are templates that can be applied to different parts of a problem. Each variable in a generic equation is a pointer to a concept. It is not the variable itself -- as a symbol -- that is important, but the concept that it signifies. You could use any symbol to represent the concept. The meaning of any symbol you see is not fixed in stone and can vary from problem to problem. What is fixed is the concept which the symbol tags. To be successful in solving problems, you will need to be consciously aware of the concept to which a symbol points.
"When does Friday come before Thursday this week?"
Answer: When you look them up in a dictionary.
This is an example of a joke that plays on the difference between the symbols "Friday" and "Thursday" which point to days of the week, and the symbols "Friday" and "Thursday" taken as a collection of letters. Taken as a collection of letters alone the answer is perfectly correct, but it is not correct for the meaning of the words/symbols which represent a day of the week.
The Bottom Line Equation
The bottom line in any symbolic solution is to arrive at an equation that looks like
unknown = expression of the knowns
From this point on, all one needs to do is "plug and grind". Any good calculator will carry out this step. This step employs the ability to use a calculator, and does not require understanding of the physics involved. The physics is in ascertaining the bottom-line equation, and not in evaluating it.
Do not be fooled into thinking that the bottom-line equation is the starting point in solving a problem.
It is with the fundamental generic equations (that apply to the problem) with which one should start each solution. Only when a problem is relatively simple will the bottom-line equation be identical to the generic equations in the textbook.
Figuring out what laws apply and how to express them mathematically is at the heart of the physics, and not the mechanical steps used to solve the equations.
Source: http://physics.mtsac.edu/4A/4A%20Text/SolvingPhysicsProblems.doc
Web site link: http://physics.mtsac.edu/
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
How to Solve Physics Problems
Below are a few guidelines about how to go about solving a physics problem. These guidelines have been proven to be used by many “masters” in the field and are helpful to solving lots of word problems. The best way to become a “master” problem solver is do what masters do.
- What are they talking about? The first step in the problem is determining what type of problem are they asking you, is it about buoyancy, motion, forces? Begin by reading the problem thoroughly and then labeling the problem as something that you think the problem is about.
- Draw a Picture. A picture can be worth a thousand words. The picture does not have to be perfect or nice but some pictorial representation of the word problem is always helpful especially for multiple step problems. A picture could also be a graph.
- Declare your variables. Now is the time to start writing down what you are given. Each number should be paired with a unit and given a variable it will represent. This can be done on your picture, or below your picture. The key is organizing it so that it is easy to understand and read.
- Begin Calculations. You can not begin calculations before you know what the problem is about and what variables you have. Now using what you have just done, look over your given variables, your picture, and the type of problem you said it was and try to find an equation which seems to best fit what you are given. Do not be afraid of writing down the wrong equation, this is a work in progress and often you may need several equations and not just one to finish the problem.
- Substitution. Now is the time you start plugging in your variables and manipulating the equations to find your answer(s).
- Check your answer(s). Does the answer seem to make sense with what you know about the world and how it behaves? Does it have the right units? If not go back to rereading the problem to see if there was something you missed, mislabeled, or forgot to include in your picture and begin again.
Source: http://www.sunydutchess.edu/mathlab/assets/How_to_Solve_Physics_Problems.doc
Web site link: http://www.sunydutchess.edu/
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Solving physics problems
Solving physics problems
Solving physics problems
how to solve physics problems
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Solving physics problems mean ? Which is the meaning of Solving physics problems?
Solving physics problems physics notes
how to solve physics problems
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us