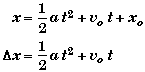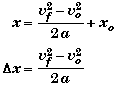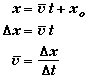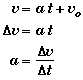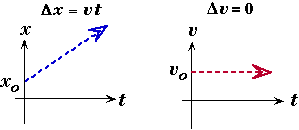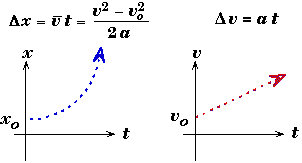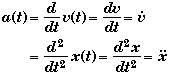Kinematics notes
Kinematics notes
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Kinematics notes
Introduction to Kinematics:
You have already completed a trigonometry based physics course. You know how to solve one-dimensional kinematics problems with constant acceleration. The purpose of this chapter is to introduce you to more sophisticated problem solving techniques and introduce several new concepts that will be used throughout the course. This material emphasizes using solved example problems to introduce new ideas. In the following problem, notice how the steps developed in the problem solving section are used.
Smoking Driver
A car is traveling at 120 km/hr due East on a flat road. |
|
How far does the car travel during a 3.50 second interval in which the driver looks away from the road to tune the radio or to light a cigarette ? |
|
At this speed how long will it take the car to travel a quarter of a mile ?
|
|

Information Given and Labels:
vc |
= 120 km/hr |
(Speed of the car) |
t |
= 3.50 s |
(Time the driver is distracted, part A) |
d |
=1/4 mi |
(Distance traveled, part B) |
Conversion of km/hr to the SI units of m/s.
![]()
Note that many books will put conversion of units in some table as 1 km/hr = .277 m/s or as 1 km/hr = .278 m/s. Both are only correct to 3 significant figures and can produce converted numbers in which the third significant figure is off.
For this problem,
![]()
Conversion of miles to meters
![]()
Frame of Reference
By choosing the origin to be the location of the car when the driver starts to look away from the road we make xo = 0.
This is also the time when we start the clock.
Relevant Physics:
Since the car is moving at a constant speed in a straight line, the one dimensional, kinematic equations for constant velocity apply to this problem.
Placing the origin at the moment the driver "lights up", xo = 0. Expressed in the symbol chosen the position of the car as a function of time relative to the origin chosen,
xc = vc t
A) Find the distance traveled in 3.50 sec.
Because the car is moving at a constant speed the generic equation for the distance the car moves as a function of time is given by
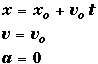
Placing the frame of reference so that the origin is located at position of the car when the driver becomes distracted eliminates xo since it will be zero. Using the personal labels we chose,
![]()
If the car's length is 5 m, then this would mean that the car would travel 117/5 = 23 car lengths in the 3.50 seconds it takes to "light up" or "tune in".
(B) Find the time to travel 1/4 mile.
Solving v = x / t or x = v t for t,
![]()
Physical Variables Used to Measure Motion |
||
Variables |
Meaning |
Symbol(s) |
Time |
The Moment of occurrence of some Event. |
t, T, t |
Location |
Position of the object relative to some origin at time t |
x, y, z, d, s |
Velocity (Speed) |
Rate of Change in an object's Spatial location at time t. |
v, u |
Acceleration |
Rate of Change of an object's Velocity at a time t. |
a, g |
Meaning of Sign of the Variables of Motion for One Dimensional Motion
Frame of Reference:
Before we can talk about the meaning of the sign of a variable we must first specify the frame of reference from which we will view the motion of some object. The following choices are up to you to specify and your choice will determine the outcome of the meaning of the sign of a variable. We will assume the body is moving horizontally.
Spacial Frame:
We also need to stipulate were the origin is located and which direction relative to the origin – to the right or left – will be taken as the positive direction. We will assume the normal convention that the positive direction is to the right of the origin.
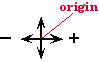
Time Frame:
We also need to specify when we will start the clock – the origin of time.
Time Variable t:
t > 0 – some moment after the instant we start the clock.
t < 0 – some moment before the instant we start the clock.
Position Variable x:
x > 0 – the body is to the right of the chosen origin.
x < 0 – the body is to the left of the chosen origin.
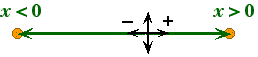
- By shifting the origin one could make the value of the position of a body either positive or negative.
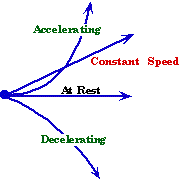
Velocity Variable v:
v > 0 – the body is moving to the right. The body could be either to the right or left of the origin.
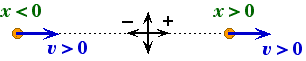
v < 0 – the body is moving to the left. The body could be either to the right or left of the origin.
Acceleration Variable a:
a > 0 – the body is increasing its speed in the positive x-direction. This is not dependent upon whither the body’s velocity vis to the right or left.
a < 0 – the body is increasing its speed in the negative x-direction. This is not dependent upon whither the bodies velocity vis to the right or left.
- Changing the location of the origin will have no effect on the sign or value of the body’s acceleration. What would change the sign of the body’s acceleration is our choice of which direction (to the right or left) is taken to be the positive direction.
- An object is commonly said to be accelerating if both a and v are in the same direction – either ( v > 0 and a > 0 – the body is accelerating in the positively chosen direction) or ( v < 0 and a < 0 - the body is accelerating in the negatively chosen direction). An object could be accelerating even if its value of acceleration is negative provided the object is also moving in the negative direction.
- An object is commonly said to be decelerating if a and v are in opposite directions – either ( v > 0 and a < 0) or ( v < 0 and a > 0) .
VELOCITY (Speed)
- Speed is a measure of how fast an object is moving.
- The technical definition of speed is that it is the rate of change of an object's position with time.
Definition |
Units: |
||||
|
|
- The symbol v, short for v(t), represent an object's speed at a single moment of time.
- The average speed can be thought of as the time average of an object's instantaneous speed in the interval between two different times.
- When an object's speed is constant then the object's instantaneous speed and average speed are identical. Moreover,
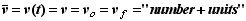
Calculus Relationship
An object's instantaneous velocity function v(t) is the derivative of the object's position function x(t) with respect to time. |
|
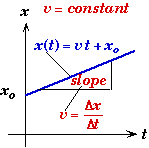
Space -Time Plot
The velocity of an object at some moment of time is the slope the object's position function x(t) at that moment. The tangent of an object's world line -- the space-time curve of the object's location as a function of time -- is equal to the object's velocity at the location of the tangent. |
|
ACCELERATION
- Acceleration measures how fast an object's speed is getting faster (or slower if negative).
- Technically, the acceleration of an object is the rate of change of an object's Speed with time.
Definition: |
Units: |
||||
|
|
The acceleration is Not a measure of the rate of movement of and object in space. It measures how fast an object's speed is getting faster (or slower). In fact it is possible for an object to be at rest at some moment and till have an acceleration even though it has no speed at that moment - see Sign of the Acceleration.
Calculus Relationship
An object's instantaneous acceleration function a(t) is the derivative of the object's velocity function v(t) with respect to time. |
|
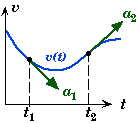
Velocity-Time Plot
The acceleration of an object at some moment "t" is the slope of the object's velocity function v(t) at that moment. This means that a(t) at t is tangent to velocity versus time curve. |
|
One-Dimensional Kinematic Equations for Constant Acceleration
|
Sign of the Acceleration
- The symbol for the acceleration " a " in physics can be positive, negative, or zero.
- In everyday language, we distinguish between a body having a positive acceleration and a negative acceleration by saying that the object is accelerating or decelerating. In physics, we say that a body has an acceleration that could be positive, negative, or even zero.
- It is not always correct to infer that if a body is decelerating that its speed is decreasing, unless you also mean that the positive direction of the frame of reference (which you are subconsciously using to describe the motion) is also in the same direction as the body is moving at that moment.
Free-Fall Example:
When you throw an object vertically upwards, its speed decreases as it goes up and increases as it comes down. Thus one might say that the object is decelerating on the way up and accelerating on the down. From this you might infer that it has no acceleration at all at the top of the motion, but that is not true. The first two statements are correct if you switch the frame of reference on the way down so that the positive direction is now down instead of up.
In physics we can use just one frame of reference to describe both the body's upward and downward motion. Choosing up as positive, we would say the object's acceleration is -9.80 m/s2 both on the way up and the way down, and at the top of its motion.
On its way up its speed is increasing by 9.80 m/s every second in the downward direction. Since it is moving upwards initially, the numerical magnitude of its speed is getting smaller, and it is reasonable to say that the object is decelerating., or accelerating with a negative acceleration.
On the way down, the object's speed is still increasing by 9.80 m/s every second in the downward direction. Since it is moving downwards, the numerical value of its speed is getting bigger, thus leading to the statement that it is accelerating.
At the top of its motion, the object still has an non-zero acceleration. It does not momentarily go to zero. There are two ways that to show that the acceleration is not zero at the top of its motion.
1. At the top of its motion the speed of the object is zero. The acceleration is defined as the instantaneous change in an object's speed with time, a = dv/dt . If it has no speed and no change in speed, then it should just come to a halt and stay there when it reaches the top of its motion. It obviously does not say there, so it must change speed and have an acceleration. This argument is true no matter how small an time interval you pick near the top since the derivative is the limit as the time interval goes to zero.
2. A more physical argument come from the cause of the object's acceleration - the force of gravity. The force of gravity on the objects does not go to zero at the top of an object's motion, or at anywhere else. The force of gravity is always the same and is equal to the object's weight.
Problem-Solving Suggestions for One-Dimensional Constant Acceleration or Velocity Problems
- The following statements/equations are valid when an object is moving at a constant speed provided you set the acceleration a = 0, i.e. constant speed is a special case of constant acceleration when the acceleration is zero.
- The first thing we know is that generic equation for uniform accelerated apply,
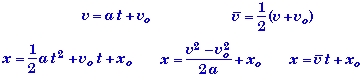
- Identifying the Variables: One essential operation in solving any problem is turning the verbal statement of the problem into a set of mathematical statements by identifying what is given, what is requested, and what is implied.
Verbal meaning of some of the variables used in the generic kinematic equations.
Variable |
Meaning |
|
Initial or staring position of an object. |
|
Final location or position of an object. |
|
The distance an object travels. |
|
Initial or starting velocity of an object. |
|
Final velocity of an object. |
|
The change in object's speed. |
|
The average velocity of the object. |
|
The object's acceleration |
|
The starting time. If the clock is started |
|
The final time. |
- In any (kinematic) problem you will know the value of some of these variables and be requested to find the value of others. The only difference between a given and an unknown is your current state of awareness of its value. What is an unknown in one problem may be a given in another problem. A variable switches from an unknown to a known when you find its value (or its value is explicitly given or implied in the verbal statement of the problem).
- Each of the generic kinematic equations involves a certain subset of variables and constants used to describe motion.
- Note that the different equations in a given set are all identical (provided to= 0). They are just expressed in a different structural forms.
- The decision of which equation to use in any given problem involves looking at what subset of variables you know and what subset you don't know.
- If you know all of the variables but one in some subset, then you can use one of the associated equations in that subset to find the unknown variable.
- Also observe that it is not necessary to always solve a problem directly by finding the one equation that you can plug the knowns into and crank out the unknown - the bottom line equation. It is often useful to use a two-step method where you solve for some intermediate variable that you don't know (and which may not even be requested). Then use this new known variable in yet another equation to find the unknown requested.
Braking Car
A car moving at 85.0 km/hr brakes to a halt in 9.30 seconds. |
|
(A) |
What is the car's average acceleration while it is stopping ? |
(B) |
If the car travels 115 m before it actually comes to a halt, could the car's acceleration be constant ? |
Sketch
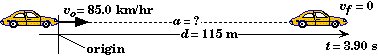
A moving automobile brakes to a stop.
Givens and Labels:
This problem is simple enough that we can use the same labels as those in the generic equations that apply to uniform accelerating motion.
vo |
= 85.0 km/hr |
(Initial speed of the car) |
|
= 23.611 m/s |
(Conversion to SI units) |
vf |
= 0 |
(Final speed of the car) |
ts |
= 9.30 s |
(Time to come to a stop) |
a |
= ? |
(Average Acceleration of the car) |
d |
= 115 m |
(Distance traveled in part B) |
Reference Frame:
Location of the car when the brakes are applied. This implies that xo = 0.
Clocks starts when the brakes are applied. This implies that to = 0.
RELEVANT PHYSICS:
An object's average acceleration is same as the object's acceleration when the object is moving at a constant acceleration. Thus the equations for constant acceleration apply.
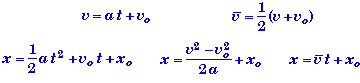
Your main task is identify which variables are known, which variables values are implied by the statement of the problem or your choice of the origin, and which variables are unknown. In this problem we know the initial velocity of the car vo = 85.0 km/s, the time of travel t = 3.90 s, and implicitly the final velocity v = 0. By placing the origin at the location were the car starts to decelerate we know that the car's initial position is zero xo = 0. What we don't know is the distance the car travels x, and the car's acceleration a.
(A) Find the acceleration if a is constant.
The easiest way to determine the acceleration is to use the definition of acceleration, with the realization that when the acceleration is constant then the average acceleration and the instantaneous acceleration are the same.
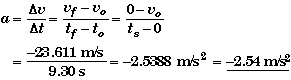
One might also start with the equation of motion of velocity and solve it for a.
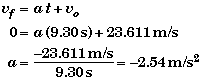
In either case the acceleration turns out to be negative -- indicating that the object is decelerating or slowing down.
(B) Determine if a is constant knowing that the car moves 115 m before it comes to a halt.
If the car's acceleration is constant then we should be able to calculate the distance it would take the car to come to a halt and compare this with the distance of 115 m stated in the problem.
Method I:
We have two choices of how to calculate the distance the car travels:
Since we know a = -2.5388 m/s2 from part A,
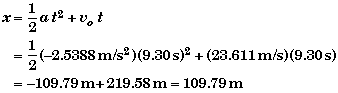
Method II:
We can also find the distance from just a knowledge of information given in the statement of the problem without having to calculate a first.
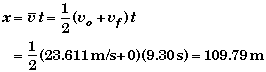
These are not the only two methods that one could use to find the distance. There are many paths to any solution.
In either case the car would have stopped in a shorter distance than 115 m if its acceleration were uniform throughout the car's motion.
Note that if the problem has stated that the car went 110 m before stopping rather than 115 m, then all one could say is that the car's acceleration could have been constant to an accuracy of 3 significant figures. It is quite possible for the car to accelerate and decelerate in such a way that it would only go 110 m before coming to a halt. What would be the same is that the average acceleration would be the same as the value we obtain for a constant acceleration situation.
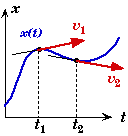
Graphical Interpretation - Space Time Diagrams
- A Space-Time diagram is constructed when one spacial axis is replaced with time and the object's equation of motion x(t) is plotted as a curve on that diagram.
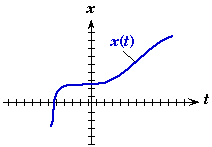
- A Space-Time diagram gives a visual picture of the motion of an object as a function of time. Even when the motion is complex, it is useful to see what is happening to object's location as function of time.
- A Space-Time diagram could be looked at as being constructed from a motion picture of the object's movement over time. By cutting the resulting film strip up into individual frames and then placing them side by side along the t-axis would produce a space-time diagram of the object's motion.
- The curve of an object's equation of motion on a space-time graph is called a worldline. A single point on that curve is called an event; it simultaneously represents both a location and time.
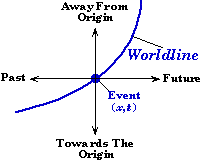
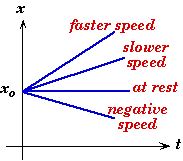
- Straight worldlines on a space-time diagram represent uniform motion, i.e. the object is moving at a constant speed.
|
|
- The slope of the worldline is equal to the velocity of the object at that moment.
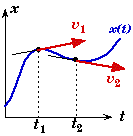
- Curved worldlines on a space-time diagram represent accelerated motion.
- For objects undergoing constant acceleration, their space-time diagrams form a parabola.
- A Space-Time diagram is purely conceptual -- you cannot look out a window and see a car or a rock following a distance versus time curve.
- A horizontal worldline on a space-time diagram represents no motion at all -- the object is at rest.
- It is tempting to talk about an object's motion along its worldline on a space-time diagram. Doing so invokes the idea of some "super-time" which is related to the rate at which an object moves through time -- a meaningless concept unless you assert that it is always uniform, i.e. that mother nature does not speed up or slow down the rate at which nature's camera is running. A worldline represents a "frozen space-time" picture in that it simultaneously contains the total history of the object motion through space as a function of time.
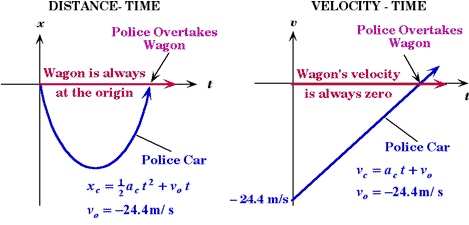
Police Car Chases a Station Wagon
A station wagon moving at a constant speed of 88.0 km/hr passes a parked police car. At the moment the station wagon passes the police car, the police car starts accelerating uniformly at a rate of 10.8 km/hr each second.
(A) |
How long will it take the police car to overtake the station wagon ? |
(B) |
How far will the police car travel before it overtakes the station wagon ? |
How fast will the police car be moving when it overtakes the station wagon ? |
|
Make a graph of both the distance versus time and the speed versus time for both vehicles. |
|
(E) |
What excuse did the driver offer to the policeman ? |
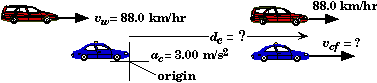
A police car accelerates to catch a station wagon moving at a constant speed. The police car starts from rest the moment the station wagon passes.
The Frame of Reference
Reflective Mental Overseer Questions:
- From what point of view will I choose to observe the action described in this problem ?
- Where will I place the origin and when will I start the clock running ?
Actions:
- Designate the location of the frame of reference in some manner like placing a "+" at the origin of the coordinate system on your sketch. This determines the value of xo. Normally xo = 0 if you place the origin at the initial location of an object. When two or more objects are present, the initial position of all the objects cannot be zero unless they are at the same point initially.
- Choose when you will start the clock. This determines the value of to. Normally to= 0 if you start the clock at the start of some action.
- Choose which direction will be positive and which direction will be negative. Normally, directions to the right are taken to be positive as are directions upwards.
- For rotational problems choose either clockwise or counterclockwise as the positive rotational direction.
Comment:
- The structural form of the equations that you generate to solve a problem will be different for different locations of the origin.
- Some frames of reference produce easier equations to solve.
- Switching your frame of reference in the middle of a solution will almost always lead to disaster unless you are consciously aware that you are doing so.
- The generic equations in the book generally apply to a particular frame of reference which you will need to modify to fit your selected point of reference.
- A frame of reference could also be moving.
Givens and Labels:
In this problem we will need to generate our own personal labels for the variable since there are two objects. Otherwise how will we keep track of wither v stands for the velocity of the car or the velocity of the wagon. One way is just attach subscripts the variables of motion x, v, and a. Note that we only need one symbol for time since there is not a separate time associated with the two automobiles.
Station Wagon
aw |
= 0 |
(No acceleration) |
vw |
= 88.0 km/hr |
(Constant speed) |
|
= 24.444 m/s |
(Conversion to SI units) |
dw |
= ? |
(Distance traveled by wagon after it passes the police car) |
Police Car
ac |
= 10.8 km/hr/s |
(Constant acceleration) |
|
= 3.0000 m/s2 |
(Conversion to SI units) |
vco |
= 0 |
(Initial velocity of police car) |
vcf |
= ? |
(Final velocity of police car when it catches the wagon) |
dc |
= ? |
(Distance travel by police car) |
t |
= ? |
(Time to over take the wagon) |
We could have eliminated the subscript for the acceleration of the police car since the wagon's acceleration is zero and no confusion would arise.
Note that we could ignore the length of the two autos since the distance they travel is large compared their size. However, by skillfully placing of the origin and starting time the lengths do not come into play (see Frame of Reference).
Frame of Reference
Unless we ignore the length of the two vehicles, the statement of the problem is ambiguous about what is meant by "moment the station wagon passes the police car". By interpreting this to mean the moment the rear end of the station wagon passes the front of the police car we can choose this moment to start the clock for either frame.
Stationary Frame:
The most natural place to locate the origin is at the location of the police car before it starts to accelerate. To be more precise, place the origin at the front of the police car.
Relevant Physics:
The kinematic equations for constant acceleration apply to both the police car and the station wagon. The station wagon has a constant speed so its acceleration is equal to zero.
Since there is two automobiles involved that kinematic equations apply we will have to use personal labels to distinguish say the velocity of the cop car from the station wagon. Using the labels chosen in the information given, the generic kinematic equations of motion of the police car and wagon becomes:
Stationary Frame:
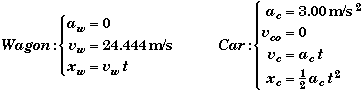
Moving Fame:
In this frame the station wagon's speed is zero and is located at the origin.
As view from inside the station wagon, the police car is moving "backwards" initially at a constant speed of 88.0 km/hr towards the wagon. At the moment it passes the wagon the police car begins to accelerate in the forward direction at a rate of 3.00 m/s2. After the clock starts the police car moves back away from the wagon, slows down, comes to a stop, and then moves forward towards the wagon.

(A) Find the time t when the police car overtakes the station wagon.
The trick to solving this problem is recognizing that both automobiles have traveled the same distance when the police car catches up to the station wagon. Setting xw equal to xc we have an equation that only involves time and the two givens that are known - namely the velocity of the wagon vw and the acceleration of the car ac. See Relevant Physics for the origin of the variables used below.
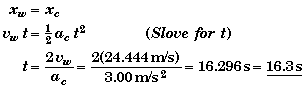
Moving Frame Solution:
From the point of view of the station wagon, the final location of the police car when it catches up is zero - it is back at the origin attached to the station wagon. Thus the problem is that of finding the times when the police car is at the origin.
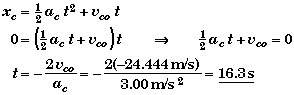
Note that the other solution, t = 0, represents the time when the station wagon passed the police car and we started the clock. Also note that the initial velocity of the police car vco is no longer zero in the moving frame but is equal to the velocity of the moving frame - namely the negative the velocity of the wagon in rest frame, -24.444 m/s.
(B) Find the distance xc when the police car catches up to the station wagon.
Since we know the time when the car catches up from part (A) to be 16.286 s,
![]()
Symbolic Solution:
Again using the results of part A, we know that t = [2 vw /ac]2.
![]()
Alternate Solution:
Since the station wagon travels the same distance as the police car, we could have just looked for the distance the wagon travels,
![]()
Alternate Solution not using the time:
Assuming we do not know the time from part A, how would we find the distance? An approach one might employ is to use the generic kinematics equation for the police car that does not involve time,
![]()
Using the symbols chosen, this equation becomes
![]()
To use this solution we would need to know the final velocity of the police car which we have not determined yet. However, we know that both automobiles travel the same distance in same time. Thus they must have the same average velocity.
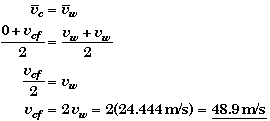
This means that the police car's final velocity will always be equal to twice the wagon's velocity regardless of the initial speed of the station wagon or the acceleration of the police car.
Symbolically this gives
![]()
which is identical to the solution we found previously.
Moving Frame Solution:
The distance traveled by the police car in the statement of the problem refers to a distance measured in the stationary frame. In the moving frame there is no object stated which can be associated with the stationary frame. We could imagine that the police car was parked by (or behind) a billboard. Such a billboard would be observed to move at a constant speed of 88.0 km/hr to the left in the wagon's frame. Translated into the moving frame, the question becomes how far is the police car from the billboard when the police car returns to the origin of the moving frame ,i.e. catches up with the station wagon? This is just the distance of the billboard from the wagon at t = 16.296 s. This distance is given by,
![]()
which is also identical to the value we found earlier.
(C) Find the police car's speed, vcf, when it catches the station wagon.
Numerical Solution::
See part A for the derivation of the time.
![]()
This answer shows that the problem is not very realistic because the police car would then be traveling at 176 km/hr which is twice the speed of the station wagon.
Symbolic Solution::
![]()
Again this shows that the police car will be traveling twice as fast as the station wagon when it catches up no matter what the initial velocity of the wagon or the acceleration of the police car. This show one of the advantages of a symbolic solution over a purely numerical solution.
Alternate Solution::
Since the police car and the station wagon travel the same distance in the same amount of time, they must have the same average velocity,
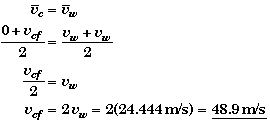
Moving Frame Solution:
The velocity of the police car when it returns to the origin in the moving frame is given by
![]()
If we jump back into the stationary frame we will have to add the velocity of the moving frame, 24.444 m/s, to this value in order to determine the car's speed as seen by a stationary observer.
![]()
This is identical to what we found previously.
(D) Sketch the space-time motion.
Stationary Frame:
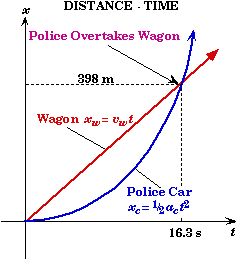
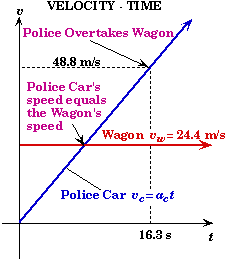
Moving Frame:
Gravitational Free Fall
Generic Equations of Motion 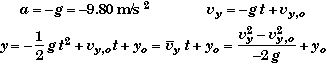 |
Information Implied |
Frame of Reference |
|
Law of Fall Bodies |
|
Derivation |
The upward direction is taken as the positive direction. If the origin is taken at ground level, then:
yo |
is the initial height of the object at time zero. |
vy,o |
is the initial velocity of the object in the y-direction. |
Information Implied:
When an object is propelled into the air, it is assumed that all other forces acting on the object except gravity are negligible. This means that:
- We neglect any effects due to air resistance on the object.
- We neglect any effects due to the Earth's rotation.
- We assume that the object does not rise high enough for the acceleration of gravity to change .
With these assumptions the body's acceleration is both constant and downward regardless of its direction of motion or its height above the ground. This means that object's acceleration is downwards regardless of weather the object is moving upwards or downwards, a = -g = -9.80 m/s2 .
Frame of Reference:
The freefall equations above were derived by assuming the upward y-direction is the positive direction and the clock starts at time t = 0. The sign of the acceleration is negative and it equal to a = -g . (When an object is moving downwards, its velocity will be a negative number using this frame of reference.)
It is possible and sometimes useful to take the downward direction as positive. In this case the equations of motion will not be identical to those above. Typically one would use this frame if the object's motion was all downwards like a ball thrown downwards from the top of a building. The main difference between these two frames is the sign of the velocity and acceleration.
The Law of Falling Bodies:
In the absence of air resistance, any two bodies that are dropped from rest at the same moment will reach the ground at the same time regardless of their mass.
A stronger statement is: The acceleration of all objects is the same in the absence of air resistance. As long as an object is in freefall - regardless if it is going up, down or sideways - its acceleration is equal to 9.80 m/s2downwards.
Law of Falling Bodies:
Two identical objects except with different masses are dropped from the same height at the same time. With air resistance set to zero, both balls strike the ground at the same time. As the air resistance is increased, the more massive object will strike the ground first. With enough air resistance the lighter ball is seen to reach a terminal velocity. Displayed is the distance vs. time, velocity vs. time, and the acceleration vs. time diagrams.
Derivation of the Free-Fall Equations:
Since we usually associate the vertical direction with the y-axis, we will transform the generic equations for constant acceleration by first replacing " x " with " y ", " a " with "-g ", and " v " with " vy ".
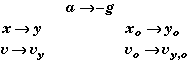
Then,
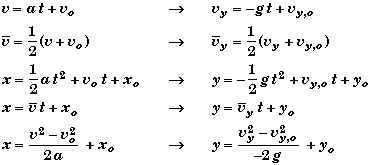
Normally one might omit the subscript y on the velocity v , if the motions is only in the vertical direction. If you do omit the subscript be aware that your are doing so because there can be no notional confusion when the motion is only vertical. This is not the case for projectile motion problems where an object can have both horizontal and vertical motion in the x and y directions at the same time. In such problems is important to keep in mind that it is only the vertical component of an object's velocity that is affected by gravity and that the vertical component vy and horizontal component vx of an object's velocity are different variables.
Vertical Ball Toss
One student stands on the top a 45.0 m building. Another student stands on the ground and throws a ball vertically to the student on the top of the building who reaches out to catch the ball. Neglecting the height of the students:
(A) |
What is the minimum vertical speed at which the ball must be launched so that it just reaches the student on the top of the building ? |
(B) |
How long will it take the ball to rise to its highest point (the top of the building) after it is launched ? |
(C) |
What is the speed of the ball when it has risen to half its maximum height ? |
(D) |
If the ball is not caught, what is the speed and direction of the ball 4.40 seconds after it was launched ? |
Sketch:
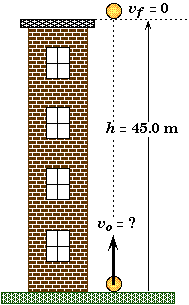 |
A vertically launched ball rises |
Givens and Labels:
h |
= 45.0 m |
(Maximum height the ball attains.) |
yo |
= 0 |
(Initial location of the ball. ) |
vf |
= 0 |
(Final velocity of the ball at the top.) |
vo |
= ? |
(Initial velocity of the ball.) |
tr |
= ? |
(Time of rise.) |
We assume that distance the ball is above the ground when it is launched is the same as the distance it is above the top of the building when it is caught, so that total distance traveled by the ball is the same as the height of the building, 45.0 m. This is the same as neglecting the height of the students compared to the height of the building.
Reference Frame:
The most convenient place to locate the origin is at the launch point when the ball leaves the student's hand.
We take up as the positive direction.
We start the clock when the ball is launched.
These last two choices allow us to use the generic freefall equations of motion to solve the problem.
RELEVANT PHYSICS:
Once the ball leaves the student's hand it is in free-fall. Neglecting air resistance the ball's acceleration is 9.80 m/s2 in the downward direction both on its way up and its way down. This means that we do not have a different set of equations for the ball's upward motion and its downward motion.
In this problem we can use the generics equation for freefall since there is only one object involve (the ball) provided we use the same frame of reference as the generic freefall equations.
The relevant freefall equations for the ball height and velocity of the ball are:
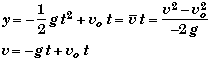
(A) Find launching speed vo.
Since we do not know the time it takes the ball to rise to its maximum height, the only freefall equation that does not involve time directly is
![]()
When the ball reaches the top of its trajectory, then y = h and v = vf = 0. Placing these into the above equation we can solve for the initial velocity.
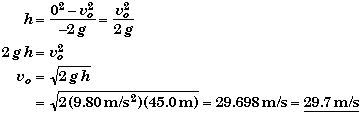
An alternate solution would be to solve for the time first and then use it to find the initial velocity. In part B we will show that the time of rise is given by
![]()
Plugging this into the velocity equation and solving for the initial velocity,
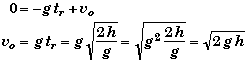
which is the same equation as before.
Knowing the time, we could have also found vo using the distance equation, but it requires more algebra to reduce it to the same form as before.
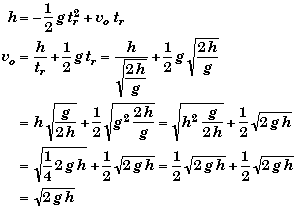
All these alternate derivations shows that we most likely solving the problem correctly since these different methods give the same results.
(B) Find the time of rise tr.
There are two different ways to find the time of rise tr. The easiest way uses the value found in A for the initial velocity vo. A second way - a trickier one - involves changing your frame of reference.
Solution using vo.
When the ball reaches the top of it trajectory, its velocity is zero. Applying the velocity equation at this moment and solving for the time of rise,
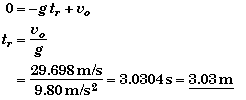
Symbolically in term of the values stated in the problem,
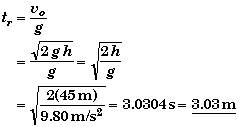
Direct solution:
If you examine the generic equations of motion you can see that all the equations involve vo as an unknown. Therefore it is not possible to find the time of rise directly without first finding the initial velocity. However, it is possible to look at the problem from a different point of view and find tr directly. If you drop a ball from the top of the building it will take the same amount of time to reach the ground as it takes to rise to the top - the time of rise is equal to the time of fall since the acceleration in both cases is the same.
If we move our origin to the top of the building, then the ball's initial velocity will be zero. Choosing up as positive, the distance fallen in a time tr is -h. The freefall equation evaluated at tr becomes,
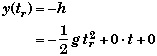
Solving for the time, we get same symbolic relations as above.
![]()
(C) Find the speed of the ball half way up, when y= h/2.
The quickest way to find the velocity half way up is to use the freefall equation that does not involve the time
![]()
Evaluating this equation at y = h/2 and solving for v we get,
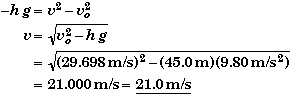
Note that the velocity half way up is greater than half the initial velocity of 29.7 m/s because the ball spends a lot more time during the last half of its vertical rise than it does the first half -- the ball is moving slower the higher it rises. Why is the answer not equal to half the initial speed?
General Symbolic Solution:
It is possible to determine a single equation that would give the velocity at any height directly, knowing the ball's maximum height h. From part A we know that
![]()
Place this into
![]()
and solve for the velocity v
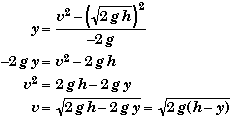
With hindsight we understand how this equation works. When we started from the ground the initial velocity needed to reach a height h was ![]() . Thus if we move up a distance y, then the maximum height above this point is (h - y) so that the speed needed to go (h - y) will be
. Thus if we move up a distance y, then the maximum height above this point is (h - y) so that the speed needed to go (h - y) will be ![]() .
.
When y= h/2 we get
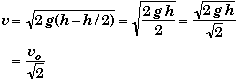
Thus we see that the velocity half way up is not one half the initial velocity but 1 over square root of 2 smaller, because the distance is related to the velocity squared.
![]()
(D) Find speed of the ball when t = 4.40 s if it is not caught.
There is no one generic free-fall equation that will allow you find the speed directly knowing only the time and the height. You would need to find the initial velocity or the time of rise first and then use it to find the speed at 4.40 s.
Solution using the initial velocity:
The freefall equations of motion apply to the motion of the ball all the way up and all the way down. Thus we could use velocity equaton to find the velocity at any time, provided we know the initial velocity which we found in part A.
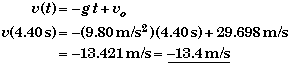
The negative sign means that the ball is moving downwards.
Solution using the time of rise:
Since 4.40 s is longer than the time of rise tr = 3.0304 s ( found in part B) the ball must be on its way down. The time it takes the ball to fall from it highest position to it location at 4.40 s is 4.40 s - 3.0304 s = 1.3695 s. Moving to a frame of reference located at top of the ball's motion and starting the clock at this moment, the equation for the velocity is then
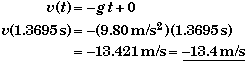
Summary Problem:
Rising Rocket
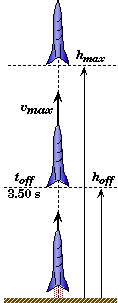
A toy rocket is observed to accelerate upwards at a uniform acceleration of 12.5 m/s2for 3.50 s before its engine shuts off. If air resistance is negligible: |
|
(A) |
What is the maximum upward speed the rocket will be moving when its engine shuts down ? |
(B) |
What is the maximum height that the rocket will reach above the ground ? |
(C) |
How long will the rocket be in flight ? |
(D) |
How fast will the rocket be moving when it returns to the ground ? |
Sketch:
 |
|
|
|
||
The rocket continues upwards after its engine shuts off until it reaches its maximum height. The rocket then falls back to the ground. |
|
||||
After the engine shuts down, the upward moving rocket is then accelerated downwards by gravity. The rocket is in free-fall. |
|
||||
Engine shuts off at 3.50 s. |
|
|
|
||
A rocket accelerates upwards at 12.5 m/s2 while its engine is running. |
|
||||
Personal Labels and Information Implied or Requested
aR |
= 12.5 m/s2 |
(Acceleration of the rocket for the first 3.50 s) |
aR |
= -9.80 m/s2 |
(Acceleration of the rocket after 3.50 s) |
t |
= ? |
(Time measured from the moment of launch) |
t' |
= t - 3.50 s = ? |
(Time measured after the engine shuts off) |
toff |
= 3.50 s |
(Time until the engine shuts off) |
tf |
= ? |
(Total time of flight) |
t'f |
= ? |
(Time of flight after the engine shuts off) |
t'top |
= ? |
(Time to reach maximum height after the engine shuts off) |
t'' |
= ? |
(Time measure after the rocket reaches its maximum height) |
t''fall |
= ? |
(Time of fall from the rocket's maximum height to the ground) |
vmax |
= ? |
(Maximum upward speed of the rocket) |
vg |
= ? |
(Rocket's speed when it first strikes the ground) |
hmax |
= ? |
(Maximum height of the rocket will reach above the ground) |
hoff |
= ? |
(Height of the rocket when the engine shuts off) |
Why is the rocket's upward acceleration not equal to: 12.5 m/s2 - 9.80 m/s2 = 2.70 m/s2 ?
Frame of Reference
Location of the rocket at take off with up as the positive direction.
The clock starts when the rocket is launched.
In this problem we will show how to solve the second half of the problem - after the engine shuts off - as a separate problem by starting off the clock when the engine shuts off.
It is also useful to consider yet another clock start when the rocket reaches it maximum altitude.
Relevant Physics
The trick to solving this problem is realizing that the problem can be separated into two constant acceleration problems. Both before and after the rocket's engine shuts off, the rocket is accelerating uniformly but by different amounts. Because there will be two different (but related) parts to this problem that use the same generic equations it is beneficial to generate personal labels in this problem ( see Givens).
Before the engine shuts off, the rocket's equations of motion will be
![]()
After the rocket engine shuts off, the rocket is in free-fall.
The easiest way to use the free-fall equations is to look at this part of the problem as a separate problem in which we re-start the clock at the instant the engine shuts off.
It is tempting to jump to the conclusion that the answer should be just half the initial velocity since the ball is half way up to its maximum height. For this to be true would mean that the velocity and the distance would have to be directly proportional to each other. However,
This is considerably more complex than a simple linear relationship between v and y.
Note that the velocity is equal to half the initial velocity when t = tr/2 because v and t are linearly related by y = -g t + vo.
Another way to see that this could not be true is to ask what would happen if the initial velocity were doubled - would the ball rise twice as high? No, it would rise more than twice as high. Why? From part A we know that
Doubling the initial velocity to 2vo gives,
Thus the ball will go four times higher!
It is tempting to say that the rocket's upward acceleration must be 12.5 m/s2 - 9.80 m/s2 = 2.70 m/s2 since gravity is trying to accelerate the rocket downwards at 9.80 m/s2. If this was the case then what would we say the rocket's upward acceleration is, 2.70 m/s2 or 12.5 m/s2 ? It cannot be both.
Gravity is surely acting on the rocket as it goes up, but if the rocket is observed to accelerate upwards at 12.5 m/s2 then the effect of gravity must already be accounted for in the observation. If the problem had stated that the rocket could accelerate at 12.5 m/s2 in the absence of gravity, then its upward acceleration would be 2.70 m/s2.
Let us represent this new time by t' so that we do not confuse it with the time from launch, t. Note that most students would not use a different symbol because they could keep track of the meaning of the symbol t by the context in which they are using the symbol. We use a different symbol so that it will be clear which time we mean.
The initial position and velocity of the rocket at new t' = 0 are hoff and vmax. The second part of this problem is equivalent to the problem of a rock being launched vertically from the top of a building that is hoff meters high, with an initial upwards velocity of vmax meters per second.
After 3.50 seconds the equations of motion of the rocket become:
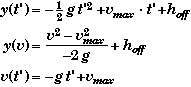
We do not know hoff or vmax yet, but we can find them since they are the height and velocity of the rocket when t = 3.50 s.
Observe that it is possible to express the equations of motion of the rocket when the time is greater than 3.50 s without re-starting the clock. The equations would look like,
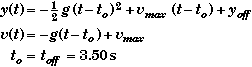
Here t represents the time measured from launch time throughout the problem. The time to is the time after launch when the rocket goes into freefall motion, which is the same as toff. We choose not to use these equations because they would be harder to manipulate when trying to solve for the time. Moreover, These equations are not valid before 3.50 s. When the time is less than 3.50 s the equations of motion are still
![]()
(A) Find the rocket's maximum velocity, vmax.
The rocket starts off with no velocity and reaches its maximum speed at the moment the engine shuts off - it begins to decelerate after that moment. This is when t = toff = 3.50 s. Since the rocket is accelerating upward at a constant acceleration we can find the velocity at toff using the velocity equation that apply to objects undergoing constant acceleration.
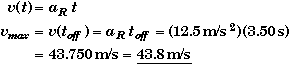
(B) Find the rocket's maximum height, hmax.
We could find the maximum height if we first found the height of the rocket at shut off, hoff, and then added to this the distance the rocket will rise from hoff to its maximum height when it is in free fall.
The relevant physics equations that apply to this problem are different before and after the engine shuts off.
After the engine shuts off the relevant equations that apply are:
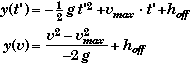
We could use either of these two equations to find hmax. Examining the first equation we see that it uses time, while the second equation uses only velocities. If we knew the time that it took the rocket to rise to its maximum height then we could use this information in the first equation to find hmax. (Note that t' is the time after 3.50 seconds, t' = t- 3.50 s.) Since part (C) asks for basically twice that time, we will explore this approach in (C). However, the second equation can be used more directly since it involves knowing what the velocity of the rocket is at the top of its flight, which we know must be zero.
Doing the problem both ways is good practice when you are learning a new concept. It also provides a nice way to check your answer.
For either method we will need to know the height of the rocket when the engine shuts off, hoff., and the speed of the rocket at that moment, vmax, which we found in part A. The unknown, hoff, is not requested by the problem but it can easily be found since t = toff = 3.50 s when y = hoff.
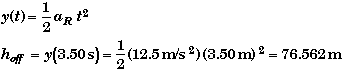
Finding hmax using the time of rise:
In part C we will show that the time it takes the rocket to reach the top of its flight after the engine shuts off will be t'top = 4.4643 sec. Thus
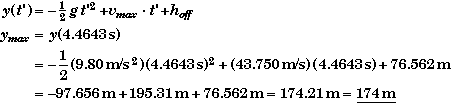
Finding hmax using the velocity at top:
Here we use the equation of motion for the height of the rocket that does not involve time. At the top, the rocket's velocity is zero.
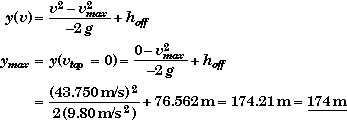
These numbers seem to be in the right ballpark. Answers that were either cm or km high answers should cause your reflective mental overseer to scrutinize your results.
(C) Find tf, the total time the rocket is in flight.
Direct method of finding the time of flight:
When the rocket returns to the ground we know that its height is zero. We can use this fact to solve for the time of flight t'f after 3.50 s. The relevant physics equation that applies after 3.50 s is:
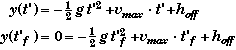
This quadratic equation will have two solutions, one positive and one negative. The positive solution will be the time of fall. Using the general solution of a quadratic equation we find,
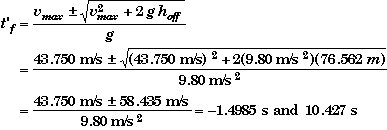
(Another method would be to use the solve mode on your calculator to find the solution of the quadratic t'f.)
The total time of flight is
![]()
Alternate Solution:
When the rocket reaches the top of its flight we know that its velocity will be zero. Using this and the equation of motion for velocity when time is greater than 3.50 s we get,
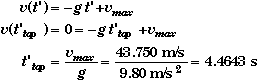
Thus the time it take the rocket to reach the top of its flight is 4.4643 s + 3.50 s = 7.9643 s.
To this we must add the time it takes to fall back to the ground.
We could find this time in two ways.
1. We could find the time of fall using the fact that we know the rocket's maximum height hmax from part (B). The time of fall is also the time it takes an object to fall from rest from a height hmax to the ground. What we are doing is restarting the clock again when the rocket is at the top. For this frame the equations of motion of the rocket then become (since its initial velocity is vtop = 0)
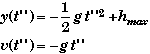
When the rocket reaches the ground we can find the time of fall tfall from
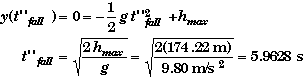
The total time of flight is
![]()
2. A more clever method involves the meaning of the negative solution of the quadratic equations for the time when the rocket would be at y = 0. The negative solution, 1.4985 s, represents the time the rocket would have taken to reach hoff if the rocket were in free-fall from launch. Thus 4.4643 s + 1.4985 s = 5.9628 s represents the time of free-fall rise or fall. The total time of flight would be 7.9643 s + 5.9628 s = 13.927 s, the same value as before.
(D) Find the speed of the rocket when it hits the ground, vg.
After 3.50 s the rocket's velocity is given by
![]()
From part (C) we found that the time the rocket is in the air after 3.50 s to be t'f = 10.427 s. Thus
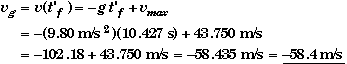
The minus sign means the object is moving downwards.
Alternate Method
We also found in part (C) that the time it takes the rocket to fall from the top of its flight path to the ground to be tfall = 5.9628 s. Starting the clock at the top, the velocity equation will be even simpler (since the initial velocity = vtop = 0 in this frame)
![]()
These are only two of the many paths we could have taken to solve this problem.
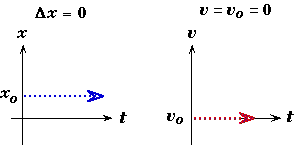
Summary Types of Uniform Motion
UNIFORM POSITION: (Constant x)
Equations of Motion 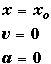 |
|
UNIFORM VELOCITY: (Constant v)
Equations of Motion 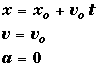 |
|
UNIFORM ACCELERATION: (Constant a)
Equations of Motion 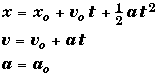 |
|
The Equation of Motion x(t)
The notation x(t) is a shorthand way of symbolizing the fact that an object's location "x" can be expressed as a explicit function of time, x = f(t).
Examples:
For an object undergoing constant acceleration, f(t) = 1/2 a t2 + vo t + xo
For an object executing simple harmonic motion, f(t) = A sin(w t + f)
Note that in addition to being a function of time, x(t) is also a function of other variables. We do not usually express x's explicit dependence upon these other variables, but it is implied.
- Once x(t) is explicitly known, then the history of the motion of the object can be determined.
Location: xA= x(tA)
You know where the object is located at any moment tA by evaluating x(t) at t = tA.
Velocity: vA= v(tA) where v(t) = dx/dt
You know how fast the object is moving at any moment tA by taking the derivative of x(t) with respect to time to find v(t) and then evaluating v(t) at t = tA.
Acceleration: aA = a(tA) where a(t) = dv/dt
You know the acceleration of the object at any moment tA by taking the derivative of v(t) with respect to time to find a(t) and then evaluating a(t) at t = tA
Calculus Relationships between the variables of motion
for one Dimensional Motion
Variable |
Derivative Relations |
Integral Relations |
Position |
|
|
Velocity |
|
|
Acceleration |
|
|
Calculus of Motion Problem
The equation of motion for the velocity of a ladybug on a jet-powered skateboard in a driving wind, moving along a horizontal straight line is given by
![]()
where a = 0.430 m/s3, b = 8.50 m/s, t = 7.40 s.
(A) |
Determine the ladybug's initial speed, and plot the ladybug's velocity versus time diagram between 0 and 18 seconds. |
(B) |
Determine the equation for the ladybug's acceleration as a function of time and calculate the ladybug's initial acceleration. |
(C) |
Plot the ladybug's acceleration versus time diagram between 0 and 18 seconds. Is this ladybug's acceleration constant ? |
(D) |
At what moment will the ladybug's velocity be a minimum, and what will that velocity be ? |
If the ladybug's initial position is at +15.0 m, determine the equation of motion for the ladybug's position as a function of time. Plot the ladybug's distance versus time between 0 and 18 seconds. |
|
At what moment and at what distance from the origin does the ladybug reverse its motion ? |
Sketch and Process:

A ladybug undergoes One-Dimensional motion with a known velocity function.
Givens and Labels:
We can use the generic labels to describe the ladybug's motion:
v(t) |
= a (t - t)2- b |
(Equation of Motion for the Velocity of the ladybug) |
a |
= .430 m/s3 |
(Numerical value of the parameter a) |
b |
= 8.50 m/s |
(Numerical value of the parameter b) |
t |
= 4.70 s |
(Numerical value of the parameter t) |
xo |
= 15.0 m |
(Initial position of the ladybug) |
a(t) |
= ? |
(Equation of Motion for Acceleration) |
x(t) |
= ? |
(Equation of Motion for Position) |
Reference Frame:
It is implied that the ladybug's motion is measured relative to the origin of the x-axis.
It is also implied that clock starts when time is equal to zero.
Relevant Physics:
This problem is mostly a kinematics calculus problem. The relevant physics is that a ladybug's motion can be described using three mathematical functions - one for the ladybug's location, one for the ladybug's velocity, and one for the ladybug's acceleration. Each of these functions is primarily a function of time t -- the parameters a, b, and t being constants. Moreover, the ladybug's location, velocity, and acceleration functions are connected to each other by either a derivative or integral.
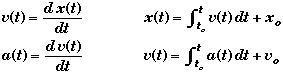
In this problem we are given the ladybug's velocity v(t) so we can find the ladybug's acceleration by taking the derivative of the velocity with respect to time.
To find the ladybug's position as a function of time x(t) we will need to integrate the velocity function over time.
The maximum or minimum of a function can be found by taking the derivative of the function with respect to time, setting the result equal to zero, and solving this expression for the time.
Since the acceleration is the derivative of the velocity, the velocity will have a local maximum or minimum when the acceleration is zero.
The location where the ladybug reverses its direction is also the location where the ladybug's distance from the origin is at a local maximum or minimum. A turn-around point thus occurs when the ladybug's velocity is zero since the velocity is the derivative of ladybug's position.
(A) Find vo and plot v vs. t between 0 and 18 s.
To find the ladybug's initial velocity we only need to evaluate the ladybug's velocity equation at t = 0.
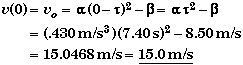
An old and laborious way of plotting v(t) on graph paper would be to calculate the value of v(t) at as many times needed to produce a smooth curve. An easier method would be to use a graphing calculator or a program like Mathcad to plot the velocity function. I use Mathcad since it's easy to cut and paste the resulting graphs into this document.
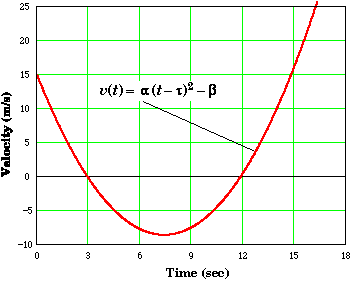
Expanding v(t) in powers of t we can see that the highest power of t is two. This means that the curve should be and is a parabola.
![]()
(B) Find a(t) and determine ao.
To find the function for acceleration we take the derivative of the velocity with respect to time. Expanding the term (t - t)2 in powers of t before taking the derivative we find
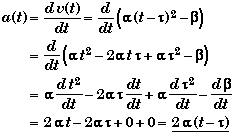
We have used the observation that the derivative of a constant is zero, and
![]()
Alternate Method:
Note that if F(x) is a function of x, then
![]()
Associating F with t - t, then
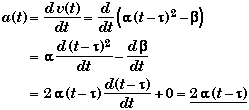
This method is slightly faster since one does not have to carry out the algebraic expansion first.
At t = 0 seconds,
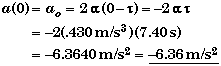
Checking for Consistency:
Since the slope of the velocity curve is equal to the acceleration, then the slope of the velocity curve at t = 0 seconds should be negative. Examining the v vs. t in part A shows that this is the case.
(C) Plot a vs. t and determine if a is constant.
In part B we found that the acceleration is equal to a(t) = 2a(t - t). Plotting this expression we get
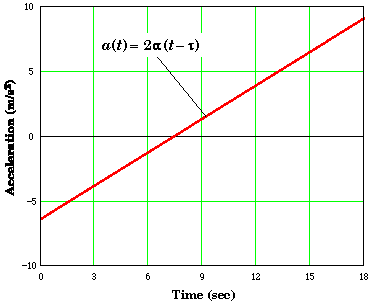
If the acceleration were constant then the plot would be a horizontal straight line. The acceleration is a straight line but it is increasing linearly with time. This could happen if there was a force (say a blowing wind) that was over the period of the problem increasing uniformly with time.
(D) Find the minimum value of v(t).
Mathematically, if a function has a minimum (or maximum) then the derivative of the function at that point will be equal to zero. Since the derivative of the velocity is the acceleration, then we could look for the time tm when the acceleration is equal to zero. Using the equation for the acceleration found in part B,
![]()
We could also deduce this by looking at the plot of v vs. t in part C.
The minimum velocity can then be calculated by plugging this value of time into the velocity equation.
![]()
What is the physical reason why the velocity is maximum or minimum when the acceleration is zero ?
When a is zero the ladybug is no longer speeding up or slowing down at that moment. If the acceleration also changes direction -- changes sign at that moment -- then the ladybug will begin to increase its speed in the opposite direction that it was moving. If the ladybug has a positive velocity that is increasing just before a = 0, then the magnitude of the ladybug's velocity will decrease from that time on, making its velocity at a = 0 into a maximum. In this problem the ladybug has a negative velocity that is decreasing just before a = 0. Thus the ladybug will increase its velocity after a = 0, making its velocity a minimum value at a = 0.
(E) Find x(t) knowing that xo = 15.0 m and plot x vs. t.
From the calculus of motion we know that the position is the integral of the velocity.
![]()
We can easily derive this relation from the definition of instantaneous velocity without having to memorize it as separate rule.
Start with the definition of velocity, multiply both sides by dt, and integrate between the starting conditions (xo, vo, to)and ending conditions (x, v, t).
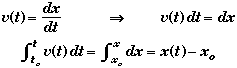
In this problem to= 0.
The most direct way to integrate the velocity function is to expand the velocity function as a power of t before integrating.
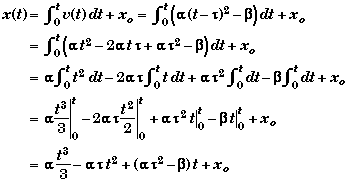
We have used the relations
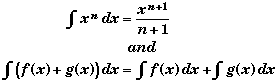
Alternate Method of Integration:
Instead of expanding the velocity function before integrating we could also use a substitution method to integrate the velocity function. Let z = t - t, then dz = dt and

This answer is the same as before but expressed in a different form. If you expand the term (t- t)3in powers of t you will get the identical expression.
Checking The Solution:
One way to check our solution is to differentiate it and see if it gives us the correct velocity function.
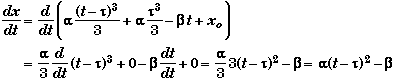
Note that if our solution was wrong because we had the wrong constant of integration, then this method of checking would not work since the derivative of a constant is always zero.
Plotting x(t),
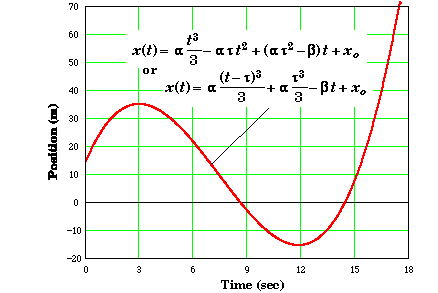
If you were asked to find the time when the ladybug was at some location like the origin, then the position function x(t) is complex enough that the fastest way to solve for the time would be to use the solve mode of a calculator to find the roots of x(t) = 0. You will need to be careful since x is to the third power in t, x will have three zeros. The first time (after t = 0) that the ladybug will be at the origin is at t= 8.63 s. The other two solutions are at -.841 s and 14.4 s.
(F) Find values of x when x(t) is maximum or minimum.
Finding the Time:
Since the velocity is the derivative of the position, then the ladybug will reverse direction when its velocity goes to zero. Thus we need to solve v(t) = a(t - t)2 - b = 0 for its roots. This is simple enough to solve symbolically,
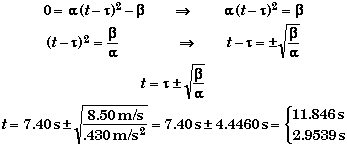
We can verify these values by looking at the plot of v vs. t in part A to see when v(t) = 0.
Finding the Distance:
Using these values for the time in x(t) we found in part E, we can find the location of the ladybug when it reverses direction.
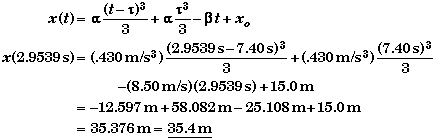
and
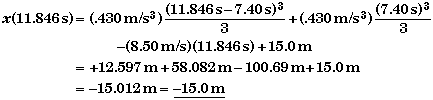
Inspection of x vs. t plot shows that these values are reasonable.
Summary of the Ladybug's Motion:
The ladybug starts off with a positive velocity of 15.0 m/s, 15.0 m to the right of the origin with an initial negative acceleration of -6.36 m/s2. The ladybug's forward motion slows down to a halt at t = 2.95 s when it is 35.4 m from the origin. Its acceleration is still negative and the ladybug begins to move back towards the origin.
At t = 7.40 s the ladybug's velocity reaches a maximum negative value when its acceleration is equal to zero. The acceleration changes from being negative to being positive and the ladybug begins to increase its speed in the positive x-direction. The ladybug is still moving backwards at this moment.
The ladybug crosses the origin at t = 8.63 s with a negative velocity that is getting smaller. At t = 11.8 s the ladybug reverses its direction as it comes to a halt. The ladybug then begins to move in the positive x-direction. It once again crosses the origin at 14.4 seconds with a positive velocity and a positive acceleration.
Derivation of Kinematic Equations for Constant Acceleration
1. Derivation of
![]()
Algebraic Derivation:
Since the acceleration is constant, the average acceleration is also the same as the instantaneous acceleration. From the definition of acceleration we have
![]()
Multiplying both sides by t and solving for v.
![]()
Thus we see that ![]() and
and ![]() are equivalent when the acceleration is constant.
are equivalent when the acceleration is constant.
Calculus Derivation:
Start with the definition of instantaneous acceleration and multiply both sides by the differential dt.
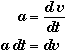
Next integrate both sides.
![]()
Since the acceleration is constant and can be taken out from inside the integral over time
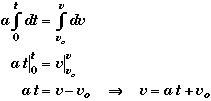
Derivation of
![]()
Analytical Geometry Derivation:
In analytical geometry it can be shown that the average value of a straight line is the arithmetic average of its end points. The plot of the velocity versus time of an object undergoing a constant acceleration is a straight line.
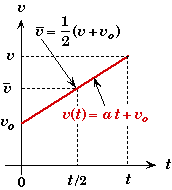
![]()
Given the definition of average velocity, and the fact that the average velocity is the arithmetic average of the initial and final velocities, we find
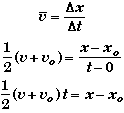
The average velocity can only be expressed as an arithmetic average of initial and final velocities when the acceleration is constant. It is not true in general.
Note that the average location of an accelerating object is not half way between the starting and ending locations.
![]()
An objects spends a lot more time in the first half of its distance interval than in the last half because it is going slower in the first half than in the last half. However, if the object is moving at a constant speed, then the average location is at the midpoint of its motion since the object's location is a linear function of time.
Calculus Derivation:
For constant acceleration
![]()
We can evaluate the time average of the velocity directly since we know the velocity function's time dependence.
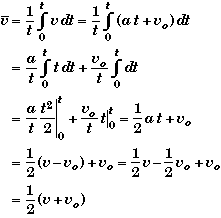
Derivation of
![]()
Algebraic Derivation:
Starting with
![]()
and substituting
![]()
we find
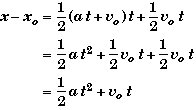
Calculus Derivation:
Start with the definition of instantaneous velocity.
![]()
Next multiply both sides by the differential dt and integrate.
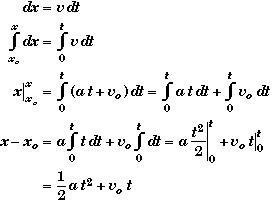
Derivation of
![]()
Start with
![]()
Solve
![]()
for time and substitute it into the distance equation to eliminate the time.
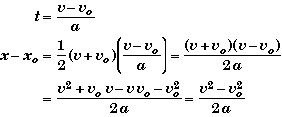
Source: http://physics.mtsac.edu/4A/4A%20Text/Kinematics.doc
Web site link: http://physics.mtsac.edu/
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Kinematics notes
Kinematics notes
Kinematics notes
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Kinematics notes mean ? Which is the meaning of Kinematics notes?
Kinematics notes physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us