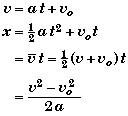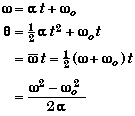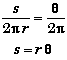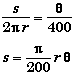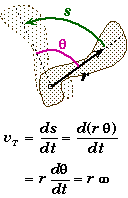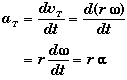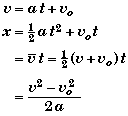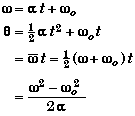Rotational kinematics
Rotational kinematics
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Rotational kinematics
Rotational Kinematics:
LINEAR |
Connection |
ROTATIONAL |
Position |
s = r q |
Angle |
Velocity |
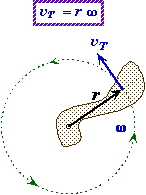
vT = r w |
Angular Velocity |
Acceleration |
Tangential |
ANGULAR MEASUREMENT
Angleq : Orientation of an object relative to some fixed axis.
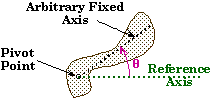
- The angle q measures the state of rotation of an object at a given moment.
- For a rotating object, q will change with time.
Units |
A circle divided into |
|
Degrees: |
360 equally spaced units. |
|
Radians: |
2p equally spaced units. |
|
Grads: |
400 equally spaced units. |
Degrees (o) |
SI: Radians (rad) |
Grads |
1 rev = 360o |
1 rev = 2p rad |
1 rev = 400 grads |
- The unit "radian" is not really a true unit. It is a marker that specifies how a circle will be divided up. Often you will need to drop "rad" in equations that relate linear and rotational quantities, such as s = rq. Otherwise, you would have that "m = m . rad" which is impossible if "rad" stood for a unit.
Angular Velocity
The angular rate at which a rigid object is rotating.
Definition:
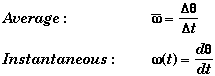
- Every point on a rotating body has the same angular velocity even though every point does not have the same linear velocity. This is what makes the angular velocity a useful measure of the rate of rotation.
Units:
SI: rad/s
Others Units: rev/s, rpm = rev/min, deg/sec
Tangential Velocity:
* The linear velocity of a point on a rotating rigid object at a distance r from the axis of rotation represents the tangential velocity of that point.
 |
|
* For rotation about a fixed pivot point, the path of any point on a revolving body is a circle, and its linear velocity at any moment is always tangent to that circle.
Angular Acceleration:
Measures how fast an object's rate of rotation is speeding up or slowing down.
Definition:
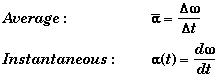
* The angular acceleration of all parts of a rotating body is the same, independent of how close or how far each part is from the axis of rotation.
Units:
SI: rad/s2
Others Units: rev/s2, deg/sec/sec
Tangential Acceleration:
The linear acceleration of a point on a rotating object at a distance r from the axis of rotation .
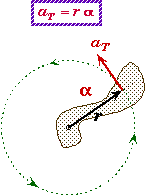 |
|
- For freely rotating object, each point could have both a tangential and radial acceleration.
Uniform or Constant Angular Acceleration
- The equations for constant angular acceleration acceleration have the same structure as the equations for constant linear accelaeration.
- Only the symbols are different. Greek letters are used to indicate that one is talking about rotational motion as opposed to linear motion.
Linear Equation |
Angular Equations |
a = constant |
a = constant |
- If you know the linear equations you can determine the rotational equations using the mapping
x => q |
v => w |
a => a |
- It is important to use greek symbols for rotational quantities because there are many problems that have both linear and rotational motion at same time.
Uniform Circular Motion:
* When an object moves in a circle at a constant speed, it is said to undergo uniform circular motion.
* The time it takes the object to make one revolution is called the object's period P. If the object is moving at a constant speed, then
![]()
* For uniform rotational motion, the angle the object makes with the x-axis is simply ![]() provided that at time zero the object is on the x-axis. Here w is the angular velocity of the object's rotation about the center, and is equal to either: w = v/r or w = 2p/P
provided that at time zero the object is on the x-axis. Here w is the angular velocity of the object's rotation about the center, and is equal to either: w = v/r or w = 2p/P
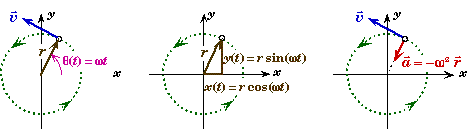
* The object's location at any moment - its equation of motion - relative to the center of rotation is given by
![]()
where i and j with the little hats are the unit vectors in the x and y directions.
* The object's velocity is easily found by taking the derivative of its location with respect to time.
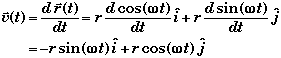
* This velocity is always tangent to the circle or equivalently, ![]() is always perpendicular to
is always perpendicular to ![]()
![]()
* The object's acceleration is easily found by taking the derivative of its velocity with respect to time.
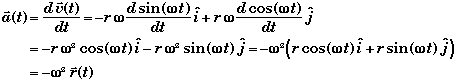
* The direction of the object's acceleration ![]() is opposite
is opposite ![]() , i.e.,
, i.e., ![]() directed towards the center of motion.
directed towards the center of motion.
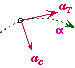
Centripetal Force and Acceleration:
Centripetal Acceleration:
- In order for an object to execute circular motion - even at a constant speed - the object must be accelerating towards the center of rotation. This acceleration is called the centripetal or radial acceleration and has a magnitude of
![]()
ac |
= Centripetal acceleration |
SI: m/s2 |
vT |
= Tangential velocity or speed |
SI: m/s |
r |
= Radius of object's path |
SI: m |
w |
= Angular velocity |
SI: rad/s |
Centripetal Force:
- The radial force needed to create this acceleration is call the centripetal force. It is directed towards the center of rotation and has a magnitude of
![]()
- For any object undergoing uniform circular motion, the net force towards the center of rotation must have a value equal the centripetal force.
Centrifugal Force:
- In a frame of reference rotating with an angular velocity w (omega), the object will be at rest, yet seem to experience a force acting upon it radially outwards equal to m w2r. This is because a rotating frame is a non-inertial frame of reference, i.e. the frame does not move at a constant speed in a straight line, and consequently Newton's First Law does not apply.
- It is sometimes useful to move into a frame that is rotating with the system. In this rotating frame, the centripetal force is replaced with a force of the same magnitude acting outwards, which is called the centrifugal force. ("Centrifugal" means "fleeing from the center.") In solving a problem in the rotating frame, the centrifugal force can be treated as though it were another physical force acting on the object with a magnitude m w2r (the same magnitude as the centripetal force) directed radially outwards. Most physicists would advise against doing this, because the centrifugal force is not a real force. I still find it useful in visualizing a problem.
Conical Pendulum Problem
A 1.50 kg bob swings in a horizontal circle from a 50.0 cm cord which is attached to the ceiling. The bob moves at a constant speed in such a way that the cord makes an angle of 62.0O with the ceiling. |
||
What is the tension in the cord ? |
|
|
What is the magnitude of the centripetal force ? |
||
What is the bob's angular velocity and linear velocity ? |
||
What is the bob's period ? |
||
Sketch and Process:
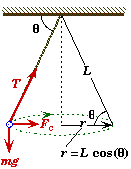
A object moves in a horizontal circle at a uniform speed.
Givens and Labels:
m |
= 1.50 kg |
|
(Mass of the bob) |
L |
= .500 m |
|
(Length of the cord) |
q |
= 62.0o |
|
(Angle cord makes with the ceiling) |
r |
= ? |
|
(Radius of the bob's circular motion) |
T |
= ? |
|
(Tension in the cord) |
Fc |
= ? |
|
(Centripetal force) |
Relevant Physics:
Newton's 2nd Law can be applied the bob.
-The net force in the vertical direction must be zero since the bob does not move up or down.
-Since the bob is going in a circle with uniform speed, the net radial force has to be equal to the centripetal force.
![]()
A free-body diagram of the forces acting on the bob is useful in picturing the action of the forces acting on the bob and in determining the radius of the circular motion.
Vertical Forces:
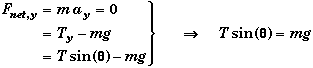
Radial Forces:
![]()
Note that in the diagram as it is drawn, Tr is the same as Tx. However, this is only true at this moment. Since the motion is radial, Tr is a more accurate description of the Force's direction.
(A) Find the tension in the cordT.
From the balance of the vertical forces, we see that vertical component of the tension must be equal to the weight of the bob.

(B) Find the magnitude of the centripetal force Fc.
The only radial force acting on the bob is the horizontal component of the tension in the cord, so Tx must be equal to the centripetal force.
![]()
Symbolic Solution:
From the vertical-force equation we have,
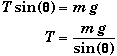
Placing this into the radial force equation and solving for Fc
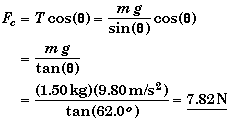
(C) Find the bob's angular velocity w and linear velocity vT.
We have already found the numerical value of the centripetal force in part B, so we can use the equation for the centripetal force to find w. Using geometry, we can find the radius of the bob's orbit as a function of the parameters given, namely the length of the cord and its angle.
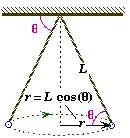
![]()
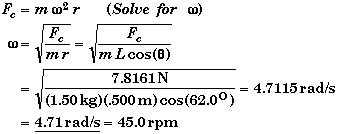
and the tangential velocity is,
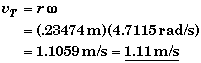
Symbolic Solution:
From the radial-force equation we have,
![]()
From the vertical-force equation we have,

Since the mass has canceled out, the angular velocity does not depend upon the mass of the bob, but only upon the length of the cord and the angle it makes with the ceiling. The tension in the cord depends upon the mass of the bob, but surprisingly not upon the length of the cord, only its angle.
(D) Find the period of the bob t .
The bob will make one revolution when it has gone through a horizontal angle of 2p. Thus,![]()
Rolling Without Slipping:
* If an object rolls without slipping, then the bottom of the rolling object (at the point of contact) must be momentarily at rest relative to a fixed observer.
* Rolling without slipping can be thought of as the motion of the center of mass (fixed observer) plus rotational motion about its center of mass (observer moving with the object).
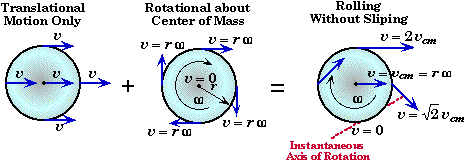
* In the case for rolling without slipping, the distance, the velocity, and the acceleration of the center of mass is directly related to the angle of rotation, the angular velocity, and the angular acceleration about the center of mass.
![]()
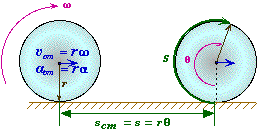
Slipping and Rolling Disk
A disk on a horizontal surface is made to slip by a applied horizontal force. Friction between the surface and the disk eventually causes the disk to roll without slipping. When the disk rolls without slipping you can observe that the velocity of the center of mass is equal to the velocity of the rim of the disk.
Total Mechanical Energy for Linear and Rotational Motion of a Solid:
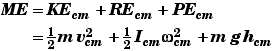
The total mechanical energy of an object is equal to the kinetic energy of its center of mass plus the rotational energy about its center of mass plus the gravitational potential energy of it center of mass.
Free Rotational Dynamics:
* The Overall Motion of a Rigid Object can be split into Linear Motion of its Center of Mass plus its Rotational Motion about its Center of Mass.
* Free rotational motion is equivalent to the dynamics of an object rotating about a fixed axis (the cm) when you are moving along with the cm. In this moving frame, the center of mass becomes the pivot point for the fixed axis of rotation.
Equation that apply to a freely rotating object
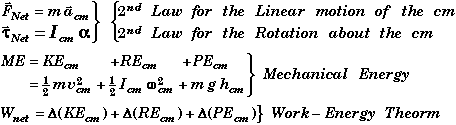 |
Rotation About a Fixed Axis:
* For a Rigid Object rotating about a Fixed Axis, the Overall Motion of the object can be treated as though it is Purely Rotational Motion about the fixed axis of rotation, the pivot point.

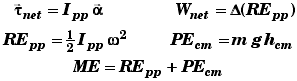
Rotational Energy |
|
* Energy due to an object's state of rotational motion.
* The minimum Work needed to get an object with a moment of inertia I rotating at an angular velocity w - starting from rest.
Gold Block on Accelerating Turntable Problem
A 2.30 kg gold block rests on the surface of a horizontal turntable, 65.0 cm from the center. The coefficient of static friction between the gold block and the turntable's surface is .440. The turntable starts from rest and is given a uniform angular acceleration of 1.80 rad/s2. |
|
(A) |
What are the tangential and radial accelerations of the gold block 1.10 seconds after the turntable starts accelerating ? |
(B) |
What is the magnitude and direction of the force of friction acting on the gold block 1.10 seconds after the turntable starts accelerating ? |
(C) |
How long after the turntable starts accelerating will it take for the gold block to start slipping ? |
Sketch and Process:

A turntable has a constant angular acceleration starting from rest. A gold block resting on the surface of the turntable is set into motion along with the turntable due to the friction between the block and the turntable.
Givens and Labels:
m |
= 2.30 kg |
(Mass of the gold block) |
r |
= .650 m |
(Distance of block from center of rotation) |
ms |
= .440 |
(Coefficient of static friction) |
a |
= 1.80 rad/s2 |
(Angular acceleration of the table) |
at |
= ? |
(Tangential acceleration of the gold block) |
ac |
= ? |
(Radial or centripetal acceleration of the block) |
b |
= ? |
(Angle of acceleration relative to moving frame) |
Ft |
= ? |
(Tangential force on the gold block) |
Fc |
= ? |
(Radial centripetal force on the gold block) |
ax |
= ? |
(x-component of the acceleration) |
ay |
= ? |
(y-component of the acceleration) |
q |
= ? |
(Angle of acceleration relative to x-axis) |
f |
= ? |
(Angle through which disk rotates relative to x-axis) |
Relevant Physics:
The radial and tangential directions are independent of each other since they are at 90o to each other. Consequentially the motion of any object moving in a circle can be broken up into two parts, the tangential motion and the radial motion. After solving these two parts separately they can be combined vectorially to determine the block's total motion in the x-y -plane. This process is similar to what we did in studying projectile motion, only now the frame is rotating.
The only force (besides gravity) acting on the gold block is the static force of friction f. The direction of the friction on the block can be resolved into both a radial component fr and a tangential component ft. These two components are directly related to the block's centripetal and tangential accelerations.
Tangential Motion:
The block is undergoing a constant angular acceleration, with a constant tangential acceleration.
![]()
Radial Motion:
To move in a circle, the block must have an inward radial acceleration equal to the centripetal acceleration,
![]()
We choose the inward direction to be positive in our co-rotating coordinate frame so that the sign of the term w2r will be positive which indicates that the centripetal acceleration is towards the center. Since w is increasing with time, the radial acceleration will also increase with time.
(A) Find at and ac when t = 1.10 s.
The tangential acceleration does not depend upon time since the angular acceleration is constant.
![]()
Since wo = 0, at 1.10 s:
![]()
and the centripetal (or radial) acceleration is given by
![]()
(B) Find magnitude and direction of the force on the block at 1.10 s.
Since the only force acting on the gold block is the force of static friction f, the net force on the block must be equal to the force of friction. Applying Newton's Second Law to the two independent components - the tangential acceleration and centripetal acceleration - we have,

Alternately we could have just found the magnitude of the block's acceleration at this moment and multiplied it by the block's mass.
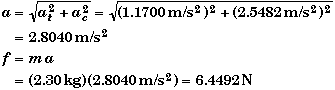
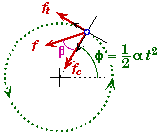 Finding the direction is more complicated. Although we know the magnitude of the centripetal and tangential acceleration, their directions depend upon the angle f through which the disk (and block) have turned. Since the disk's angular acceleration is constant and the disk starts from rest we can easily find f.
Finding the direction is more complicated. Although we know the magnitude of the centripetal and tangential acceleration, their directions depend upon the angle f through which the disk (and block) have turned. Since the disk's angular acceleration is constant and the disk starts from rest we can easily find f.

Now ac (or fc ) is along this angle but towards the origin. Thus the direction of ac is f + 1800. Since at (or ft ) is at 900 to f, its direction is f + 900. Using this information we could resolve both ac and at into x- and y- components and add them up to determine the total magnitude and direction of the block's acceleration (or force).
A slightly shorter and more intuitive method is to consider the meaning of the angle b found from the radial and tangential components.
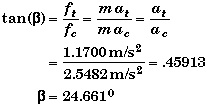
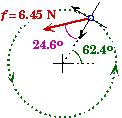
We could just state this value as an acceptable answer as asked in the problem. The force is 24.70 from the radius vector towards the center of the disk.
If we were explicitly asked to find the direction q relative to the x-axis, we would need to use some geometry to find q knowing f and b. First observe that the angle is pointing into the fourth quadrant so that,
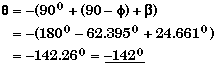

(C) Find the time t when the gold block starts to slip.
The magnitude of the maximum value that static friction can exert on the block is given by
![]()
At the moment just before the block starts to slip, this will be the value of the net force acting on the block,
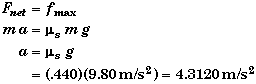
We see that the time required for the block to start slipping will not depend upon the mass of the block. The block will slip when the magnitude of the block's linear acceleration becomes greater than 4.312 m/s2. Putting a heavier gold block on the table will not increase the time for the gold block to begin slipping.
To find the time, we equate this value for the acceleration with the magnitude of the acceleration derived from its radial and tangential components, and solve for time.
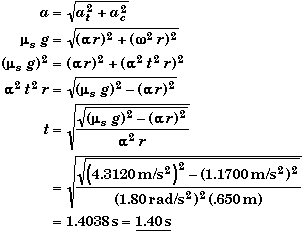
Rolling Marble Problem
A solid marble with a radius of 2.60 cm and a mass of 370 grams is rolling along the ridge of a hill that is 58.0 cm high. Initially the sphere is observed to revolve 15 times every second just before it encounters a downhill section. If the marble rolls without slipping, and the energy lost due to rolling friction is negligible: |
|
(A) |
What is the sphere's initial mechanical energy ? Initially, what fraction of the sphere's mechanical energy is potential energy, kinetic energy, and rotational energy ? |
(B) |
Show that the ratio of the marble's kinetic energy to its rotational energy is constant throughout its motion. |
(C) |
What is the maximum height that the marble could roll up an elevated section ? |
(D) |
How fast will the marble be moving when it reaches the bottom of the hill ? |
Sketch and Process:
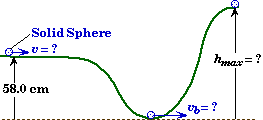
A marble rolls without slipping along an undulating surface.
Givens and Labels:
m |
= .370 kg |
(Mass of the marble) |
r |
= .0260 m |
(Radius of the marble) |
wo |
= 15 rev/s |
(Initial rotation of the marble) |
ho |
= .580 m |
(Initial height of the marble) |
vo |
= ? |
(Initial velocity of marble) |
hmax |
= ? |
(Maximum height of marble) |
vb |
= ? |
(Velocity at bottom of slope) |
Relevant Physics:
For a freely rotating body the total mechanical energy is conserved.

This means that if we can find the mechanical energy at some point along the marble's path, then we know the marble's ME at all other points along its path. Since we know something about the marble's initial motion and position, we can find the initial ME.
Since the marble is rolling without slipping, then its angular velocity is related to the linear velocity of its center of mass,
![]()
(A) Find MEo.
We really do not need a separate symbol to distinguish the marble's initial mechanical energy MEo from the ME at any other point, since the mechanical energy is energy is conserved.
![]()
To determine the KEo we need to determine the marble's initial velocity. Since the marble's velocity is just the velocity of its center of mass, and the ball is rolling without slipping,
![]()
Then
![]()
To determine the REo we need to determine the marble's moment of inertia I. Since the marble is a solid sphere,
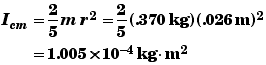
Then
![]()
We already have the value of all the quantities we need to determine PEo relative to its position when it is at the bottom of the hill. We do not need to worry about the fact that the center of mass of the ball is 2.60 cm above the track since the center of mass is also 2.60 cm above the track at the bottom or any place else along the track.
![]()
The total energy is the sum of the kinetic, potential, and rotational energy.
![]()
The fraction of mechanical energy that is KE, RE, and PE is simply their ratio.
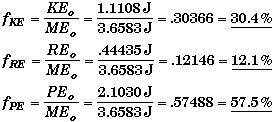
(B) Find KE / RE at any point.
Since the marble is rolling without slipping, then v = w t at any point.
![]()
For any object that rolls without slipping there is a fixed ratio between the KE and the RE , because there is a fixed relationship between the object's linear speed and its angular speed.
The ratio of the KE to PE will not be constant, since the ball's velocity and height are not necessarily related.
(C) Find hmax.
When the ball reaches its highest point, it will come to a halt and stop rolling. All of its ME will be PE. At its highest point,
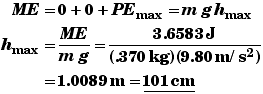
An alternate symbolic solution is,

Thus the maximum height does not depend upon the mass of the marble. A marble of any mass which has the same radius would go to the same height under the same starting conditions. This means that this part of the problem could have been stated without specifying the marble's mass. If the mass was not given then you would have to solve the problem symbolically to find hmax.
(D) Find vb , the velocity of the marble at the bottom.
At the bottom the marble's PE is zero since we chose this level as our reference frame. The marble has both KE and RE at the bottom, the sum of which will be equal to the marble's ME.
![]()
Since the marble is rolling without slipping, vb = wb r.
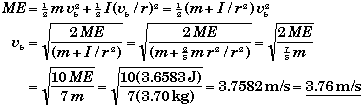
Rotational Calculus Relations:
The variables that describe rotational motion are related by a set of integral calculus relations similar to those for linear variables.
Variable |
Derivative Relationships |
Integral Relatiomships |
Angular Position |
|
|
|
|
|
|
|
|
|
|
|
Angular Acceleration |
|
|
Rotational Kinematic Problem-Solving:
What point is the system rotating around ?
* The radius vector rused in the rotational equations is the distance from the axis of rotation and not necessarily the radius of the object.
* For free rotational motion r is the distance to the center of mass since this the point about which the object will rotate.
Is the rotational acceleration a of the system constant or zero ?
* If the angular acceleration is constant then you can use rotational kinematic equations.
* Many of the points you must consider are similar to those you used in solving linear kinematics problem.
* Most rotational problems have a linear analogy. When first learning how to solve rotational problems, it is useful to consider the linear counterpart since you may be more familiar with it. For example, a rotating turntable that slows to a stop is equivalent to a moving block sliding to a halt.
* The structural form of the rotational kinematic equations is similar to the form of the linear kinematic equations. Only the symbols have changed,
x => q |
v => w |
a => a |
* Do not be afraid to use Greek symbols. The advantage is that if you see a Greek symbol, you know it indicates a rotational quantity and not a linear quantity. Just because you may not be familiar with using Greek symbols does not mean you should avoid their use. The structure of any symbol is not what is important, it is what concept the symbol points to that is important.
Do I have the values of all the angular variables in radians ?
* Most equations that relate linear and rotational quantities such as v = w r, will not work correctly unless the angular quantities are expressed in terms of radians.
* A purely rotational equation such as 2aq = w2- wo2 can be expressed in degrees or revolutions, provided you use the same units consistently for every term in every rotation equation you use. You cannot have w in rev/s, q in degrees, and a in rad/s2 in the same equation or in two equations that are related. It is a lot easier to convert all the variables given to radians /something at the beginning of a problem and be done with it.
Source : http://physics.mtsac.edu/4A/4A%20Text/RotationalKinematics.doc
Web site link: http://physics.mtsac.edu
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Rotational kinematics
Rotational kinematics
Rotational kinematics
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Rotational kinematics mean ? Which is the meaning of Rotational kinematics?
Rotational kinematics physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us