Lenses
Lenses
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Lenses
Two types of spherical lens: concave (caves in as you look at it – also known as converging) and convex (diverging)
Convex (converging) lenses – ray diagrams
You should be able to draw a ray diagram showing how an image is formed by a convex lens when the object is placed
- outside the focus – resulting in a real image
- inside the focus – resulting in a virtual image
Three Rules
From top of object to lens (parallel to principle axis) and after passing through the lens then passes through the focal point on the other side.
From top of object through focal point and after passing through the lens continues on the other side parallel to the principle axis.
Centre of Curvature: From top of object to centre of curvature and continues straight through.
For each of the following label the focal point, the object and the image.
Put arrows on all rays, and state whether the image is real or virtual, upright or inverted, magnified or diminished
Object outside f Object inside f
Notice that when the object is inside the focal point the light rays never intersect, but from the viewer’s perspective they appear to do so behind the mirror (the viewer is to the right of the lens in the diagrams above).
Note
A real image is always on the other side of the lens (to the object) and is inverted.
A virtual image is always on the same side of the lens is upright.
Concave (diverging) lenses – ray diagrams
Here only one diagram is needed; the image is always diminished, upright and virtual.
Two Rules
- From top of object to the lens parallel to principle axis and up as if coming from the focal point.
- From top of object to the lens as if passing through centre of curvature.
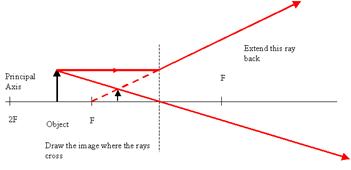
Notice that in this situation (similar to the convex mirror when the object is inside the focus) light rays never intersect, but from the viewer’s perspective they appear to do so at the same side of the lens as the mirror.
The image is therefore always virtual, regardless of where the object is placed.
Maths Problems
Relationship between focal length (f), object distance (u) and image distance (v)
Convention:
For a convex lens f is positive
For a concave lens f is negative
For a real image v is positive
For a virtual image v is negative
The last two lines are what is referred to as the ‘Real is Positive’ convention (RiP).
Remember that for a convex lens the image is only virtual if the object is inside the focus.
For a concave lens the image is always virtual.
u is always positive for both types of lens
Magnification
If you are told that v is virtual, or if it is obvious from the question (because the lens is diverging or because the object is inside the focal length if the lens is converging) then you should make the value for v negative at the beginning of the question.
See problems 1- 3, pages 46, 47, followed by questions 1 – 7, page 48.
Remember that for a convex lens f is always negative, and because the image is always virtual, so is v.
See problems 4 and 5; then try questions 1- 4, page 51.
Question 4 looks a little unusual, but try answering it in the normal fashion.
Note: If you are told that v is virtual, or if it is obvious from the question (because the lens is concave, or because the object is inside the focal length if the lens is convex) then you should make the value for v negative.
Power of a Lens*
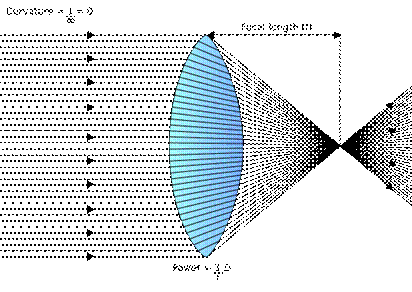
Power of a Lens = 1/focal length
The unit of power is m-1.
Convention
The power of a converging (convex) lens is taken as positive (+) {because f is positive}.
The power of a diverging (concave) lens is taken as negative (-) {because f is negative}.
Two Lenses in Contact
If two lenses of power P1 and P2 are placed in contact, the power P of the combination is given by
PTotal = P1 + P2
Remember to use the correct sign notation.
It follows from this that if two lenses of focal length f 1 and f2 are placed in contact, the focal length f of the combination is given by
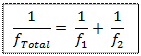
Remember to use the correct sign notation.
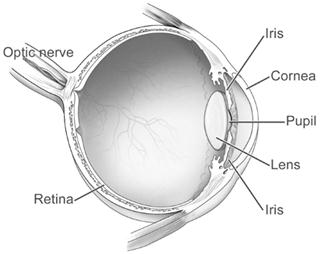
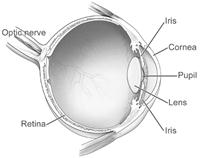
The Eye*
Retina - light sensitive screen at the back of the eye,
Optic Nerve – carries the information in electrical form to the brain
Cornea – together with The Lens, form part of the focusing system.
Iris – acts like a shutter to control the amount of light entering the eye
Power of Accommodation
The Power of Accommodation of the eye is its ability to focus a real image of an object on the retina, whether the object is near to or far away from your eye.
Defects of Vision; short and long-sightedness
Short Sight
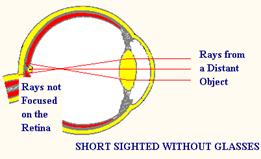
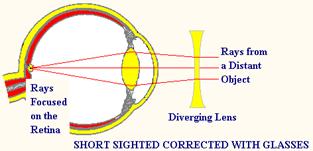A Short-sighted person can see nearby objects clearly but cannot bring distant objects into focus.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
- - - - - - - - - - - - - - - - - - - - - - - - - - - -- - - - - - - - - -
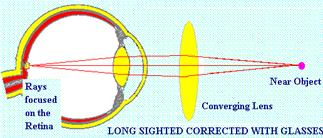
Long Sight
A Long-Sighted person can see distant objects clearly but cannot bring nearby objects into focus.
Leaving Cert Physics syllabus: Lenses
Content |
Depth of Treatment |
Activities |
STS |
|
|
|
|
Lenses |
Images formed by single thin lenses. |
Simple exercises on lenses by ray tracing or use of formula. |
Use of lenses |
|
|
|
|
|
m = v/u |
|
|
|
|
|
|
|
Power of lens: P = 1/f |
|
|
|
|
|
|
|
Two lenses in contact: |
|
|
|
|
|
|
|
The eye: Optical structure, short sight, long sight, and corrections. |
|
Spectacles |
|
|
|
|
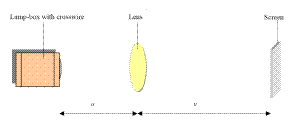
MEASUREMENT OF THE FOCAL LENGTH OF A CONVEX LENS
APPARATUS
Converging lens, screen, lamp-box with crosswire, metre stick, retort stand.
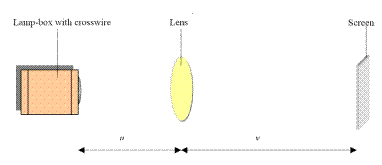DIAGRAM
PROCEDURE
- Place the ray-box well outside the approximate focal length.
- Move the screen until a clear inverted image of the crosswire is obtained.
- Measure the distance u from the crosswire to the lens, using the metre stick.
- Measure the distance v from the screen to the lens.
- Repeat this procedure for different values of u.
- Calculate the focal length of the lens each time using the formula
and get an average. - Plot a graph of 1/u against 1/v and use the intercepts to get two values for f. Then get the average of these two.
RESULTS
Object distance u |
|
|
|
|
|
|
1/u |
|
|
|
|
|
|
Image distance v |
|
|
|
|
|
|
1/v |
|
|
|
|
|
|
|
|
|
|
|
|
|
Focal Length f |
|
|
|
|
|
|
CONCLUSION
Using the graph we got an average value for the focal length of the lens of 25.6 cm.
From the table of data we got an average value of 24.4 cm, which was close to the value we got from the graph, suggesting that both readings are reasonably accurate.
SOURCES OF ERROR / PRECAUTIONS
- Determining when the image was in sharpest focus; repeat each time and get an average.
- Parallax error associated with measuring u and v; ensure your line of sight is at right angles to the metre stick.
- Take all measurements from the centre of the lens.
NOTES
How to find an approximate value for the focal length.
- Focus the image of a distant object onto a screen.
- Measure the distance between the lens and the screen.
- This corresponds to an approximate value for the focal length of the lens.
Using the graph to calculate the focal length
It is also possible to draw a graph, on graph paper, of 1/v (y-axis) against 1/u.
The equation of the line can be compared to the standard form of linear equation, y = mx + c.
In this case it is: 1/v = -1/u + 1/f. This cuts (intercepts) the y-axis (1/v axis) when x (1/u) is zero i.e. 1/v = 0 + 1/f. Similarly the line intercepts the 1/u axis when 1/v is zero, giving us 1/u = 1/f.
From your graph get the average of the two intercepts, find the reciprocal to get the value of f.
Extra Credit
Confusion with Mirrors and Lenses
Whereas a concave mirror gives a real image (unless the object was inside the focus) this time it’s a convex lens which gives a real image (unless the object is inside the focus) and a concave lens always gives a virtual image.
Secondly, whereas with mirrors a virtual image was always formed behind the mirror, with lenses it’s a real image which is formed at the other side of the lens, and a virtual image is always formed on the same side of the lens as the object.
After that however the chapter is remarkably similar to the chapter on spherical mirrors.
Why are you advised not to water plants on a bright sunny day?
The water forms droplets on the leaves. Thesedroplets act as converging lenses and focus thesun onto the leaves, burning them. As a result theleaves will have brown spots.
*Power of a lens
The power of a lens is defined as the reciprocal of the focal length in metres. The unit of power is the m–1. Opticians use the dioptre as the name of the unit of power but this is not used in the SI system.
*The Eye
Did you know that a TV screen shows 24 pictures a second? Because a fly sees 200 images a second, it would see TV as still pictures with darkness in between.
Why can we not focus clearly under water yet swimming goggles will restore clear focus?
Light refracts when travelling from air through the cornea of your eye, but water and the cornea have the same refractive index (not surprising I suppose – the cornea seems to be mostly water) so light which travels from water to your cornea doesn’t refract much at all, so there is no focusing on the retina.
By wearing goggles however light which hits your eye is coming from air, so the usual focusing applies and objects appear normal. Unless you happen to be on a family holiday in Majorca and find yourself underwater staring at Granny’s cellulite arse, in which case ‘normal’ is not the word which first comes to mind.
Physics, Art and History
Focus an image of a distant object on a screen (a white page) using lenses or mirrors. This is always impressive, particularly when you notice that the image is in colour, and upside down.
The lenses must be convex (converging), and the mirrors concave. Why?
Some historians of art now believe that from the early 15th century many Western artists including Van Eyck, Caravaggio and Vermeer used mirrors and lenses to create living projections.
Optics would have given artists a new tool with which to make images that were both immediate and powerful, enabling them to project colour images onto flat surfaces and then capture these projections in pencil and paint.
Upside down glasses
The upside-down glasses were first investigated by George Stratton in the 1890’s. Since the image that the retina of our eye sees is inverted, he wanted to explore the effect of presenting to the retina an upright image. He reported several experiments with a lens system that inverted images both vertically and horizontally. He initially wore the glasses over both eyes but found it too stressful, so he decided to wear a special reversing telescope over one eye and keep the other one covered.
In his first experiment, he wore the reversing telescope for twenty-one hours. However his world only occasionally looked normal so he ran another experiment where he wore it for eight days in a row. On the fourth day, things seemed to be upright rather than inverted. On the fifth day, he was able to walk around his house fairly normally but he found that if he looked at objects very carefully, they again seemed to be inverted. On the whole, Stratton reported that his environment never really felt normal especially his body parts, although it was difficult to describe exactly how he felt. He also found that after removing the reversing lenses, it took several hours for his vision to return to normal.
Three sons bought a farm and named it ‘The Focal Point’. When their father asked why they chose that name, they replied, “It’s the place where the sons raise meat”.
(Think about it)
Physics exam questions
- [2006]
A converging lens is used as a magnifying glass.
Draw a ray diagram to show how an erect image is formed by a magnifying glass.
- [2006]
A diverging lens cannot be used as a magnifying glass. Explain why.
- [2006]
A converging lens has a focal length of 8 cm.
Determine the two positions that an object can be placed to produce an image that is four times the size of the object?
- [2008 OL]
A concave lens has a power of 0.1 cm−1. What is the focal length of the lens?
- [2002 OL]
A lens has a power of +50 m-1. What type of lens is it and what is its focal length?
- [2004]
Two converging lenses, each with a focal length of 10 cm, are placed in contact. What is the power of the lens combination?
- [2002]
- The power of a normal eye is +60 m-1. A short-sighted person’s eye has a power of +65 m-1.
Calculate the power of the contact lens required to correct the person’s short-sightedness.
- Calculate the focal length of the contact lens required to correct the person’s short-sightedness.
- [2006]
The power of an eye when looking at a distant object should be 60 m–1. A person with defective vision has a minimum power of 64 m–1.
(i) Calculate the focal length of the lens required to correct this defect.
(ii) What type of lens is used?
(iii) Name the defect.
- [2002]
Draw a labelled diagram showing the optical structure of the eye.
- [2002]
How does the eye bring objects at different distances into focus?
- [2008]
- An eye contains a lens system and a retina, which is 2.0 cm from the lens system. The lens system consists of the cornea, which acts as a fixed lens of power 38 m–1, and a variable internal lens just behind the cornea. The maximum power of the eye is 64 m–1.
Calculate how near an object can be placed in front of the eye and still be in focus.
- Calculate the maximum power of the internal lens.
- Light is refracted as it enters the cornea from air as shown in the diagram.
Calculate the refractive index of the cornea.
- Draw a diagram to show th path of a ray of light as it passes from water of refractive index 1.33 into the cornea.
- A swimmer cannot see properly when she opens her eyes underwater.
When underwater why does the cornea not act as a lens?
- What is the maximum power of the eye when underwater?
- Why do objects appear blurred when underwater?
- Explain how wearing goggles allows objects to be seen clearly.
Mandatory Experiment
- [2005 OL]
You carried out an experiment to measure the focal length of a converging lens.
- Draw a labelled diagram of the apparatus that you used in the experiment.
- Describe how you found the position of the image formed by the lens.
- What measurements did you take?
- How did you get a value for the focal length of the converging lens from your measurements?
- Give one precaution that you took to get an accurate result.
- [2009]
A student was asked to measure the focal length of a converging lens. The student measured the image distance v for each of three different object distances u. The student recorded the following data.
u/cm |
20.0 |
30.0 |
40.0 |
v/cm |
65.2 |
33.3 |
25.1 |
- Describe how the image distance was measured.
- Give two precautions that should be taken when measuring the image distance.
- Use all of the data to calculate the focal length of the converging lens.
- What difficulty would arise if the student placed the object 10 cm from the lens?
- [2003]
The following is part of a student’s report of an experiment to measure the focal length of a converging lens.
“I found the approximate focal length of the lens to be 15 cm.
I then placed an object at different positions in front of the lens so that a real image was formed in each case.”
The table shows the measurements recorded by the student for the object distance u and the image distance v.
u/cm |
20.0 |
25.0 |
35.0 |
45.0 |
v/cm |
66.4 |
40.6 |
27.6 |
23.2 |
- How did the student find an approximate value for the focal length of the lens?
- Describe, with the aid of a labelled diagram, how the student found the position of the image.
- Using the data in the table, find an average value for the focal length of the lens.
- Give two sources of error in measuring the image distance and state how one of these errors can be reduced.
Exam solutions
Object inside focal point
Two (appropriate) rays from object to lens
Two rays emerge correctly from lens
Rays produced back to form upright virtual image (on same side as object)
- The image is always diminished.
- 1/u + 1/v = 1/f
Magnification = v /u = 4 Þ v = 4u
For real image: 1/u + 1/4u = 1/8 Þ u = 10 cm
For virtual image: 1 /u - 1/4u = 1/8 Þ u = 6 cm
- P = 1/f Þ f = 1/P = 10 cm.
- P = 1/f Þ f = 1/P Þ f = .02 m. It is a converging (convex) lens.
- P1 = 1/f1 = 10 m−1 , P2 = 1/f2 = 10 m−1
P = P1 + P2 = 20 m-1
- (i) PTotal = P1 + P2
60 = 65 + P2
Power = - 5 m
(ii)P = 1/f Þ f = - 0.2 m
- (i) P = P1 + P2 Þ 60 = 64 + P2 Þ P2 = -4 ( m-1)
P = 1/f Þ f = 1/P Þ 1/f = (-)4 Þ f = (-)¼ m = (-)25 cm
(ii) Diverging / concave lens
(iii) Short sight / myopia
- See diagram.
- It can change the shape of the lens which in turn changes the focal length of the lens.
- Pmax = 64 m-1 = 1/f
f = 0.0156 m = 1.56 cm
1/u = 1/v +1/f Þ 1/u = 1/2 = 1/1.56 Þ u = 7.14 cm
- Pmax = P1 + P2 Þ 64 = 38 + P2 Þ P2 = 26 m-1
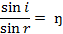
Þ n = sin 37/sin 27 Þ n = 1.33
- Both media have the same refractive index so there is no bending of light.
Draw a straight line passing from one medium to the other without bending.
- Because light does not refract at the cornea since there is no change in refractive index.
- The maximum power of the eye is 64 m–1, but this includes the focusing power of the cornea (38 m-1) which doesn’t work underwater, so maximum power = 64 – 38 = 26 m–1.
- Because the internal lens by itself is not powerful enough to focus light on retina.
- Because light which hits the cornea is coming from air and so there will be refraction here (the cornea will now act as a lens).
Mandatory Experiment
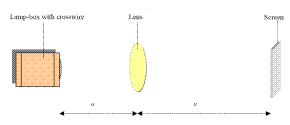
- See diagram. Include a metre-stick.
- We kept the ray-box and the lens fixed and moved the screen until there was a clear image formed on the screen.
- We measured the distance from object (cross-wires) to the lens (u) and the distance from the lens to the screen (v).
- By substituting the values for u and v into the formula
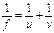. - Ensure that the crosshairs are in focus, repeat and find the average, avoid error of parallax.
Object, (converging) lens, screen /search pin
Sharp image (state/imply) // no parallax (between image and search pin)
Measure (distance) from image/screen to (centre of) lens
- Measure from the centre of the lens (to the screen) / measure perpendicular distance /avoid parallax error
- 1/u + 1/v = 1/f
Correct substitution
f = 15.3 cm, 15.8 cm, 15.4 cm
fave = (15.5 ± 0.4) cm
- Object would be inside the focal point so an image cannot be formed on a screen
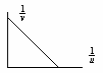Alternative (graphical method):
1/u |
0.050 |
0.033 |
0.025 |
1/v |
0.0153 |
0.0300 |
0.0398 |
Inverse values for u and for v
Plot points
Read intercept(s)
f = (15.87 ± 0.40) cm
Focus the image of a distant object on a screen.
The distance from the lens to screen corresponds to the focal length.
- Set up as shown.
Adjust the position of the screen until a sharp image is seen.
u/cm |
20.0 |
25.0 |
35.0 |
45.0 |
v/cm |
66.4 |
40.6 |
27.6 |
23.2 |
f/cm |
15.4 |
15.5 |
15.4 |
15.3 |
1/u+ 1/v = 1/f
Average = 15.4 cm
- Image not sharp / parallax error in reading distance / not measuring to centre of lens / zero error in metre stick.
Source : http://www.thephysicsteacher.ie/LC%20Physics/Student%20Notes/5.%20Lenses.doc
Web site link: http://www.thephysicsteacher.ie
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Lenses
Lenses
Lenses
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Lenses mean ? Which is the meaning of Lenses?
Lenses physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us