Moment of a force
Moment of a force
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Moment of a force
As well as causing an object to accelerate, a force may cause a body to turn or rotate, i.e. a force can have a turning effect.
To quantify this turning effect we have the following relationship, called The Moment of a Force:
Moment of a force = force × perpendicular distance
The unit of moment of a force is the Newton metre (Nm).
Two laws of Equilibrium
If an object is in equilibrium then:
- The vector sum of the forces in any direction is zero (forces up = forces down, i.e. it’s not accelerating).
- The sum of the moments about any point is zero (moments clockwise = moments anti-clockwise, i.e. it’s not rotating).
A couple
Two parallel forces with the same magnitude acting in opposite directions are called a couple.
For example turning a steering wheel (or two people on opposite ends of a revolving door).
Moment of a couple: Torque
The moment of a couple is known as Torque
Moment of a couple (Torque) = Force x Distance
Torque = force × distance
The distance in this case corresponds to the distance between the two forces – not distance between one force and middle).
Mandatory Experiment: To verify the Laws of Equilibrium for a set of coplanar Forces.
Did you know?
Text-books often suggest that a water-dam is wider at the base because the pressure is greater at greater depths, but while this is true a bigger problem is the moment of the force from the water flowing on top. Can you see why?
Leaving Cert Physics Syllabus
Content |
Depth of Treatment |
Activities |
STS |
|
|
|
|
Moments |
Definition. |
Simple experiments with a number of weights. |
Torque, e.g. taps, doors. |
|
|
|
|
Conditions for equilibrium |
Vector sum of the forces in any direction is zero. The sum of the moments about any point is zero. |
Appropriate calculations. |
Static and dynamic equilibrium. |
INVESTIGATION OF THE LAWS OF EQUILIBRIUM FOR A SET OF CO-PLANAR FORCES
APPARATUS: Two newton-meters, metre-stick, weights, paperclips, spirit-level, electronic balance
DIAGRAM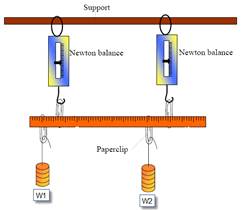
PROCEDURE
- Find and note the centre of gravity of the metre-stick by hanging it from a thread and adjusting the position of the thread such that the metre-stick is horizontal.
- Find and note the mass of the metre-stick by weighing it on an electronic-balance.
- Set up the apparatus as shown and move the weights around until the stick is horizontal and in equilibrium (not rotating). The newton-metres must be vertical.
- Record the reading on each newton-metre and the positions on the metre stick of each weight, each newton-metre and the values of the weights themselves.
RESULTS AND CALCULATIONS
FIRST LAW: TOTAL FORCES UP = TOTAL FORCES DOWN
RUN No. |
1st |
2nd |
Total Upward Forces (N) |
W1 |
W2 |
Weight of metre stick |
Total Downward Forces (N) |
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
SECOND LAW: TOTAL MOMENTS CLOCKWISE = TOTAL MOMENTS ANTI-CLOCKWISE
Clockwise Moments
Run No. |
W1 |
d1 |
W1d1 |
W2 |
d2 |
W2d2 |
Wms |
dms |
Wdms |
Total |
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Run No. |
f3 |
d3 (m) |
f3d3 (N m) |
f4 |
d4 (m) |
f4d4 (N m) |
Total moments anti-Clockwise |
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Anti-Clockwise Moments
CONCLUSION
We can see from our results that we were able to verify both laws within the margins of experimental error.
SOURCES OF ERROR / PRECAUTIONS
- Ensure that the Newton balances are vertical and the metre stick is horizontal when readings are taken.
- Use large weights (i.e. multiples of 1N) to reduce percentage errors.
NOTES
Why do we have to ensure that all forces are vertical?
Because the moment of a force is defined as being equal to the force multiplied by the perpendicular distance between the force and the fulcrum. So the easiest way of making sure that forces and distances are perpendicular to each other is to have the metre-stick horizontal and then all other forces must be perpendicular to this, i.e. vertical.
Do we have to use the extreme left hand side as our reference point?
When calculating the moments, we generally use the 0 cm mark as our fulcrum, and measure all distances from this point. Strictly speaking we could take any point on the metre stick as our reference point (or fulcrum) but the 0 cm mark is the easiest.
You should be able to work out the calculations about other points (in the 2002 exam students were asked to calculate the moments about the 10 cm mark). Apart from all distances now being calculated from the 10 cm mark, the other change could be that some forces which exerted a clockwise moment about the 0 cm mark may now exert an anti-clockwise moment about the 10 cm mark.
Some of the first questions in the text-book ask you to calculate moments about various positions on the same metre-stick; it’s good practice and re-enforces the concept that the actual position of the fulcrum doesn’t matter in these situations.
Watch out!
Setting up the apparatus can be time-consuming and the whole set-up can be rather precarious, so you might want to consider the following advice:
As soon as you have everything set-up and balanced, sketch a diagram of it and indicate on it the position and force of each object.
This should be done as quickly as possible while the apparatus is still stable before some nutter bangs against it and brings it all crashing down.
Then the tears will start.
Once you have all the relevant readings you should fill in the table and work out the calculations – that way if your results are way off you can double-check them without setting everything up again.
You have been warned!
Use large weights
Not only will the large weights reduce the percentage errors associated with the weights themselves, but they will also help to mask errors associated with the various forces not being horizontal and vertical.
If you are feeling adventurous you could try three or four weights acting down, rather than just two.
Exam Questions
- [2003 OL][2006 OL]
Define the moment of a force.
- [2006]
Why is it easier to turn a nut using a longer spanner than a shorter one?
- [2003 OL]
Explain why the handle on a door is on the opposite side to the hinges of the door.
- [2006 OL]
A crane is an example of a lever. Give another example of a lever.
- [2010]
What are the two conditions for the equilibrium of a set of co-planar forces?
- [2003]
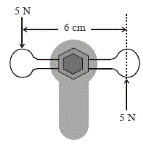
The diagram shows forces of 5 N applied to a water tap.
Calculate the moment of the couple (torque) on the tap.
- [2003 OL]
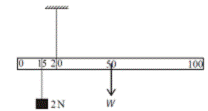
- A metre stick is suspended by a thread at the 20 cm mark as shown in the diagram. The weight W of the metre stick acts through the 50 cm mark. A weight of 2 N is placed at the 15 cm mark.
Calculate the moment of the 2 N weight about the 20 cm mark.
- What is the moment of W about the 20 cm mark?
 If the metre stick is in equilibrium, find the value of W.
If the metre stick is in equilibrium, find the value of W.
- [2009 OL]
A man opens a door by applying a force of 5 N to the door.
The distance from the point of application of the force to the fulcrum is 120 cm.
Calculate the moment of the applied force. (M = Fd)
- [2006 OL]
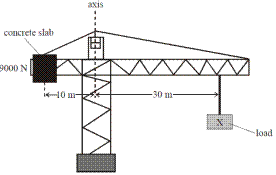
- The diagram shows a crane in equilibrium.
Give one condition that is necessary for the crane to be in equilibrium.
- What is the moment of the 9000 N concrete slab about the axis of the crane?
- Calculate the value of the load marked X.
Mandatory Experiment
- [2007 OL]
 A student investigated the laws of equilibrium for a set of co-planar forces acting on a metre stick. The weight of the metre stick was 1.2 N and its centre of gravity was at the 50 cm mark.
A student investigated the laws of equilibrium for a set of co-planar forces acting on a metre stick. The weight of the metre stick was 1.2 N and its centre of gravity was at the 50 cm mark.
The student applied the forces shown to the metre stick until it was in equilibrium.
- How did the student know the metre stick was in equilibrium?
- Copy the diagram and show all the forces acting on the metre stick.
- Find the total upward force acting on the metre stick.
- Find the total downward force acting on the metre stick.
- Explain how these values verify one of the laws of equilibrium.
- Find the sum of the anticlockwise moments of the upward forces about the 0 mark.
- Find the sum of the clockwise moments of the downward forces about the 0 mark.
- Explain how these values verify the other law of equilibrium.
- [2007]
A student investigated the laws of equilibrium for a set of co-planar forces acting on a metre stick.
The student found that the centre of gravity of the metre stick was at the 50.4 cm mark and its weight was 1.2 N.
- How did the student find the centre of gravity?
- How did the student find the weight, of the metre stick?
- Why is the centre of gravity of the metre stick not at the 50.0 cm mark?
- The student applied vertical forces to the metre stick and adjusted them until the metre stick was in equilibrium.
How did the student know that the metre stick was in equilibrium?
The student recorded the following data.
position on metre stick/cm |
11.5 |
26.2 |
38.3 |
70.4 |
80.2 |
magnitude of force/N |
2.0 |
4.5 |
3.0 |
5.7 |
4.0 |
direction of force |
down |
up |
down |
up |
down |
- Calculate the net force acting on the metre stick.
- Calculate the total clockwise moment about a vertical axis of the metre stick.
- Calculate the total anti-clockwise moment about a vertical axis of the metre stick.
- Use these results to verify the laws of equilibrium
- [2002]
A student investigated the laws of equilibrium for a set of co-planar forces acting on a metre stick.
The weight of the metre stick was 1 N and its centre of gravity was found to be at the 50.5 cm mark.
Two spring balances and a number of weights were attached to the metre stick.
Their positions were adjusted until the metre stick was in horizontal equilibrium, as indicated in the diagram.
The reading on the spring balance attached at the 20 cm mark was 2 N and the reading on the other spring balance was 4 N.
The other end of each spring balance was attached to a fixed support.

- Calculate the sum of the upward forces and the sum of the downward forces acting on the metre stick.
- Explain how these experimental values verify one of the laws of equilibrium for a set of co-planar forces.
- Calculate the sum of the clockise moments and the sum of the anticlockwise moments about an axis through the 10 cm mark on the metre stick.
- Explain how these experimental values verify the second law of equilibrium for a set of co-planar forces.
- Describe how the centre of gravity of the metre stick was found.
- Why was it important to have the spring balances hanging vertically?
Exam Solutions
- The moment of a force = the force × perpendicular distance between the force and the fulcrum.
- The distance from the fulcrum is greater therefore there is a greater turning effect.
- In order to maximise the distance between the force and the fulcrum.
- Crowbar / nailbar / nutcracker / wheelbarrow / tongs / door handle etc.
- Forces up = forces down // (algebraic) sum of forces acting is zero
(Algebraic) sum of the moments (of the forces about any point) is zero
- Moment = force × distance = 5 × .06 = 0.3 N m
- M = F × d = 2 × 0.05 = 0.1N m
- M = F × d = 0.3 W
- 0.1 = 0.3W Þ W = 0.33 N
- Moment = 5 × 1.2 = 6 N m
- The clockwise moments must equal the anticlockwise moments.
- Moment = F × distance = 9000 × 10 = 90000 N m.
- 9000 × 10 = 30x Þ x = 3000 N.
Mandatory Experiment
- It was level / horizontal / no movement.
- As in the diagram, but there should also be the weight of the metre stick (1.2 N) shown at the 50 cm mark.
- 20.2 N
- 15 + 4 + 1.2 = 20.2 N
- The sum of forces is zero / the upward forces = the downward forces
- Moment = F × d: (0.3 × 10) + (0.9 × 10.2) = 12.18 N m
- Moment = F × d: (0.27 × 4) + (0.5 × 1.2) + (0.7 × 15) = 12.18 N m
- The sum of the moments is zero (sum of clockwise moments = sum of anti-clockwise moments)
- By hanging the metre stick on a thread support and adjusting the position of the thread until the metre stick remained horizontal.
- By putting it on an electronic balance.
- The material is not of perfectly uniform density.
- The metre stick was at rest.
- Fup = 4.5 + 5.7 = 10.2 N and Fdown = 2 + 3 +1.2 +4 = 10.2 N
Þ net force = 0
- (through zero) Moment = 2(0.115) + 3(0.383) +1.2(0.504) +4.0(0.802) = 0.23+1.149+0.6048+3.208 = 5.2 N m
- (through zero) Moment = 4.5(0.262) +5.7(0.704) = 5.1918 N m = 5.2 N
- Fup = Fdown
Total clockwise moments = Total anti-clockwise moments
- Up = 2 +4 = 6 (N)
Down = 2 +1 +1.8 + 1.2 = 6 (N)
- The vector sum of the forces in any direction is zero (forces up = forces down).
- Moment = force × distance
Sum of anticlockwise moments = 2.8 N m
Sum of clockwise moments = 2.8 N m
- The sum of the moments about any point is zero.
- Hang the metre stick on a string and adjust the position until the metre stick balances.
Note the position.
- Moment of a force = force × perpendicular distance, so if the readings on the metre stick are to correspond to these perpendicular distances then the metre stick must be perpendicular to the spring balances, and if the metre stick is horizontal then the spring balances should be vertical.
Source : http://www.thephysicsteacher.ie/LC%20Physics/Student%20Notes/10.3%20Moments.doc
Web site link: http://www.thephysicsteacher.ie
Author : not indicated on the source document of the above text
Moment of a force
Moment of a force
Moment of a force
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Moment of a force mean ? Which is the meaning of Moment of a force?
Moment of a force physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us