Potential difference and capacitance
Potential difference and capacitance
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Potential difference and capacitance
The Potential difference (p.d.) between two points is the work done in bringing a charge of 1 Coulomb from one point to the other*.
The unit of potential difference is the Volt (symbol V)
The Volt
The potential difference between two points is one volt if one Joule of work is done when bringing a charge of one Coulomb from one point to another.
A more common (but less correct) word for the term ‘potential difference’ is ‘Voltage’.
Note that potential difference is always between two points.
Relationship between Work, Charge and Voltage
W = V × Q
See Worked Problems 1 – 6, Page 236.
In particular problems 5 and 6 should be tried, but perhaps No. 5 should be left until 6th year. Then try 1 – 8, Page 237.
Potential at a Point*
The potential at a point refers to the work done in bringing a positive charge from that point to earth.
Leaving Cert Physics Syllabus: Potential Difference
Content |
Depth of Treatment |
Activities |
STS |
|
Definition of potential difference: |
Appropriate calculations. |
|
Capacitance*
The symbol for capacitance is C
Please don’t confuse ‘Capacitance’ (symbol C) with ‘Charge’ (symbol Q).
A capacitor is an electrical device used to store charge
The Capacitance of a conductor is the ratio of the charge on the conductor to its potential*.
The unit of capacitance is the Farad; symbol is F.
(This is similar to the definition for Resistance; 
which we will come across in the next chapter.)
The Parallel Plate Capacitor*
Consider two oppositely charged parallel plates as shown*
From the diagram we can see that the capacitance will increase if the common area between plates (A) increases, or if the distance between plates (d) decreases.
Therefore C µ A and C µ 
Þ C µ 
Þ C = k 
The proportional constant turns out to be e (remember we came across this in the last chapter as part of Coulomb’s Law) and represents the permittivity of the medium between the two plates.
Þ
See worked examples 11 and 12, page 241. Then try questions 1 – 5, page 243
To Demonstrate the Factors affecting the Capacitance of a Parallel Plate Capacitor*
- Connect the two parallel plates to a digital multi-meter (DMM) set to read capacitance. Note the capacitance.
- Increase the distance between them – note that the capacitance decreases.
- Move one plate slightly to the side (decreasing the overlap area) – note that the capacitance decreases.
- Place different slabs of insulating material between the plates – note that the capacitance is lowest when nothing (air) is between the plates*.
Two Formulae for the Energy stored in a Capacitor*
W = 
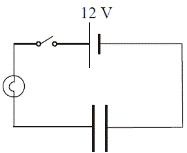
To show that a Charged Capacitor stores Energy 
- Set up as shown.
- Close the switch to charge the capacitor.
- Remove the battery and connect the terminals together to ‘short’ the circuit.
- The bulb will flash as the capacitor discharges, showing that it stores energy.
Common Uses of Capacitors
- The ‘flash’ on a camera
- Smoothing out variations in direct current
- Allows alternating current (a.c.) to pass through it but blocks direct current (d.c.)*.
- Used in circuits to only allow alternating current of a specific frequency to flow*
Leaving Cert Physics Syllabus: Capacitance
Content |
Depth of Treatment |
Activities |
STS |
|
|
|
|
Capacitors and |
Definition: C = Q/V |
|
|
|
Parallel plate capacitor. |
Demonstration that capacitance depends on the common area, the distance between the plates, and the nature of the dielectric. |
Common uses of capacitors: |
|
Energy stored in a capacitor. Use of W = ½ CV 2 Capacitors – conduct a.c. but not |
Charge capacitor–discharge through lamp or low-voltage d.c. motor. Appropriate calculations. |
|
Extra Credit
*Definition of Potential Difference
Note:
If the +1 charge is going to a positive point then work has to be done to get it there, but if it’s going to a negative point then it (the +1 charge)does the work.
This is similar to saying that a rock on top of a cliff has a potential energy of, say, 100 Joules.
To get the rock up there you have to do 100 Joules of work on the rock, or alternatively if the rock fell to the ground it would do 100 Joules of work.
*W = V Q
Now if you know how much gravitational energy the rock has (from the formula for gravitational potential energy E = mgh), you can calculate the velocity at which it will hit the ground (from the formula for kinetic energy E = ½ mv2).
From Conservation of Energy; Potential Energy = Kinetic Energy: mgh = ½ mv2
Just as the rock will accelerate towards the ground, so the positive charge will accelerate towards the negative point.
In fact, if you know how much potential energy the charge had to begin with, i.e. the potential between the two points (from the formula W = QV) you can calculate its velocity when it reaches the second point (if you know its mass) by again using
Potential Energy = Kinetic Energy, or QV = ½ mv2
*Potential at a Point
Remember above that we noted potential difference is always between two points?
Well quite often we need to know how difficult it is to bring positive charge from the earth to a positive object.
Because this occurs so often, we dispense with the term ‘potential difference’ and just refer to the potential difference between the earth and the object as ‘the potential of the object’ – this is also known as ‘the potential at a point’.
From this it should be obvious that the more positive charge an object has, the more work will have to be done in bringing another positive charge up to it, and so the potential at that point will be greater.
You might now want to challenge yourself to explain how a Gold Leaf Electroscope can be used to compare the potential difference between one object and the earth versus another object and the earth (see page 235 for a big hint).
*Capacitance
Picture a water container.
The amount of water the container can hold (its capacity) will depend on – among other things – how quickly the water level rises when water is poured in; if the water level rises rapidly it suggests the container must be quite narrow and therefore may not hold much water.
We would deduce that the container had a small ‘capacitance’.
An electrical capacitor can be compared to this water container and the rate at which the potential of the capacitor increases gives us an indication of how much charge the capacitor can hold; if putting a small charge on it raises its potential considerably, then its capacitance must be small.
Remember ‘raises its potential considerably’ means that a lot more work needs to be done to bring further charge up to it.
So for example if a capacitor has a capacitance of 2 farads, then putting a charge of 6 coulombs on it will increase its potential by 3 volts (from C = Q/V, so V = Q/C).
However if the capacitor had a capacitance of 200 farads, putting a charge of 6 coulombs on it would only raise its potential by 0.03 volts.
*Definition of Capacitance
If, when asked to define Capacitance, you answer that “it is used to store charge”, you will get zero marks, because this is not a definition.
*C = Q/V
It’s easier to remember the formula C = Q/V if you re-arrange it as Q = CV
*The Parallel Plate Capacitor
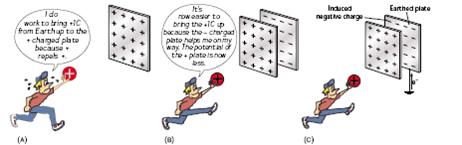
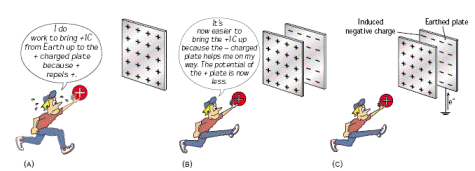
The potential of a positively charged object is an indication of how much work will have to be done to bring another positively charged object up to it.
Therefore the more positive charge that is on the object, the greater its potential will be.
If however we bring a negatively charged object up close to the positively charged object, their electricity fields will tend to cancel each other out, and it will then become easier to bring more positive charge up to the original – positively charged – object.
This means that the potential of the original object becomes reduced simply by bringing an oppositely charged conductor up close to it.
This is the principle upon which a parallel plate capacitor is based.
*Consider two oppositely charged parallel plates as shown
The key to this is to remember that the more their electric fields cancel each other out, the greater will be the capacitance of the system.
*Two Formulae for the Energy stored in a Capacitor
W = ½ CV2, W = Q2/2C
You don’t need to know how to derive these formulae, but it is actually very straightforward and, for me at least, it’s easier to derive them from scratch than to remember them.
They derivation incorporates the formulae W = QV, and C = Q/V.
I can show you on the board in 5 minutes if you ask me.
Note that if you start with Q = CV, and substitute this into W = QV, you get W = CV, with no factor of ½!
To explain where the factor of ½ comes from requires going over the derivation, so go on – ask me!
By the way, the text-books don’t explain this apparent anomaly.
*Allows alternating current (a.c.) to pass through it but blocks direct current (d.c.)*.
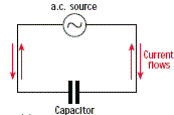
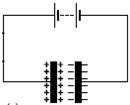
In the first diagram (direct current) once the circuit is complete there is a sudden movement of electrons, but because the circuit is not complete there is no further flow.
In the second diagram the plates are continuously charging and discharging; the time this takes (and therefore the frequency) depends upon the size of the plates (see next point).
Strictly speaking the current is not ‘passing through’ the capacitor, but merely acts as though it is.
*Used in circuits to only allow alternating current of a specific frequency to flow
This in turn is used in radios to only receive certain frequencies, corresponding to radio waves coming from a specific radio station.
The part of an electronic circuit responsible for this is called an ‘RC’ circuit (for Resistance, Capacitance).
When changing stations in a radio, you are really changing the capacitance of this part of the circuit.
How does this work?
Well the larger the size of the capacitor, the longer it takes to discharge (and charge). Now if the time it takes to charge and discharge corresponds to the frequency of the alternating current – which in turn is carrying the sound information from the radio station – then this signal will be allowed to pass and ultimately to reach the speakers.
*To Demonstrate the Factors affecting the Capacitance of a Parallel Plate Capacitor
Note: An alternative demonstration is given on page 242, but it is ridiculously difficult to understand what’s going on – the textbook does not explain it fully.
The demonstration described is perfectly adequate and is very easy.
*Place different slabs of insulating material between the plates – Note that the capacitance is lowest when nothing (or air) is between the plates.
This may seem confusing, so if it’s bothering you, ask me to explain why.
Exam questions
- [2005][2004][2009][2002 OL]
Define potential difference.
- [2007 OL]
Name an instrument used to measure potential difference.
- [2009][2008][2004] [2002 OL]
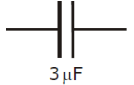Define capacitance.
- [2004 OL]
Name the electrical component represented in the diagram.
- [2006 OL][2006 OL][2007 OL][2010]
Give one use of a capacitor.
- [2010]
Which of the following devices is adjusted when tuning into a radio station?
Transformer, diode, capacitor, rheostat
- [2006]
List the factors that affect the capacitance of a parallel plate capacitor.
- [2008]
How would you demonstrate that the capacitance of a parallel plate capacitor depends on the distance between its plates?
- [2010]
What is the positive charge stored on a 5 μF capacitor when connected to 120 V d.c. supply?
- [2006]
- The plates of an air filled parallel plate capacitor have a common area of 40 cm2 and are 1 cm apart. The capacitor is connected to a 12 V d.c. supply. Calculate the capacitance of the capacitor.
(Permittivity of free space = 8.85 × 10-12 F m-1)
- Calculate the magnitude of the charge on each plate.
- What is the net charge on the capacitor?
- [2004][2009][2002 OL]
Describe an experiment to demonstrate that a capacitor can store energy.
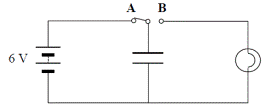
- A capacitor is connected to a switch, a battery and a bulb as shown in the diagram. When the switch is moved from position A to position B, the bulb lights briefly.
- What happens to the capacitor when the switch is in position A?
- Why does the bulb light when the switch is in position B?
- When the switch is in position A the capacitor has a charge of 0.6 C, calculate its capacitance.
- [2007]
Calculate the energy stored in a 5 μF capacitor when a potential difference of 20 V is applied to it.
- [2005]
A capacitor of capacitance 100 μF is charged to a potential difference of 20 V. What is the energy stored in the capacitor?
- [2002]
How much energy is stored in a 100 μF capacitor when it is charged to a potential difference of 12 V?
- [2009]
The ability of a capacitor to store energy is the basis of a defibrillator. During a heart attack the chambers of the heart fail to pump blood because their muscle fibres contract and relax randomly. To save the victim, the heart muscle must be shocked to re-establish its normal rhythm.
A defibrillator is used to shock the heart muscle.
A 64 μF capacitor in a defibrillator is charged to a potential difference of 2500 V.
The capacitor is discharged in 10 milliseconds through electrodes attached to the chest of a heart attack victim.
- Calculate the charge stored on each plate of the capacitor.
- Calculate the energy stored in the capacitor.
- Calculate the average power generated as the capacitor discharges.
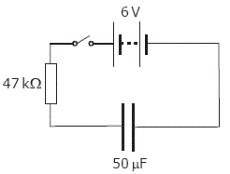[2004]- The circuit diagram shows a 50 μF capacitor connected in series with a resistor, a 6 V battery and a switch.
The potential difference across the capacitor is 2.24 V initially when the current is 80 μA.
Calculate the charge on the capacitor at this instant.
- Calculate the energy stored in the capacitor when it is fully charged.
- Describe what happens in the circuit when the 6 V d.c. supply is replaced with a 6 V a.c. supply.
- [2002 OL]
Diagram A shows a capacitor connected to a bulb and a 12 V a.c. supply.
Diagram B shows the same capacitor connected to the bulb, but connected to a 12 V d.c. supply.
What happens in each case when the switch is closed? Explain your answer.
Exam Solutions
- The potential difference between two points is the work done in bringing a charge of 1 Coulomb from one point to the other.
- A voltmeter
- The capacitance of a conductor is the ratio of the charge on the conductor to its potential.
- A capacitor
- Store charge / (radio) tuning / smoothing / store energy / flash guns for cameras, phone charger, blocks d.c.
- Capacitor
- Common area of plates, distance apart, permittivity of dielectric between plates.
- Connect the two parallel plates to a digital multi-meter (DMM) set to read capacitance.
Note the capacitance.
Increase the distance between them – note that the capacitance decreases.
- Q = CV = (5 × 10–6)(120)
Q = 6.0 × 10–4 C
- C=εA/d
C = [(8.85 × 10-12)(40 × 10-4)] / (0.01)
C = 3.54 × 10-12 F
- Q = C V
Q = (3.54 x 10-12)(12) = 4.2(5) x 10-11 C
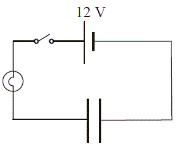Zero- Set up as shown.
- Close the switch to charge the capacitor.
- Remove the battery and connect the terminals together to ‘short’ the circuit.
- The bulb will flash as the capacitor discharges, showing that it stores energy.
- It charges (charge builds up on the plates).
- The capacitor discharges so current briefly runs through the bulb.
- C = Q/V = 0.6/6 = 0.1 Farads
- E = ½ CV2 = ½ (5 x 10-6)(20)2 = 1.0 x 10-3 J
- E = ½CV2 Þ E = ½(100 × 10-6)(20)2 = 0.02 J
- E = ½ CV2 = ½ (100 × 10-6)(12)2 = 7.2 × 10-3 J
- C = Q/v Þ q = CV Þ q = (64 × 10-6)(2500) Þ q = 0.16 C
- E = ½ CV2 = ½ (64 × 10-6)(2500)2 = 200 J
- P = W/t = (200)/(10 × 10-3) = 20000 W
- C = Q/V Þ Q = CV = (50 ×10−6)(2.24) = 1.12 × 10-4 C
- E = ½ CV2 = ½ (50 ×10− 6)(6 )2 = 9 ×10−4 J
Note that here we use 6 Volts as the potential difference across the capacitor because although the potential difference at the beginning is 2.24 V, when the capacitor is fully charged it takes the maximum amount of energy to put more charge on.
- The current will flow continually.
- In diagram A the bulb lights because a capacitor ‘conducts’ a.c. (it is continually charging and discharging).
In diagram B the bulb does not light because a capacitor does not conduct d.c.
Source : http://www.thephysicsteacher.ie/LC%20Physics/Student%20Notes/20.%20Potential%20Difference%20and%20Capacitance.doc
Web site link: http://www.thephysicsteacher.ie
Author : not indicated on the source document of the above text
Potential difference and capacitance
Potential difference and capacitance
Potential difference and capacitance
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Potential difference and capacitance mean ? Which is the meaning of Potential difference and capacitance?
Potential difference and capacitance physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us