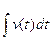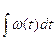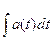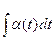Rotation and statics
Rotation and statics
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Rotation and statics
Rotation and Statics Notes
The first thing you need to know about rotation is that you can use everything you’ve learned up to this point with different symbols. You have all the physics knowledge already, you just need to make the analogy between transitional motion and rotation. These notes assume the rotation of a rigid body.
Rotational Kinematics
Rotational Kinematics is very similar to the kinematics we’ve already done. The first new idea is that instead of using a distance that you can measure in meters, we will think of our distance as an angle traveled in radians. We’ll call this theta, symbolized by q. This angle is measured counterclockwise.
This means that angular velocityis the angle covered per unit time. Angular velocity is a vector, and it follows the right hand rule. Curl your right hand in the direction of motion and your thumb points in the direction of the angular velocity.
w=
average or constant angular velocity. Units: rad/s
likewise, angular acceleration is the change in angular velocity per unit time. It’s vector points in the same direction as the torque vector (later in these notes)
a=
average or constant angular acceleration. Units: rad/s2
We can also relate the angular concepts to the tangential concepts of distance, velocity and acceleration at some point by considering the distance from the axis of rotation (center of the circle) to that point, r. In the case when we want to solve for those concepts on the outside of the circle, r is the radius of the circle.
d= rq v= rw a= ra
Just so you don’t get tricked, the total linear acceleration is both the tangential acceleration and the centripetal acceleration.
We can now incorporate our knowledge of transitional motion to this new concept of rotation with some constant acceleration equations.
Linear |
Rotational (angular) |
Vave= |
wave= |
aave= |
aave= |
xf = x0 + vot + ½at2 |
qf = q0 + wot + ½at2 |
vf = vo + at |
wf= wo + at |
vf2 = v02 + 2aDx |
wf2 = w02 + 2aDq |
d= rq v= rw a= ra |
|
Of course, if you aren’t given a constant acceleration (meaning that there is a time term in the accelration equation) you have to use calculus!
In that case:
Linear |
Rotational (angular) |
v(t) = |
w(t)= |
a(t)= |
a(t)= |
x(t) = |
q(t) = |
v(t) = |
w(t) = |
= x’(t) 
= q’(t)
= v’(t)
= w’(t)
Remember that when you integrate, you must add a constant + c to determine the initial conditions like the initial (angular) velocity or the initial (angular) distance.
Rotational Inertia
Rotational Inertia is the rotational analogue of mass. Just like mass determines how easy it is to accelerate an object, rotational inertia determines how easily an object can rotate. We find that with more mass, the rotational inertia increases. The distribution of mass is also a determining factor. For bodies of equal mass, the object that has mass distributed farther from the axis of rotation will have the greater rotational inertia.
The amount of rotational inertia, also known as the moment of inertia, I, can be calculated in a few different ways.
It is often given to you as an equation, such Ihoop=MR2 where M is the mass of the hoop and R is the radius of the hoop and you just need to plug in the correct values.
Other times, however, you will need to find the equation.
For a body with discrete particles of mass, we can find I by summing up each individual I with
I = S miri2
For a continuous body, however, the sum becomes an integral.
I = 
r2dm
The limits of integration will depend on the shape that you choose.
The hardest part about solving these problems is getting r and m to be in terms of the same variable. In order to do this you need to first set up an equation for density as total mass/total amount of space (length, area or volume depending on how many dimensions your object is). Then equate that to dm/dx(or dA or dV) and find the relationship between r and m so that you have one variable and the rest constants. You can then plug it in to the equation and integrate!
You can also use the parallel-axis theorem to find I for an object at some arbitrary axis if you know it’s I when axis is along the center of mass.
I’ = Icm + Mx2
where I’ is the I about some arbitrary axis,
Icm is the I when the center of mass is taken as the axis
M is the mass of the entire system
X is the distance from the center of mass(old axis) to the new axis
This is called the parallel axis theorem because the new axis must be parallel to Icm
Center of Mass
We’ve previously dealt with CM, but now that you can find rotational inertias, you can use calculus to find the center of mass of a continuous object.
M rcm = 
r dm
Rotational Dynamics
Torque is the rotational analogue to force. Force is a push or pull that causes an acceleration. Torque is a twist that causes a rotational acceleration.
t = r x F = r F sinq
where F is the force exerted, r is the distance from the force to the axis of rotation and q is the angle between them. Basically, the cross product here insures that you are using the component of force that is perpendicular to r.
To determine the direction of torque, which is vector, we use the right hand rule that we would use for any cross products. Any torque that causes a counterclockwise turn is positive (it will be in the positive z-axis) and a torque that causes a clockwise turn is negative (it will be in the negative z-axis). This makes sense because we measure +q as a counterclockwise angle.
We can add and subtract torques just like we have done with forces and use an analogous equation to Newton’s 2nd law.
Linear |
Rotational (angular) |
S F = ma |
S t = Ia |
t = r x F |
|
It will often be necessary to use the torque equations along with forces and FBDs, such as when you need to solve pulley problems where the pulley has a mass.
Energy, Work, Power
Rotational Kinetic Energy is the energy due to the rotation of an object.
All of the equations that we have previously studied, like conservation of energy and power still hold true.
Uo + Ko + Wother = Uf + Kf
P= 
Linear |
Rotational (angular) |
K = ½ mv2 |
K = ½ Iw2 |
W = |
W = |
P = F |
P = t |
F dx
t dq
v
wA rolling object has both translational and rotational kinetic energy, so
K = ½ mv2 + ½ Iw2
Angular Momentum
Angular Momentum is the rotational analogue to linear momentum. Like torque, there are two ways to solve for it.
L = r x p = r p sin q
where p is the linear momentum, r is the distance from the force to the axis of rotation and q is the angle between them. This is another cross product that follows the right hand rule.
We can also use analogous equations to our linear momentum equations:
Linear |
Rotational (angular) |
p = mv |
L = Iw |
F = |
t = |
K = |
K = |
L = r x p |
|
We know that linear momentum is conserved when there is no net external force acting on the system. Likewise, angular momentum is conserved when there is no net external torque acting on the system. The conservation of angular momentum is particularly useful when there are collisions involved with rotating objects.
L0 = Lf
I0w0 = Ifwf
or in cases with more than one object in a system,
I10w10 + I20w20 = I1fw1f + I2fw2f
if those objects stick together:
I10w10 + I20w20 = (I1f + I2f)wf
Statics
Translational equilibrium occurs when the net force acting on an object is zero. Rotational equilibrium occurs when the net torque acting on an object is zero. Equilibrium occurs when an object is in both Translational and rotational equilibrium. This doesn’t mean that the object is not moving; it only means that it has no linear or angular acceleration.
Static Equilibrium occurs when an object is at rest and in equilibrium. That means it’s at rest and there is no net external force or torque acting on the object.
Source : http://www.groovytoo.com/robinson/AP/rotation,%20CM,%20statics%20notes.doc
Web site link: http://www.groovytoo.com/robinson/
Author : Ms. Robinson
Rotation and statics
Rotation and statics
Rotation and statics
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does rotation and statics mean ? Which is the meaning of rrotation and statics?
Rotation and statics
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us