• 

 

Simple harmonic motion and Hooke’s law

 

 

---

 

Simple harmonic motion and Hooke’s law

 

The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.

We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge

Physics

 

Simple harmonic motion and Hooke’s law

 

Hooke’s  Law

Hooke’s Law states that when an object is stretched the restoring force is directly proportional to the displacement, provided the elastic limit is not exceeded.

 

 

The most common example of Hooke’s Law is a stretched string.
See Maths Problem 1, page 147 and Exercise 13.1, Numbers 1 and 2.

 

Simple Harmonic Motion (S.H.M.)*
An object is said to be moving with Simple Harmonic Motion if;

 

 

“But I thought ω represented angular velocity?”*

 

Other examples of SHM, apart from a stretched string are:

To show that any object that obeys Hooke’s Law will also execute SHM
The aim here is to show that Hooke’s Law is a subset of S.H.M., i.e. that F µ -s can be rewritten in the form a = - w2 s.

So we start with the equation for Hooke’s Law;                    F µ -s              Þ                    F = -k s
But F =  ma                                                    Þ                 ma = -k s           

Now divide both sides by m                                                              Þ                  a = -  s                     
This is equivalent to the equation for S.H.M. where the constant w2 in this case is k/m.

 

Relationship between Periodic Time (T) and w for an object undergoing SHM*
As with waves, the periodic time is the time taken for one complete oscillation.

 

 

The Simple Pendulum
A simple pendulum consists of a light string with a mass at the end.
For an angle of swing less than approximately 50, the motion of a Simple Pendulum can be considered to be SHM.

 

Periodic Time of a Simple Pendulum

  

 

Mandatory Experiment:
Investigation of the relationship between period and length for a simple pendulum, and hence calculation of g.

Leaving Cert Physics Syllabus

 

INVESTIGATION OF THE RELATIONSHIP BETWEEN PERIODIC TIME AND LENGTH FOR A SIMPLE 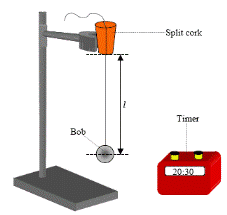PENDULUM AND HENCE CALCULATION OF g

APPARATUS
Pendulum bob, split cork, ruler, string and timer

DIAGRAM

 

 

 

 

 

 

 

 

PROCEDURE

 

 

 

RESULTS

 

CONCLUSION
We got a value for acceleration due to gravity of 9.7 m s-2, which compares favourably with the theoretical value of 9.8
m s-2. We therefore conclude that the theory may well be correct.

 

SOURCES OF ERROR / PRECAUTIONS

Extra Credit
*F µ -s
Why the minus sign? Well because displacement is a vector, it has a direction associated with it, and this direction is always opposite to the direction of the restoring force, even though as one quantity gets bigger so does the other.

 

*Simple Harmonic Motion (S.H.M.)

Basically what’s going on is that an object has its natural resting point, and if, when it gets disturbed from this point it tries to return but actually overshoots the mark and has to return again and again, then the object is executing SHM.

 

In our study of Newton’s Laws of Motion we consider the motion of a body when subject to a constant force or forces. As a result we can calculate the object’s velocity or position at any time.

However there are many instances when a moving object is subject to a changing force – can we still calculate future position and velocity? Well, we can if we can quantify the force, i.e. if we know how the force is changing. One example of an object experiencing a changing force is a stretched spring. We say that the spring is undergoing Simple Harmonic Motion (SHM).

What happens acceleration in Simple Harmonic Motion?
Recap

Let’s take another look at this.
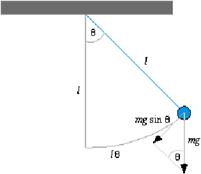
Consider a Simple Pendulum*                                                                                   

The aspect which most people find confusing here is that at the extremities the velocity is zero, while the acceleration is a maximum, whereas at the equilibrium position the opposite is the case.  How can this be? 
Answer:
You must think in terms of forces
Personally, I can’t fathom why textbooks don’t explain this by referring to forces; after all, the only way you can have acceleration is if you have a force causing it.
Acceleration is directly proportional to the force causing it, so if force is a maximum acceleration must be also, and vice versa. Now let’s look at the diagram in terms of forces.
At the equilibrium point the restoring force on the mass is zero  – it’s not being pulled to the left or the right, therefore the acceleration must be zero, whereas at the extremities the force pulling the mass back in is a maximum, therefore the corresponding acceleration must also be also be a maximum.

The other point which might cause confusion is velocity being zero at the extreme positions, but remember we came across this before; when an object is thrown up its instantaneous velocity is zero at the very top, (even though its acceleration is not zero).

* “But I thought ω represented angular velocity?”
Well spotted. ω is the same symbol as was used in the last chapter (Circular Motion) to represent angular velocity, however  it does not represent angular velocity here. It’s not just coincidence that ω turns up in both chapters; they are connected, but the relationship is a little complicated.

In the last chapter we made use of the formula v = distance/time and applied it to a satellite undergoing a full cycle where v = 2πr /T . We also had v = rω, so we can re-write the previous equation as rω = 2π r/T. Cancel r’s to get ω = 2π /T.
Cross-multiply to get T = 2π/ω.
Hmmm . . . - what does a stretched string have to do with circular motion?

Exam Questions

State Hooke’s law.

A mass at the end of a spring is an example of a system that obeys Hooke’s Law.
Give two other examples of systems that obey this law.

Name this law and give a statement of it.

Describe the motion of the sphere when it is released.

Calculate its spring constant.

The sphere is then released and oscillates about a fixed point.
Derive the relationship between the acceleration of the sphere and its displacement from the fixed point.

When the cyclist rides the bike over a bump on a track, the frame of the bike and the cyclist oscillate up and down.
Using the formula F = – ks, calculate the value of k, the constant for the springs of the bike.

Calculate the period of oscillation of the cyclist.

 

Section A questions

A student investigated the relationship between the period and the length of a simple pendulum. The student measured the length l of the pendulum.
The pendulum was then allowed to swing through a small angle and the time t for 30 oscillations was measured.
This procedure was repeated for different values of the length of the pendulum.
The student recorded the following data:

 

 

In investigating the relationship between the period and the length of a simple pendulum, a pendulum was set up so that it could swing freely about a fixed point.
The length l of the pendulum and the time t taken for 25 oscillations were recorded.
This procedure was repeated for different values of the length.
The table shows the recorded data.

The pendulum used consisted of a small heavy bob attached to a length of inextensible string.

 

Exam Solutions

A stretched spring obeys Hooke’s law.

 

Because the spring is in equiblibrium this must be equal to the force up (which is the restoring force).
Hooke’s law in symbols: F = k x
Þ (0.5)(g) = kx     Þ k = F/x = 0.5g/0.030                      Þ k = 163.3 N m-1

Þ a = kx/m = (163.3)(0.02)/(0.5) = 6.532 m s-2
OR
a = w2 x Þ            w2 = k/m = 163.3/0.5 Þ a = 6.532 m s-2

mg  = ks
(0.30)(9.8) = (k)(0.085)
k = 34.6 N m-1

• F = - ks      Þ        ma = - ks         Þ        a = - (k/m)s      Þ        a α -s Þ        a = - k s
• Its acceleration is proportional to its displacement from a fixed point.
• From above: ω2 = k/m  Þ  ω2 = 34.6 / 0.3           Þω = 10.7 ÞT = 2π/ω  = 2π/10.7 = 0.58 ≈ 0.6          Þ T = 0.6 s
• This occurs when s is a maximum, i.e. when s = amplitude = 0.310 – 0.285 = 0.025 m.

a = -ω2s     Þ        a = - (10.7)2 (0.025)    Þ        a = (-) 2.89 m s-2

• This occurs at the fixed point when l = 0.285 m

•  
• F = – ks     Þ  mg = – ks   Þ 60 × 9.8 = -k (.005)            Þ  588 = -k (.005)      Þ k  = 1.2 × 105  N m-1
• k/m = ω2

ω  = 38 s-1
T = 2π/ω = 0.16 s

• f = 1/T  ≈ 6       

 

Solutions to Section A questions

•  
• To reduce percentage error in measuring the periodic time.
• Use an inextensible string, string suspended at fixed point (e.g. split cork or two coins)

 

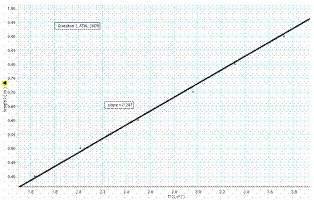• See graph

 

 

 

 

 

 

 

 

 

l /cm	40.0	50.0	60.0	70.0	80.0	90.0	100.0
t /s	38.4	42.6	47.4	51.6	54.6	57.9	60.0
Time for 1 swing/ s
t2/ s2
l /m	0.4	0.5	0.6	0.7	0.8	0.9	1.0

 

• t2 is proportional to l
• Slope = 0.25 (ms–2) [range: 0.24 – 0.25 m s–2]

g = 9.72 m s–2 [range: 9.4 – 9.9 m s–2]

 

 

•  
• To reduce air resistance and to keep the string taut
• So that length remains constant because length would be another variable.
• The string was placed between two coins (or a split cork).
• Make sure that there are no draughts / make sure it oscillates in one plane only.
• Draw a suitable graph

time for 25 swings /s	31.3	35.4	39.1	43.0	45.5	48.2
time for 1 swing/s	1.25	1.42	1.56	1.72	1.82	1.93
t2/s2	1.57	2.01	2.45	2.96	3.31	3.72
l/m	.40	.50	.60	.70	.80	.90

 

 

 

Values of t divided by 25 to get T
Axes correctly labelled  T2 vs. l
At least six points plotted correctly
Straight line drawn
Good distribution (about straight line)

• T2 is proportional to l
• The graph resulted in a straight line through the origin          

 

Source : http://www.thephysicsteacher.ie/LC%20Physics/Student%20Notes/13.%20Hookes%20Law%20and%20SHM.doc

Web site link: http://www.thephysicsteacher.ie

Author : not indicated on the source document of the above text

If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.

 

Simple harmonic motion and Hooke’s law

 

 

Simple harmonic motion and Hooke’s law

 

Main page

 

Alimentation - nutrition	Animals	Architecture	Art
Astrology, esoteric, parapsychology and fantasy	Astronomy	Biology and genetics	Botany and agriculture
Chemistry	Courses, training, guides, handbooks and tips	Culture General and actuality	Dermatology, health and wellness
Dictionaries and glossaries	Economics and finance	Education and pediatrics	Engineering and technology
English grammar and anthology	Fashion and show business	Fitness	Food, recipes and drink
Games, play space	Geography, geology and environment	History	Informatics and computer world
Jobs world	Languages	Leisure and DIY do it yourself	Lessons for students
Literature, biographies and journalism	Mathematics, geometry and statistical	Medicine	Music
Notes and concept maps	Philosophy	Photography and images - pictures	Physics
Physiology	Psychology and psychoanalysis	Quiz questions and answers	Religions
Rights law and political science	Science	Sociology and cultural anthropology	Sport
Summaries and reviews	Television, film - movies and comics	Theater and communications	Theses, themes and dissertations
Travel and tourist guides	Useful documents and tables	Utility, calculators and converters	Weather and meteorology

 

 

This is the right place where find the answers to your questions like :

Who ? What ? When ? Where ? Why ? Which ? How ? What does Simple harmonic motion and Hooke’s law mean ? Which is the meaning of Simple harmonic motion and Hooke’s law?

 

---

 

---

 

 

 

Alanpedia.com from 1998 year by year new sites and innovations

Main page - Disclaimer - Contact us