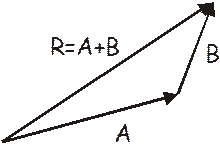Vectors
Vectors
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Vectors
Buffy peered into the dark recess of the catacombs. The feeble flame from the sputtering torch barely pierced the gloom. It had been three long months since she had first received word that the Count had somehow escaped and established himself elsewhere. She was sure that she had finally found the Count’s new hiding place. Suddenly the torch went out. There was no light – she was in total blackness. She looked around, her breathing rate increased and she began to say to herself, “Don’t panic.” Then, slowly, out of the darkness, she saw a pair of small glowing eyes. Then she heard a loud screech and suddenly there were hundreds, perhaps thousands, of the bright, luminous orbs staring at her in the blackness of that terrible place. The eyes produced light, not a lot of light, just a little. Just enough to dimly outline the bones and skulls of the dead, long lying in the depths of this, their final resting place. She shuddered. What could the creatures who eyes were so terrifying be? Rats? Yes, Buffy decided, they had to be rats, and rats can be ignored, can’t they?
It was hard being a Vampire Slayer and she wondered yet again why she was chosen. Why couldn’t she be a regular teenage girl who only had to worry about getting good grades, boyfriends, and hairstyles?
Suddenly, out of the gloom she heard the voice of the Count.
“Buffy, I am so touched that you have come such a great dist
Good heavens! The Physics Kahuna is totally confused. What has happened to the fine AP Physics handout that he has been writing? Where did this ridiculous Buffy thing come from? What is going on?
Okay, what’s done is done. We can go on, we can deal with this, we can handle it, we can get over it.
So let us get onto the subject of vectors.
Good Stuff on Vectors: We’ve briefly mentioned vectors and scalars. The time has now come to undertake a thorough study of the things.
Of the two, scalars are the easiest to understand and deal with. See, when you deal with scalars, it’s all very simple, they’re just like everyday numbers -- just use the regular arithmetic stuff that you have laboriously mastered during the past 10 – 12 years. Like adding apples with apples.
Dealing with vectors is a whole ‘nuther thang’. It’s more like adding apples and pork bellies together or something.
When you add scalars you simply do this: 2 kg + 3 kg = 5 kg.
But with vectors, 2 + 3 might equal 4! Lord, how can this be!
Well, your basic vectors have both magnitude and direction. If you add two velocities, one that is north at 10 m/s and the other is south at 10 m/s, you end up with zero m/s. Can you see why this is so?
The classic way to add vectors is to represent them with arrows, draw them to scale, and then measure out things with a ruler and protractor to see what the answer would be.
 A vector is represented as an arrow. The arrowhead points in the vector’s direction and the length represents the vector’s magnitude. To represent the magnitude, you have to use a scale to figure out how long to draw the thing. Each vector has a head and a tail.
A vector is represented as an arrow. The arrowhead points in the vector’s direction and the length represents the vector’s magnitude. To represent the magnitude, you have to use a scale to figure out how long to draw the thing. Each vector has a head and a tail.
The graphical vector addition method is sometimes called the “head-to-tail” method. You draw one vector, then draw the second vector with its tail on the head of the first. The next vector would be drawn with its tail on the head of the second and so on. The final answer, known as the resultant vector, is found by drawing a vector form the tail of the first vector to the head of the last.
It makes no difference in what order you add the vectors as you can see by the drawing below.
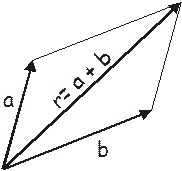
You will not be required to add vectors graphically – it’s a lot of trouble and not very accurate and there are better ways to do it. Here are some other examples.
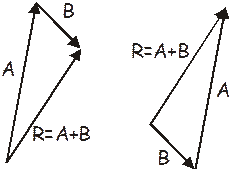

So how do we go about doing this? Well, fugidaboutit. It’s way too much trouble. You need to measure things super accurately, draw angles precisely, &tc. This is all very tedious stuff. It’s far easier to add them utilizing other, better methods. Thus we will not use the head to tail thing.
Here’s what you should be able to do with the head to tail bit: you should be able to make a rough drawing of the vector addition. This is very useful because it will give you an idea of what the approximate direction and magnitude of the resultant vector ought to look like.
Trigonometry: So how do we solve vector problems? Well, gosh, thanks for asking. Here’s how we do the thing - we use trigonometry!
Actually, you’re going to get to use a heck of a lot of trigonometry in this course, you lucky devil.
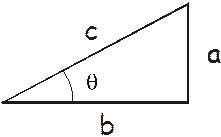
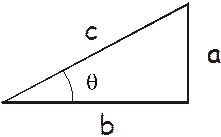
Here is a right triangle. A right triangle has a ninety-degree angle (called a right angle) in it.
In reference to angle q, side a is called the opposite side (it is farthest away from the angle), side b is called the adjacent side (it is “adjacent” to the angle, i.e., right next to it), and side c is called the hypotenuse.
Any two right triangles that have the same interior angle q are similar and the ratios of the sides are a constant (you will, it is to be hoped, recall this from your old geometry class). Observe the drawing below:
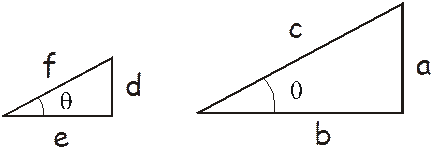
The ratios for the sides of the two triangles is:
![]()
This is what trigonometry is based upon – the ratio of the sides of similar triangles. We will be using three trigonometry functions, that is, three ratios; the sine, cosine, and tangent.
These functions are defined as:
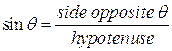

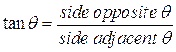
For our original triangle:
![]()
![]()
![]()
- A plane travels east 535 km, then flies north, then flies back to its takeoff point a distance of 718 km. (a) How far north did it travel? (b) What is the angle q ?

(a) A simple way to find the distance the plane traveled north would be to use the Pythagorean theorem.
![]() solve for a:
solve for a:
![]()
(b) To find the angle we can use the tangent function (opposite side over adjacent side):
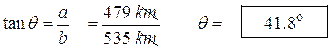
This is actually a vector problem – it may be your very first vector problem. Wow! Don’t you feel all warm and fuzzy inside?
Vector Components: Any vector can be drawn as the resultant of two perpendicular vectors, one along the x axis and the other along the y axis. The two vectors are perpendicular to each other and are called component vectors. Turning a single vector into two component vectors is called “resolving the vector into its x and y component vectors”. This is done using trigonometry. Here’s an example:

Vector A is the one we start with. It is made up of two vectors that lie in the x and y plane. We call the one along the x axis “Ax” and the one along the y axis is “Ay”. Using trig we see that:
![]()
![]()
The angle ![]() can also be easily found:
can also be easily found:
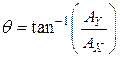
- A ball is thrown with a velocity of 22.5 m/s at an angle of 23.0° to the horizon. What are its vertical and horizontal velocity components?
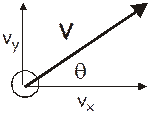

The components look like this:
Using trig to solve the thing we get:


More Vector Problems:
- A velocity vector has the following components: vy is 12.4 m/s and vx is 15.4 m/s, find the angle q.
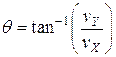
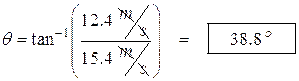
 A boat is traveling north directly across a river that is 5.0 km across. The current is to the east at 3.0 km/h. The boat travels at 5.0 km/h. (a) What is the boat’s resultant velocity? (b) How long does it take to cross the river? (c) How far down the bank does it drift before it reaches the far side?
A boat is traveling north directly across a river that is 5.0 km across. The current is to the east at 3.0 km/h. The boat travels at 5.0 km/h. (a) What is the boat’s resultant velocity? (b) How long does it take to cross the river? (c) How far down the bank does it drift before it reaches the far side?
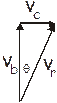 (a) Here is a vector addition drawing, it gives one a basic idea of what the answer looks like.
(a) Here is a vector addition drawing, it gives one a basic idea of what the answer looks like.
F
irst we find resultant velocity: ![]()
![]()
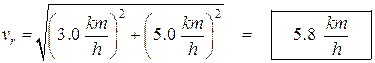
- Find the time to cross: the velocity component that is in the direction to cross the river determines how quickly the boat crosses, so use
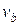 .
.
![]()
![]()
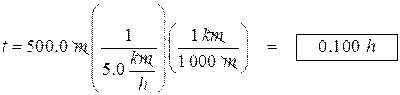
(c) Find distance in horizontal direction:
Ridiculous Trivia:
- In Irian, Java there is a tribe of tall, white people who use parrots as a warning alarms for intruders.
- In Washington D.C., no building can be built taller than the Washington Monument.
- It costs $7 for parking at Universal Studios in Hollywood.
- Levan, which is located in Utah, got its name from ""navel"" which is levan spelt backwards. It was named this because it is in the center of Utah.
- The Liberace Museum in Las Vegas has a mirror-plated Rolls Royce; jewel-encrusted capes, and the largest rhinestone in the world, weighing 59 pounds and almost a foot in diameter.
- Los Angeles's full name is El Pueblo de Nuestra Senora la Reina de los Angeles de Porciuncula --and can be abbreviated to 63% of its size: L.A.
- Maine is the toothpick capital of the world.
- New York's Central Park is nearly twice the size of the entire country of Monaco.
- Since the 1930’s the town of Corona, California has lost all 17 of the time capsules they originally buried.
- The CN Tower, in Toronto, is the tallest freestanding structure in the world with a height of about 553 metres.
- The Golden Gate Bridge was first opened in 1937.
- The Grand Canyon was not seen by a white man until after the Civil War. It was first entered on May 29,1869, by the geologist John Wesley Powell.
- The highest major highway in England is the M62 that connects Liverpool to Hull. At its peak it reaches 1221 feet above sea level.
- The largest ketchup bottle in the world is a 170 feet tall and is located in Collinsville, Illinois, USA. It was built in 1949 by the W.E. Caldwell Company as a water tower.
- The largest school in the world is City Montessori School in India which has over 25,000 students in grade levels ranging from kindergarten to college.
- The Library of Congress, located in Washington D.C., is the largest library in the world.
- The Mall of America, located in Bloomington, Minnesota is so big that it can hold 24,336 school buses.
- The oldest university in the U.S. is Harvard.
- The only flying saucer launch pad in the world is located in St. Paul, Alberta, Canada.
- The proposed William Jefferson Clinton Presidential Library will have a section where you must be 18 or older to read certain documents.
- The San Francisco Cable cars are the only mobile National Monuments.
- The Sears Tower consists of nine framed tubes, which connects nine skyscrapers as one building.
- There are more than 10 million bricks in the Empire State Building.
- The tallest freestanding sculpture in the world is Chief Crazy Horse in South Dakota, USA.
- Three Mile Island is only 2.5 miles long.
Source : http://teachers2.wcs.edu/high/bhs/mikek/AP%20Physics%20Course%20Notes/Kinematics/3%20-%20Vectors.doc
Web site link: http://teachers2.wcs.edu
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Vectors
Vectors
Vectors
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Vectors mean ? Which is the meaning of Vectors?
Vectors physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us