Vectors and scalars
Vectors and scalars
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Vectors and scalars
A Scalar Quantity is one which has magnitude only. Examples: length, area, energy, time.
A Vector Quantity is one which has both magnitude and direction. Examples: displacement, acceleration, force.
Vectors can be represented on a diagram by an arrow, where the vector is in the same direction as the quantity it is representing.
Composition (addition) of two perpendicular vectors
- When adding two vectors, they should be arranged tail-to-tail (the arrow represents the head) and the rectangle should then be completed.
- The resultant is the line joining the two tails to the opposite corner.
- The direction is from the tails to the opposite corner.
- Mathematically, the length of the vector can be found by using Pythagoras’ Theorem.
- Mathematically, the angle can be found by using Tan q = Opp/Adj.
Experiment: To find the Resultant of Two Forces
Attach three Newton Balances to a knot in a piece of thread.
- Adjust the size and direction of the three forces until the
knot in the thread remains at rest.
- Read the forces and note the angles.
- The resultant of any two of the forces can now be shown to be
equal to the magnitude and direction of the third force.
Resolving a vector into two perpendicular Components
You have just seen that two perpendicular vectors can be added together to form a resultant.
Well let’s say we started off with the resultant. Would we be able to get back the two original vectors?
First we need to remember that for a right-angled triangle:
Sin q = Opposite/Hypothenuse, therefore Opposite = Hypothenuse x Cos q {Opp = H Sin q}
Cos q = Adjacent/Hypothenuse, therefore Adjacent = Hypothenuse x Cos q {Adj = H Cos q}
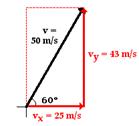
Example
Consider a velocity vector representing a velocity of 50 ms-1, travelling at an angle of 600 to the horizontal:
The Opposite is equal to H Sin q, which in this case = 50 Cos 600 = 43 ms-1.
The Adjacent is equal to H Cos q, which in this case = 50 Sin 600 = 25 ms-1.
Now look over problem 4 and 5, page 86. Then try questions 1 – 4, page 87, followed by questions 7 and 8, page 88.
Leaving Cert Physics Syllabus: Vectors and Scalars
Content |
Depth of Treatment |
Activities |
STS |
|
|
|
|
Vectors and Scalars |
Distinction between vector and scalar quantities. |
|
Vector nature of physical quantities: everyday examples. |
|
|
|
|
|
Composition of perpendicular vectors. |
Find resultant using newton balances or pulleys. |
|
|
|
|
|
|
Resolution of co-planar vectors. |
Appropriate calculations. |
|
What do you get if you cross a mosquito with a rock climber?
You can't cross a vector with a scalar!
Boom Boom!
Exam questions
- [2003]
Give the difference between vector quantities and scalar quantities and give one example of each.
- [2006 OL]
Force is a vector quantity. Explain what this means.
[2003]
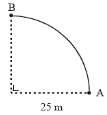
A cyclist travels from A to B along the arc of a circle of radius 25 m as shown.
- Calculate the distance travelled by the cyclist.
- Calculate the displacement undergone by the cyclist.
- [2004]
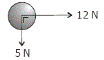Two forces are applied to a body, as shown. What is the magnitude of the resultant force acting on the body?
- [2003]
Describe an experiment to find the resultant of two vectors.
Exam solutions
- A vector has both magnitude and direction whereas a scalar has magnitude only.
- A vector is a quantity which has magnitude and direction.
- The displacement is equivalent to one quarter of the circumference of a circle = 2πr/4 = 25π/2
= 12.5π = 39.3 m.
- Using Pythagoras: x2 = 252 + 252 Þ x = 35.3 m. Direction is NW
- R2 = F12 + F22 Þ R2 = 52 +122
R = 13 N
The marking scheme didn’t look for direction, but it should have, particularly since this is a vectors question and force is a vector. q = tan-1 (5/12).
- Attach three Newton Balances to a knot in a piece of thread.
- Adjust the size and direction of the three forces until the
- knot in the thread remains at rest.
- Read the forces and note the angles.
- The resultant of any two of the forces can now be shown to be
equal to the magnitude and direction of the third force.
Source : http://www.thephysicsteacher.ie/LC%20Physics/Student%20Notes/8.%20Vectors%20and%20Scalars.doc
Web site link: http://www.thephysicsteacher.ie
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Vectors and scalars
Vectors and scalars
Vectors and scalars
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Vectors and scalars mean ? Which is the meaning of Vectors and scalars?
Vectors and scalars physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us