Waves
Waves
The following text is used only for teaching, research, scholarship, educational use and informative purpose following the fair use principles.
We thank the authors of the texts and the source web site that give us the opportunity to share their knowledge
Physics
Waves
The speed of sound is 340 m s-1
The speed of light is 3 × 108 m s-1
A Wave is a means of transferring energy from one place to another
Transverse waves
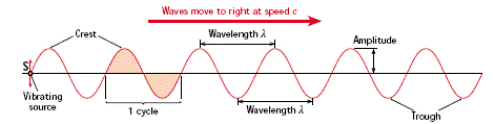
A Transverse wave is a wave where the direction of vibration is perpendicular to the direction in which the wave travels.
Examples
- Light waves.
- Radio waves.
- Waves on a rope.
- Water waves.
Longitudinal Waves
A Longitudinal Wave is a wave where the direction of vibration is parallel to the direction in which the wave travels.
Examples
- Sound waves in a solid, liquid or gas.
- Compression waves on a spring.
Terms used to describe a wave
The wavelength of a wave is the distance from one point on the wave to the corresponding point on the next cycle.
The frequency of a wave is a measure of the number of oscillations (vibrations) of the wave per second*.
The periodic time of a wave (T) is the time taken for one complete cycle.
Variable |
Symbol |
Unit |
Symbol for unit |
Frequency |
f |
Hertz |
Hz |
Wavelength |
l (“lamda”) |
metres |
m |
Velocity |
v (or c for light) |
metres/second |
m/s |
Periodic Time |
T |
second |
s |
Relationship between frequency, velocity and wavelength |
Relationship between Periodic Time and frequency* |
|
T = 1/f |
See Worked Problems 1 – 4, page 178, then try Questions 1 – 7, 9 - 11 (page 178/179).
Characteristics of a wave
- Reflection is the bouncing of waves off of an obstacle in their path.
- Refraction is the changing of direction of a wave as it travels from one medium to another.
Note that when a wave travels from one medium to another its frequency does not change*
- Diffractionis the spreading of waves around a slit or an obstacle.
This effect is only significantly noticeable if the slit width is approximately the same size as the wavelength of the waves*.
- Interference*
Interference occurs when waves from two sources meet to produce a wave of different amplitude.
Constructive Interference occurs when waves from two coherent sources meet to produce a wave of greater amplitude.
(Constructive interference occurs when the crests of one wave are over the crests of another wave).
Destructive Interference occurs when waves from two coherent sources meet to produce a wave of lower amplitude.
(Destructive interference occurs when the crests of one wave are over the troughs of the second wave.
This will happen if one wave is half a wavelength out of phase with respect to the other).
Coherent Waves*: Two waves are said to be coherent if they have the same frequency and are in phase.
“In phase” means crests stay over crests and troughs stay over troughs.
Stationary waves
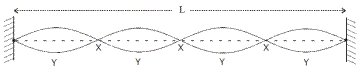Stationary waves are formed when two periodic travelling waves of the same frequency and amplitude, travelling in opposite directions, meet.
From the diagram we can see that:
- The distance between two consecutives nodes is l/2
- The distance between two consecutive antinodes is l/2
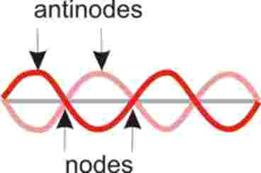The distance between an anti-node and the next node is l/4
(“nodes” = “no” movement)
See problems 5 and 6, page 185, 186. Then try Exercise 16.2, page 186.
The Doppler Effect
The Doppler Effectis the apparent change in the frequency of a wave due to the relative motion between the source of the wave and the observer.
Consider a source S emitting a wave with crests 1, 2, 3 as shown.
The distance between successive crests is the same; therefore the number of crests that pass point A in one second will correspond to the frequency of the wave.
These waves will pass over an observer in equal intervals of time.
This means that the wavelength and therefore the frequency will be the same.
In this case the source is moving to the right while emitting the waves.
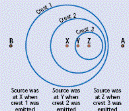
The result is that:
- Ahead of the moving source, the crests are closer together than crests from the stationary source would be. This means that the wavelength is smaller and the frequency is greater.
- Behind the moving source, the crests are further apart than crests from the stationery source would be.
- This means the wavelengths are greater and therefore the frequency is less.
Formula:
f” = apparent frequency
f = actual frequency
c = speed of the wave
u = speed of the moving source
Remember that the sign below the line is minus if the source is moving towards the observer – ‘Minus Is Towards’ (MITS)
Applications of the Doppler effect:
- Police speed traps
- Measuring the red shift of galaxies in astronomy*
- Ultrasound (blood movement or heartbeat of foetus)
- Weather forecasting.
Note:
The noise from a racing car as it approaches and then moves away from an observer is an example of the Doppler effect.
But it is not an application!!
Demonstration of the Doppler effect
The Doppler effect for sound waves is dramatically demonstrated by swinging a ringing tuning fork around your head.
The Doppler Effect – Exam questions
Note that when explaining the effect, the marking scheme looks for four separate points here:
- A series of non-concentric circles.
- Direction of motion of source and position of observer must be indicated.
- Reference to apparent change in wavelength.
- Reference to resulting apparent change in frequency.
Leaving Cert Physics Syllabus
Content |
Depth of Treatment |
Activities |
STS |
|
|
|
|
1. Properties of waves. |
Longitudinal and transverse waves: frequency, amplitude, wavelength, velocity. |
Appropriate calculations. |
Everyday examples, e.g.
|
|
|
|
|
2. Wave phenomena |
Reflection. Refraction. Diffraction. Interference. |
Simple demonstrations using slinky, ripple tank, microwaves, or other suitable method. |
|
|
|
|
|
|
Stationary waves; relationship between inter-node distance and wavelength. |
|
|
|
|
|
|
|
Diffraction effects
with reference to significance of the wavelength. |
|
|
|
|
|
|
3. Doppler effect |
Qualitative treatment. |
Sound from a moving source. |
Red shift of stars. |
Extra Credit
Earthquakes and Waves
Earthquakes and violent volcanic eruptions are a source of seismic waves that result in planet Earth ringing like a bell for quite some time (up to weeks) after the "striking" event.
Less dramatically, the Earth "hums" all of the time with a collection of frequencies in the 1 to 10 mHz range.
This frequency translates into a period of typically 200s, which gives a clue to its origin.
Many sea-borne waves near to continental land masses (infragravity waves) have periods of this order of magnitude.
It is the interaction of these waves in the shallower water over continental shelves with the seabed that drive the "hum".
Most sea waves originate in the action of winds over the water surface.
In their turn winds derive their energy from the Sun's unequal heating of the Earth's surface and atmosphere.
So the Earth is humming to the tune of the Sun.
*The frequency of a wave is a measure of the number of oscillations (vibrations) of the wave per second.
Another way of defining frequency of a wave is to say it is the number of waves that pass a fixed point per second.
This second definition is helpful in explaining the next point: T = 1/f
*Relationship between Periodic Time and frequency
T = 1/f or f = 1/T
If three waves pass a fixed point per second (f = 3 Hz), it follows that the time for one wave to pass (periodic time T)
is 1/3 (seconds).
Alternatively if the Periodic Time (T) is 1/5 seconds, it follows that five waves will pass in one second (f = 5 Hz).
*When a wave travels from one medium to another its frequency does not change
Basically if a wave ‘wobbles’ so many times a second in air, and then comes in contact with another medium e.g. water, the water will ‘wobble’ (move in and out) in sympathy with the driving force, and therefore at the same frequency.
The speed however will change, and because speed is directly proportional to wavelength (from v = fl), if the speed of the wave were to double (and the frequency remains constant) then the wavelength would double also.
*Diffractionis the spreading of waves around an obstacle
This effect is only significantly noticeable if the slit is approximately the same size as the wavelength of the waves.
So if the slit width is of the order of cm to metres, then sound may well be noticeably diffracted, depending on the frequency of the sound, because the corresponding wavelength may well be similar to the slit width.
However the same will not happen for light, because the wavelength for light is of the order of 10-7 metres, which doesn’t correspond to slits that one encounters every day.
There are objects which are specifically designed to have these slit widths specifically so that light will diffract after passing through them. These are called ‘Diffraction Gratings’ and we will use them when studying Chapter 18: The Wave Nature of Light.
Similarly, compact dics have grooves in them which are approximately the same width as the wavelength of light, so shining white light on a CD gives a nice spectral pattern!
So why is the effect only noticeable when the wavelength is the same size as the gap?
Answer: I don’t know. If you can explain it or find someone else who can, please get back to me. I suspect it is another of those concepts which is a lot more technical than it first appears. But then maybe I just think that to make me feel better J
*Interference
Interference is considered to be the most significant of the four characteristics because if a form of energy undergoes interference then it must be a wave (as opposed to travelling as particles). We know that both sound and light travel as waves because we can show that they undergo interference.
*Coherent Waves
Strictly speaking the definition is a little more convoluted:
Two waves are said to be coherent if they have the same frequency (or wavelength) and are in phase (or have a constant phase difference between them)
Another necessary condition (for waves to be coherent) is therefore that both waves travel at the same speed.
*Applications of the Doppler effect: Measuring the red shift of galaxies in astronomy
Strictly speaking the red-shift is due to two separate factors; other galaxies moving away from us and the fact that the space itself is expanding (our universe is expanding), so the distance between crests is increasing and this would happen even if the galaxies were not speeding away from us.
Exam questions
Speed of sound = 336 m s-1
Speed of light = 3 × 108 m s-1
- [2007 OL][2010 OL]
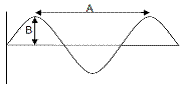The diagram shows the waveform of a musical note.
What is the name given to (i) the distance A, (ii) height B?
- [2007 OL][2010]
Explain what is meant by the frequency of a wave.
- [2005 OL]
What is meant by the amplitude of a wave?
- [2005][2006 OL]
Explain the difference between longitudinal and transverse waves.
- [2005 OL]
A wave motion has a frequency of 5 hz and a wavelength of 200 m. Calculate the speed of the wave.
- [2007 OL]
A tin-whistle produces a note of 256 Hz. Calculate the wavelength of this note.
- [2010 OL]
If the natural frequency of a string is 250 Hz calculate the wavelength of the sound wave produced.
- A mobile phone transmits at 1200 MHz from its antenna.
Calculate the length of its antenna, which is one quarter of the wavelength that it transmits.
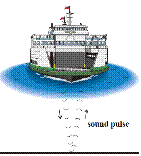[2006 OL]- A ship detects the seabed by reflecting a pulse of high frequency sound from the seabed. The sound pulse is detected 0.4 s after it was sent out and the speed of sound in water is 1500 m s–1.
Calculate the time taken for the pulse to reach the seabed.
- Calculate the depth of water under the ship.
- Calculate the wavelength of the sound pulse when its frequency is 50 000 Hz.
- [2004 OL][2002 OL][2005 OL][2009]
Explain the term diffraction.
- [2004 OL][2005 OL]
Explain the term interference.
- [2008]
Why does diffraction not occur when light passes through a window?
- [2006]
A sound wave is diffracted as it passes through a doorway but a light wave is not. Explain why.
- [2002]
Explain the term constructive interference.
- [2002]
Explain the term coherent sources.
- [2007]
What is the condition necessary for destructive interference to take place when waves from two coherent sources meet?
- [2004 OL]
- The diagram shows a stationary wave (standing wave) on a vibrating stretched string.
What is the name given to the points on the string marked (i) X, (ii) Y?
- How many wavelengths are contained in the distance marked L?
- A note of wavelength 1.4 m is produced from a stretched string. If the speed of sound in air is 340 m s−1, calculate the frequency of the note.
- [2006]
A stretched string of length 80 cm has a fundamental frequency of vibration of 400 Hz.
What is the speed of the sound wave in the stretched string?
- [2005]
The diagram shows a guitar string stretched between supports 0.65 m apart.
The string is vibrating at its first harmonic. The speed of sound in the string is 500 m s–1.
What is the frequency of vibration of the string?
- Draw a diagram of the string when it vibrates at its second harmonic.
- What is the frequency of the second harmonic?
- [2007]
- Radio waves of frequency 30 kHz are received at a location 1500 km from a transmitter.
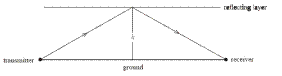The radio reception temporarily “fades” due to destructive interference between the waves travelling parallel to the ground and the waves reflected from a layer (ionosphere) of the earth’s atmosphere, as indicated in the diagram.
Calculate the wavelength of the radio waves.
- What is the minimum distance that the reflected waves should travel for destructive interference to occur at the receiver?
- The layer at which the waves are reflected is at a height h above the ground.
Calculate the minimum height of this layer for destructive interference to occur at the receiver.
The Doppler Effect
- [2008 OL]
The pitch of a note emitted by the siren of a fast moving ambulance appears to change as it passes a stationary observer. Name this phenomenon.
- [2008][2007][2006][2003][2002][2010]
What is the Doppler Effect?
- [2010]
Describe a laboratory experiment to demonstrate the Doppler effect.
- [2007][2003][2008 OL][2010]
Explain, with the aid of labelled diagrams, how the Doppler Effect occurs.
- [2002 OL]
Give an example of the Doppler Effect.
- [2008][2003][2004 OL][2007 OL]2008 OL][2010]
Give two applications of the Doppler Effect.
- [2010]
What causes the red shift in the spectrum of a distant star?
- [2005]
It is noticed that the frequency of the received radio signal changes as the satellite orbits Saturn. Explain why.
- [2008]
A rally car travelling at 55 m s–1 approaches a stationary observer. As the car passes, its engine is emitting a note with a pitch of 1520 Hz. What is the change in pitch observed as the car moves away?
- [2003]
- Bats use high frequency waves to detect obstacles. A bat emits a wave of frequency 68 kHz and wavelength 5.0 mm towards the wall of a cave. It detects the reflected wave 20 ms later.
Calculate the speed of the wave.
- If the frequency of the reflected wave is 70 kHz, what is the speed of the bat towards the wall?
- [2010]
The yellow line emitted by a helium discharge tube in the laboratory has a wavelength of 587 nm.
The same yellow line in the helium spectrum of a star has a measured wavelength of 590 nm.
- What can you deduce about the motion of the star?
- Calculate the speed of the moving star.
- [2007]
- The red line emitted by a hydrogen discharge tube in the laboratory has a wavelength of 656 nm.
The same red line in the hydrogen spectrum of a moving star has a wavelength of 720 nm.
Is the star approaching the earth? Justify your answer.
- Calculate the frequency of the red line in the star’s spectrum
- Calculate the speed of the moving star
Exam Solutions
- A = wavelength
B = amplitude
- The frequency of a wave is the number of waves passing a fixed point per second.
- Amplitude corresponds to the height of the wave.
- A Transverse wave is a wave where the direction of vibration is perpendicular to the direction in which the wave travels.
A Longitudinal Wave is a wave where the direction of vibration is parallel to the direction in which the wave travels.
- c = f λ Þ c = 5 × 200 = 1000 m s-1.
- The speed of sound in air is 340 m s−1
c = fλ Þλ = c/f Þ λ = 340/256 = 1.33 m.
- v = f λ
λ = v/f
λ = 340/250
= 1.36 m
- λ = c/f
λ = (3 × 108)/(1.2 × 109)
λ = 0.25 m
Length of antenna = 0.25/4 = 0.0625 m.
- 0.2 s.
- v= s/t Þ s = v × t Þ s = 1500 × 0.2 = 300 m.
- c = fλ Þ λ = c/f Þ λ = 1500/50000 = 0.03 m.
- Diffractionis the spreading of waves around a slit or an obstacle.
- Interference occurs when waves from two sources meet to produce a wave of different amplitude.
- The window is too wide (relative to wavelength of light).
- Diffraction only occurs when the width of the gap is approximately equal to the wavelength of the wave. This is the case for a sound wave but the wavelength of a light-wave is very small compared to the size of a doorway.
- Constructive Interference occurs when waves from two coherent sources meet to produce a wave of greater amplitude.
- Two waves are said to be coherent if they have the same frequency and are in phase.
- They must be out of phase by half a wavelength (this means that the crest of one wave will be over the trough of the other.
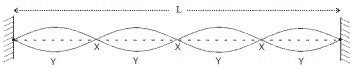X = node, (ii) Y = antinode- Answer: 2
- c = fλ Þ 340 = f × 1.4 Þ f = 242.9 Hz
- v = f λ Þ v = 400(1.6) = 640 m s-1
- λ = 2 × 0.65 = 1.3 m
v = fλ Þ f = v/ λ = 500 / 1.3 Þ f = 384.6 Hz
See diagram- f2nd = 2f1st = 769.2 Hz
- c = f λ Þ λ = c/f = (3.0 × 108)/ (30000) = 104 m = 10 km
- For destructive interference to occur the reflected wave must arrive out of phase, i.e. it must have travelled half a wavelength more than the regular wave.
The regular wave will have travelled 1500 km and half a wavelength is 5 km therefore the reflected wave must travel1500 km + 5 km = 1505 km.
- Use Pythagoras: h = 61000 m
The Doppler Effect
- The Doppler effect.
- Attach a string to a buzzer.
Swing the buzzer over your head.
An observer will note a frequency change as the buzzer approaches then recedes from source the observer.
- The Doppler Effectis the apparent change in the frequency of a wave due to the relative motion between the source of the wave and the observer.
- Non-concentric circles labelled as waves
Source and direction of motion (stated/implied)
Position of observer indicated
Close parts of circles show short wavelength
Shorter wavelength implies higher frequency on approaching observer (or vice versa)
- The pitch of an ambulance changes as it goes past.
- Distant stars are moving away from us therefore the wavelengths increase.
- Calculate speeds of stars or galaxies, speed traps.landing aircraft, ultrasound (blood movement or heartbeat of foetus), weather forecasting.
- Doppler Effect due to relative motion between source of signal and the detector
Þ 
Þ f1 = 1308.35 Hz
Þ change in frequency = 1520 – 1308.35 = 211.65 Hz.
- The star is moving away from earth
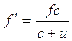
Substitution: c = 3 × 108, f = 5.11073 × 1014 and f’ = 5.08475 × 1014
Answer: u = 1.53 × 106 m s-1
- v = fλ = 68000 ×.005 = 340 m s-1
- f ' = fc / c± u
70000 = (68000)(340)/340 - u
u = 9.7 m s-1
- No; the wavelength has increased therefore it must be moving away.
- f’ = c / λ’
f’ = 3×108/720×10-9 Þ f’ = 4.17 × 1014 Hz
- Formula: f’ = fc/c+u
Substitution: 4.17 ×1014 = (4.57 ×1014)(3 ×108) / (3.00×108 + u)
Answer: u = 2.92 × 10 7 ms-1
Source : http://www.thephysicsteacher.ie/LC%20Physics/Student%20Notes/16.%20Waves.doc
Web site link: http://www.thephysicsteacher.ie
Author : not indicated on the source document of the above text
WAVES
The class, this AP Physics thing, has been terrific so far, hasn’t it? Motion and mechanical energy were awesome were they not?
It’s time to build on the energy thing and keep the excitement moving along. This will surely happen with our next topic – WAVES. Waves turn out to be one of the ways that energy can be transferred from one place to another.
Out at sea, the waves roll on.
Waves º disturbances that travel through space transferring energy from one place to another.
Sound, light, and the ocean's surf are all examples of waves.
There are two species of waves, mechanical waves and electromagnetic waves. Mechanical waves require a medium that the wave will then travel through, or rather, the disturbance will travel through. Electromagnetic waves do not require a medium. The disturbance that travels is a changing magnetic and electric field (both of which you, lucky student, will get to study in the near future). We’ll examine these waves later on in the course.
A key concept here is that the only things that moves is the disturbance. The medium itself does not move.
That waves carry energy should be obvious. Picture the waves on the ocean. Waves are generated far out at sea mainly by the wind. The wave travels through the water for hundreds or even thousands of miles. Finally it reaches the shore where the waves pound against the beach. They have enough energy to break down the coastline and erode away continents.
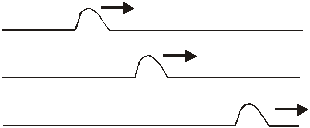
Traveling Waves: The traveling wave is a sort of bump that travels through a medium. A good example of a traveling wave would be a pulse sent down a rope. Such a thing is shown in the drawing below.
Note that the rope itself does not travel, just the pulse, which is the disturbance.
You will have seen traveling waves in one of the class demonstrations on a long slinky spring.
Another type of wave is the continuous wave. Sometimes these are called wave trains. A continuous wave requires a periodic source of energy and a medium for the wave to travel through.
There are two types of mechanical waves, the transverse wave and the longitudinal wave.
Transverse Wave - The disturbance direction is perpendicular to the wave direction
Longitudinal Wave - The disturbance direction is parallel to the wave direction
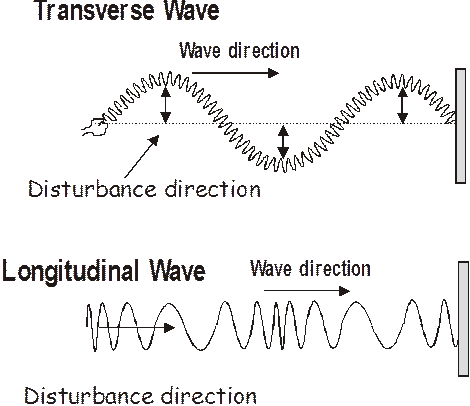
The Physics Kahuna will have shown you a lovely demonstration of these two types of waves. Here are some examples of these waves:
Transverse waves – water waves, waves on a string or spring, seismic waves, and electromagnetic waves.
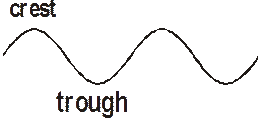Longitudinal waves – well, the best example would be sound waves, but you saw them on springs as well.
A transverse wave is made up of a series of positive pulse and negative pulses. The positive pulses are called crests and negative pulses are called troughs. The height of the crest and the depth of the trough is of course the amplitude of the wave.
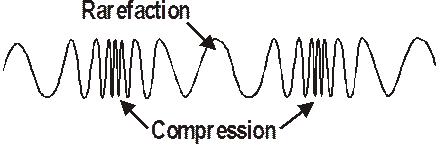
Longitudinal waves are a bit different. Basically the medium gets scrunched or pushed together and then pulled apart – stretched out The areas of increased medium density are called compressions. The compression is surrounded on either side by an area where the medium is stretched out. These areas of low medium density are called rarefactions.
A really important, like key-type concept is that it is only the disturbance that moves, not the medium. Take you your basic water waves for example. These waves can travel hundreds of miles across the sea. But only the wave travels. The disturbance in water waves is the changing height of the water – the water goes up and it goes down. A duck sitting on the water would not be swept forward with the wave. Instead the duck would bob up as the crest of the wave passed beneath it and then the duck would go down as the trough went past. The Physics Kahuna has made a sequential type drawing of the very thing.
The frequency of a traveling wave is simply the number of cycles divided by the time they occur within (or something that sounds more scientific than that, the old Physics Kahuna is stretching – at the limits of his writing skills).
Here f is the frequency, n is the number of cycles (and has no unit) and t is the time.
- A speed boat zooms by you as you lie on your floating mattress. You find yourself bobbing up and own on the waves that the boat made. So, you decide to do a little physics experiment. You count the waves and time how long it takes for them to go past. Six wave crests go by in five seconds. So what is the frequency?
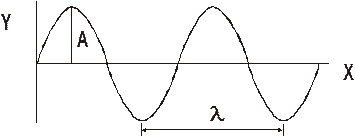
Below is the plot of a transverse wave. The displacement is plotted on the y axis and distance is plotted on the x axis. The amplitude, A, is shown. This is the maximum displacement, just as it was for periodic motion. The other thing that is shown on the graph is the wavelength, l. The wavelength is the distance between two in phase points on the wave.
The wave is traveling at some velocity v. We know that velocity is given by this equation:
We also know that the wave travels a distance of l in the period, T.
We can plug these into the equation for velocity:
But we also know that the period is given by:
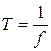so
We can plug this in for T in the velocity equation we’ve been working on:
This gives us a very important equation:
- A middle C note (notes are these musical frequency kind of deals) has a frequency of approximately 262 Hz. Its wavelength is 1.31 meters. Find the speed of sound.
- A wave has a frequency of 25.0 Hz. Find the (a) wavelength, (b) period, (c) amplitude, and (d) velocity of wave. A graph of this wave is shown below.
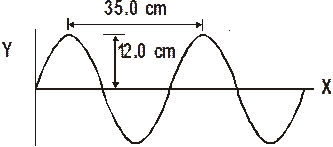
(a) Amplitude: We can read the amplitude directly from the graph: 
(b) Wavelength: This can be read directly from the graph as well. 
(c) Period: The period is the inverse of the frequency, which we know.
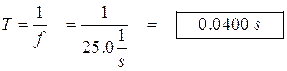
(d) Velocity: We use the wave velocity equation.
Here’s another problem.
- The speed of light is 3.00 x 108 m/s. What is the wavelength for an FM radio signal broadcast at 105.3 MHz? (Note, radio waves all travel at the speed of light.)
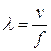
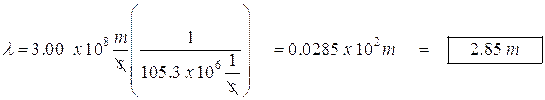
Wave Dynamics: When a wave is busy t raveling through a medium, it’s a beautiful thing. But what happens when a wave travels from one medium to another? What happens when two waves meet up? These are good questions and the answers are even better.
Reflection: When a wave traveling through a given medium encounters a new medium, two things happen: some of the energy the wave is carrying keeps going on into the new medium and some of the wave energy gets reflected back from whence it came. If the difference in the wave velocity is large, then most of the wave will be reflected. If the difference in velocity is small, most of the wave will be transmitted into the new medium. The junction of the two mediums is called a boundary.
If there is no relative motion between the two mediums, the frequency will not change on reflection. Also, and this is a key thing, the frequency does not change when the wave travels from one medium into another. It stays the same. This means that the wavelength does change.
 |
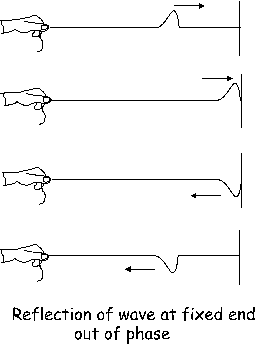There are two types of reflection. The type of reflection depends on how the mediums at the boundary are allowed to move. The two types are: fixed end reflection, and free end reflection.
For fixed end reflection think of the medium as being constrained in its motion. In the picture to the left you see a string that is securely fixed to the wall. The string (the old medium) is free to move up and down, but at the boundary where it meets the new medium (the wall) it is constrained – the string can’t really move up and down like it could before. In fixed end reflection, the wave that is reflected back is out of phase by 180°. In the drawing you see an erect pulse traveling down the string. When it is reflected it ends up inverted. It will have the same speed going in as coming out. So in fixed end reflection an erect pulse would be reflected as an inverted pulse.
|
In free end reflection, the medium is free to move at the boundary. The reflected wave will be in phase. In the drawing on the right, you see an erect pulse traveling into the boundary being reflected with no phase change. The pulse went in erect and came out erect. Water waves reflecting off a solid wall are a good example of free end reflection.
Wave Speed: For a wave on a string, the speed of the wave is directly proportional to the tension in the string. Increase the tension and the wave velocity will increase.
The speed of sound waves in air is directly proportional to air temperature and directly proportional to the air density. In other words, as the temperature of the air increases, the speed of sound increases. As the density of the air increases, the speed of sound also increases. For a given air temperature, the speed of sound would be less in Gillette than it is in Orlando because the air is less dense in Gillette than in Orlando due to the greater altitude of our fair city.
|
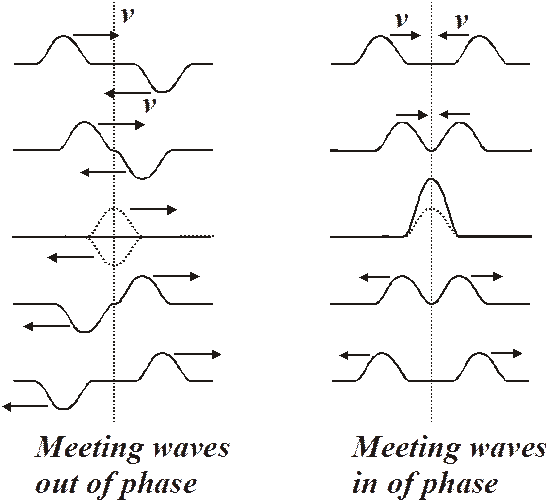
Principle of Superposition: What happens when two or more waves encounter each other as they travel through the same medium? The waves can travel right through each other. As they do this, they add up algebraically to form a resultant wave.
Toss a pebble in a pond and it makes a series of waves that spread out in expanding circles. You can see a drawing of the resultant wave pattern from such an event the waves travel outward in a series of expanding wave fronts. In the drawing, each of the dark lines represents a wave crest. As the wave front expands, the energy of the wave gets spread out and the wave crest decreases in amplitude. Eventually the energy is so spread out and diluted that the wave will cease to exist. This decrease in amplitude from spreading is called dampening or attenuation. This is why you couldn’t hear your mom calling you home when you were a wee tyke several blocks away.
What happens when two pebbles hit the water? Both produce waves and where the waves meet they produce interference patterns.
Here is a drawing showing a set of interference patterns from the two pebbles in the water deal.
These interference patterns occur where the wave crests and troughs meet each other. The interactions behave according to the law of superposition
Law of superposition º when 2 or more waves meet, the resulting displacement is the algebraic sum of the individual separate wave displacements.
These interference patterns will be of great importance later on when we study light.
Basically, the waves add up or cancel each other out. Waves can add up constructively - we get constructive interference, or they can add up destructively - destructive interference.
Where two crests meet, they add up to make an even larger crest. Where a crest and a trough meet, they add up destructively - subtract from each other. So if a wave meets another wave that has the same amplitude but is out of phase (crest to trough, so to speak) they will completely cancel each other out.
Standing waves: If you take a long, slinky spring and fix one end of it to a wall and then shake the free end you produce a pulse that travels down the spring. The pulse will be reflected when it reaches the end of the spring. This would be fixed end reflection so it would be out of phase. If you just wave the end of the spring up and down, you get a very confused, chaotic looking thing. But, if you wave the end of the spring at just the right frequency, you can produce a standing wave. You produce an incident wave that travels down the rope. If the frequency is the correct value, the incident wave and the reflected wave will alternately interfere with each other constructively and destructively. The effect is that parts of the spring will not move at all and other parts will undergo great motion.
The two waves moving in opposite directions will form a standing wave. The law of superposition acts and we get constructive and destructive interference, which forms the standing wave.
You will have observed standing waves in class with some of the demonstrations that we did. The parts of the wave that don't seem to be doing much are called the nodes and the places where the wave is undergoing maximum movement are called antinodes. The end of a string with such a wave that is attached to the wall would have to be a node, would it not?
You can produce a variety of standing waves by controlling the frequency of the wave. You will have seen a delightful demonstration of standing waves in action.
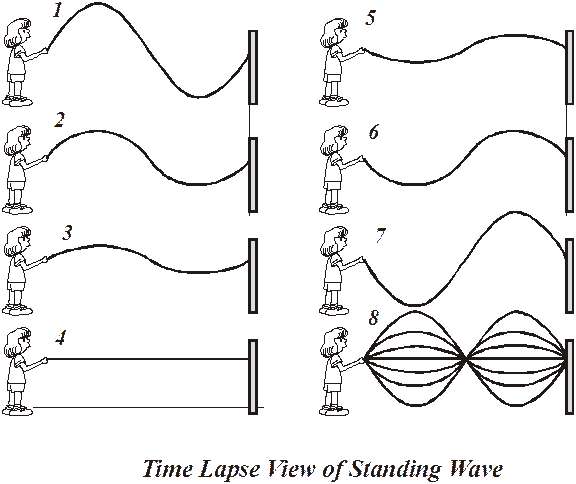
Musical instruments produce standing waves. Piano strings, the interior of a tuba, a flute, and violin strings all produce standing waves. Buildings being buffeted about by the wind also have standing waves. Both transverse waves and longitudinal waves can form standing waves.
|
The standing wave to the left represents one half of the wavelength of the wave or ½ l.
This would be a complete wave cycle or 2/2 l or 1 l.
This would be 3/2 l or 1 ½ wave.
The lowest frequency standing wave for a system is called the fundamental frequency or the first harmonic.
Fundamental Frequency º Lowest frequency of vibration
Integer multiples of the fundamental frequency are called harmonics. The first harmonic is the fundamental frequency. The second harmonic is simply two times the fundamental frequency. The third harmonic is three times the fundamental harmonic. And so on.
Source : http://teachers2.wcs.edu/high/bhs/mikek/AP%20Physics%20Course%20Notes/Waves/2%20-%20Wave.doc
Web site link: http://teachers2.wcs.edu
Author : not indicated on the source document of the above text
If you are the author of the text above and you not agree to share your knowledge for teaching, research, scholarship (for fair use as indicated in the United States copyrigh low) please send us an e-mail and we will remove your text quickly.
Waves
Waves
Waves
This is the right place where find the answers to your questions like :
Who ? What ? When ? Where ? Why ? Which ? How ? What does Waves mean ? Which is the meaning of Waves?
Waves physics notes
Alanpedia.com from 1998 year by year new sites and innovations
Main page - Disclaimer - Contact us